
- •1.Понятие решения задачи мат. Программиров.
- •2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными задачи лп
- •6. Формула приращения целевой функции злп.
- •7. Достаточное условие оптимальности в злп. Достаточное условие неразрешимости злп
- •8. Итерация симплекс–метода
- •11. Нахождение базиса угловой точки. Пример
- •12. Постановка тз. Построение нач. Плана перевозок методом северо-западного угла, методом мин. Элемента.
- •13. Определение закрытой модели тз. Критерий существования решения тз.
- •14. Исследование мн-ва клеток транспортной таблицы
- •15. Достаточное условие минимальности стоимости перевозок
- •16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •17. Метод исключения решения задачи на условный минимум. Пример.
- •18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
- •19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
- •20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
- •21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
- •22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
- •26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
- •27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
- •28.Определение двойственной задачи к задаче математического программирования.
- •29. Связь между двойственной и прямой задачами математического программирования.
- •30.Пример решения задачи оптимизации с помощью теории двойственности
- •31.Основные определения в задаче одномерной минимизации. Примеры.
- •33. Метод золотого сечения решения задачи одномерной минимизации.
- •34. Обоснование метода ломаных решения задачи одномерной минимизации.
- •35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
- •36.Алгоритм метода скорейшего спуска решения змм.
- •37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
- •38.Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
- •39.Сходимость метода скорейшего спуска.
- •41. Метод вариаций Лагранжа
- •42. Уравнение Эйлера
- •43. Случаи интегрируемости ур-ния Эйлера. Примеры.
- •44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
- •46. Задача вариационного исчисления с движущимся по кривой концом.
- •47. Примеры задач динамического программирования, их особенности
- •48.Принципы динамического программирования и функциональные уравнения Беллмана.
33. Метод золотого сечения решения задачи одномерной минимизации.
МЗС позволяет решить задачу с требуемой точностью при меньшем кол-ве вычислений значения функции.
Опр. Золотым сечением отрезка наз деление отрезка на 2 неравные части так, что отношение длины меньшей части к длине большей равно отношению длины большей части к длине всего отрезка.
Т-ки, кот. делят отрезок в золотом отношении
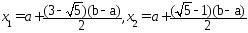
Описание МЗС.
Решаем задачу
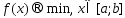 .
Положим а1=а,b1=b
и найдем точки х1 и х2, котор делят [a1;b1]
в золотом сечении. Вычислим
.
Положим а1=а,b1=b
и найдем точки х1 и х2, котор делят [a1;b1]
в золотом сечении. Вычислим
 и
и .
Если
.
Если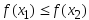 ,
то положим а2=а1,b2=x2,
,
то положим а2=а1,b2=x2,
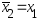 .
Если
.
Если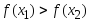 ,
то а2=х1,b2=b1,
,
то а2=х1,b2=b1,
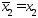 .
Длина построенного отрезка [a2;b2]
равна
.
Длина построенного отрезка [a2;b2]
равна
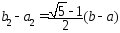 и точка
и точка ,
кот. делит отрезок [a2;b2]
в золотом отношении.
,
кот. делит отрезок [a2;b2]
в золотом отношении.
Пусть на некотор.
этапе найден отр-к
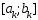 ,
найдены т-ки х1,
,
найдены т-ки х1,
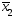 ,…,
,…,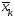 и вычислены значения
и вычислены значения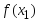 ,f(
,f(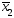 ),…,f(
),…,f(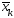 ).
Длина отрезка
).
Длина отрезка
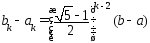 .
И на отрезке
.
И на отрезке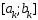 есть т-ка
есть т-ка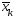 ,
кот. делит этот отрезок в ЗО и в кот.
вычислено значение целевой функции.
,
кот. делит этот отрезок в ЗО и в кот.
вычислено значение целевой функции.
Определим следующ.
т-ку по правилу
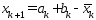 .
.
Предположим, что
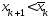 (
( ).
Вычислим знач. ф-ции в т-ке
).
Вычислим знач. ф-ции в т-ке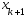 .Если
выполняется неравенство
.Если
выполняется неравенство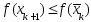 ,
полагаем
,
полагаем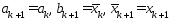 .
Если
.
Если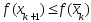 ,
то
,
то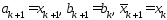 ,
в результате получим отрезок
,
в результате получим отрезок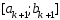 ,
имеющий непустое пересечение с мн-вом
решений задачи, длина кот.
,
имеющий непустое пересечение с мн-вом
решений задачи, длина кот.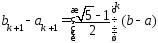
Если количество
вычислений значений целевой ф-ции ничем
не огранич., то процесс вычислений
продолжается до тех пор, пока не будет
выполнятся неравенство
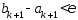
Если количество
вычислений значений целевой ф-ции ничем
огранич., то процесс вычислений
заканчивается, когда будет выполнено
заданное число итераций. В качестве
точки минимума выбираем т-ку
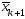 с вычисленным в ней значением целевой
ф-ции.
с вычисленным в ней значением целевой
ф-ции.
Погрешность этого
метода:
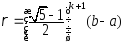
Замечание. Преимуществом МЗС явл. тот факт, что на каждой итерации знач. ф-ции вычисляется только один раз.
Замечание. МЗС можно применять для нахождения минимума функции не являющейся унимодальной. Но в этом случае решение может находиться далеко от глобального минимума.
34. Обоснование метода ломаных решения задачи одномерной минимизации.
Метод ломаных
применяется для решения задачи
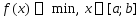 (1),
без требования унимодальности ф-ции f,
но эти ф-ии должны уд. усл. Липшица.
(1),
без требования унимодальности ф-ции f,
но эти ф-ии должны уд. усл. Липшица.
Опр.
Говорят, что ф-ция
 уд.усл. Липшица на [a;b],
если
уд.усл. Липшица на [a;b],
если
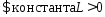 ,
что
,
что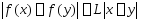
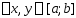 .
(2) Геометрическое усл.Липшица означает,
что угловой коэф-т
.
(2) Геометрическое усл.Липшица означает,
что угловой коэф-т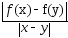 хорд, кот соединяют две произвольные
точки графика ф-цийy=f(x)
не превосходит константы L.
хорд, кот соединяют две произвольные
точки графика ф-цийy=f(x)
не превосходит константы L.
Если ф-я уд.усл. Липшица на [a;b] то она явл-ся непрерывной на [a;b].
Т1: Пусть f(x)-определена и непрерывна на [a;b] и на каждом [ai;ai+1], где а=a1<a2<…<an<an+1=b уд. усл. Липшица с конст Li, тогда f(x)уд. усл Лип на всем отр-ке [a;b]с конст L=maxLi.
Д-во:
выберем произвольные x,y
из отрезка [a,b].
Предположим, что т-ка
 .
.
Рассм.модуль разности
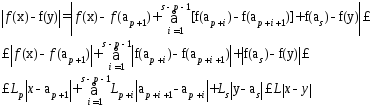
Т2: Пусть f(x)–дифер на [a;b] и её производная огр-на на [a;b], тогда эта ф-ция уд. усл. Лип с конст. L=sup|f’(x)|
Д-во: т.к. ф-ция f(x) диф-ма, то по формуле конечных приращений приращение ф-ции
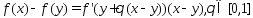
Отсюда и из ограниченности производной следует утв. теоремы.
Пусть ф-я f(x) удовлетворяет на [a;b] условию Липш (2) с константой L. Зафиксируем некоторую точку y из [a;b] и построим ф-цию
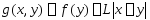 ,
,
 ,
,
g(y,y)=f(y)
![]() .
Ф-ция g
явл. кусочно-линейной ф-цией, ее график
есть ломаная с углами наклона L
(до y)
и –L
(после y)
и в т-ке y
g(y,y)=f(y).
.
Ф-ция g
явл. кусочно-линейной ф-цией, ее график
есть ломаная с углами наклона L
(до y)
и –L
(после y)
и в т-ке y
g(y,y)=f(y).
Рассмотрим
нерав-во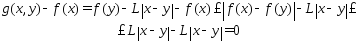 т.е.
т.е.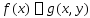 ,
,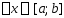 .
.
