
- •1.Понятие решения задачи мат. Программиров.
- •2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными задачи лп
- •6. Формула приращения целевой функции злп.
- •7. Достаточное условие оптимальности в злп. Достаточное условие неразрешимости злп
- •8. Итерация симплекс–метода
- •11. Нахождение базиса угловой точки. Пример
- •12. Постановка тз. Построение нач. Плана перевозок методом северо-западного угла, методом мин. Элемента.
- •13. Определение закрытой модели тз. Критерий существования решения тз.
- •14. Исследование мн-ва клеток транспортной таблицы
- •15. Достаточное условие минимальности стоимости перевозок
- •16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •17. Метод исключения решения задачи на условный минимум. Пример.
- •18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
- •19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
- •20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
- •21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
- •22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
- •26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
- •27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
- •28.Определение двойственной задачи к задаче математического программирования.
- •29. Связь между двойственной и прямой задачами математического программирования.
- •30.Пример решения задачи оптимизации с помощью теории двойственности
- •31.Основные определения в задаче одномерной минимизации. Примеры.
- •33. Метод золотого сечения решения задачи одномерной минимизации.
- •34. Обоснование метода ломаных решения задачи одномерной минимизации.
- •35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
- •36.Алгоритм метода скорейшего спуска решения змм.
- •37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
- •38.Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
- •39.Сходимость метода скорейшего спуска.
- •41. Метод вариаций Лагранжа
- •42. Уравнение Эйлера
- •43. Случаи интегрируемости ур-ния Эйлера. Примеры.
- •44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
- •46. Задача вариационного исчисления с движущимся по кривой концом.
- •47. Примеры задач динамического программирования, их особенности
- •48.Принципы динамического программирования и функциональные уравнения Беллмана.
41. Метод вариаций Лагранжа
Пусть в задаче
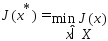 ,
где
,
где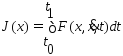
и

Пусть на кривой
 дости-тся
минимум, тогда все допустимые кривые
x(t),
из мн-ва X
можно представить в виде:
дости-тся
минимум, тогда все допустимые кривые
x(t),
из мн-ва X
можно представить в виде:
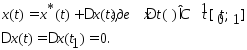
Тогда рассм. приращение функционала:
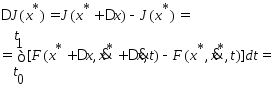
=/ в силу дифференцируемости ф-ции F/=
=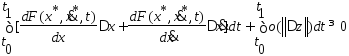
(т.к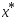 минимально),
где
минимально),
где бесконечно
малая велич.
бесконечно
малая велич.
Первый интеграл наз. 1-вой вариацией функционала.
В таком разложении
приращения функционала, кривые
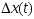 имеют произвольную природу, что влечет
за собой сложность исследования.
Представим кривые
имеют произвольную природу, что влечет
за собой сложность исследования.
Представим кривые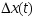 в виде однопараметрического семейства
ф-ций:
в виде однопараметрического семейства
ф-ций:
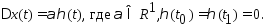
Для таких приращений функций рассмотрим приращение функционала:

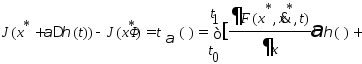
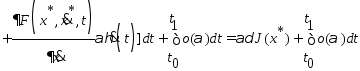
где

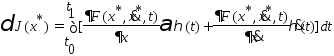
наз. первой вариацией функционала. Т.к
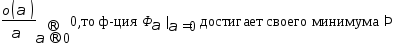
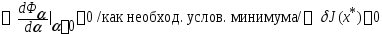
( на кривой подозрительной на минимум)
Замечание:Необходимое
условие оптимальности
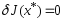 в силу произвольности ф-ций
в силу произвольности ф-ций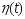 является неудобным для использования
на практике.
является неудобным для использования
на практике.
42. Уравнение Эйлера
Лемма
Дюбуа-Реймона.
Если
рав-во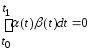 выполнено
для некоторой непрерывной ф-ии
выполнено
для некоторой непрерывной ф-ии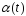 и
всех непрерывных ф-ий
и
всех непрерывных ф-ий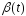 ,
уд.условию
,
уд.условию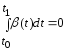 ,
то
,
то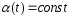 =с
на
=с
на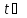
 .
.
Док-во.
Пусть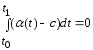 .
Для ф-ии
.
Для ф-ии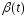 ,
кот.уд.условиям леммы, рассм.
,
кот.уд.условиям леммы, рассм.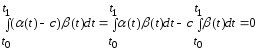 .(1).
Вместо
.(1).
Вместо
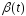 в (1) подставим
в (1) подставим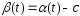 .
Тогда
.
Тогда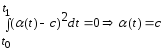 ,
т.к.
,
т.к.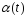 -непрерывная
ф-ия.
-непрерывная
ф-ия.
Следствие.Если
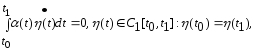
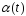 -непрерывная
ф-ия, то
-непрерывная
ф-ия, то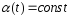 .
.
Теорема.
Пусть кривая
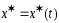 явл.
минималью в простейшей ЗВИ, то на ней
выполнено ДУ Эйлера
явл.
минималью в простейшей ЗВИ, то на ней
выполнено ДУ Эйлера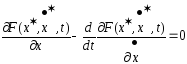 (2)
с краевыми условиями
(2)
с краевыми условиями
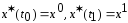 (3).
Док-во.
Пусть кривая
(3).
Док-во.
Пусть кривая
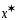 явл минималью ПЗВИ, то
явл минималью ПЗВИ, то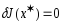 ,где
,где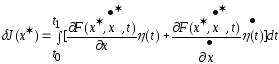 ,
,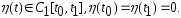 Рассмотрим
Рассмотрим
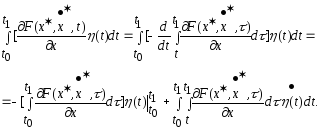
Тогда
 Используя
следствие к лемме получим
Используя
следствие к лемме получим
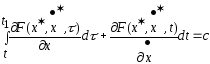 (4).
Ур-ние (4) наз. интегр.уравн.Эйлера,
(4).
Ур-ние (4) наз. интегр.уравн.Эйлера,
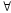 его
решение называется экстремалью. Перепишем
(4) так
его
решение называется экстремалью. Перепишем
(4) так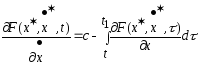 .
В правойчасти стоит ф-я диф. поt,
значит и в левой части стоит ф-я диф. по
t,
.
В правойчасти стоит ф-я диф. поt,
значит и в левой части стоит ф-я диф. по
t,
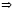
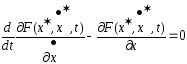
43. Случаи интегрируемости ур-ния Эйлера. Примеры.
1-й сл.
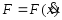 .
.
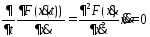 ,
,
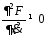 ,
т.к. задача явл. вырожденной, тогда
,
т.к. задача явл. вырожденной, тогда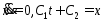
В задаче о кратчайшем расстоянии между 2мя точками плоскасти функционал имеет вид
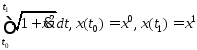
2й сл.
 .
.
В этом сл.ур-е Э-ра
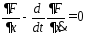 ,
,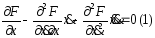 .
.
Для того, чтобы
найти
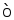 ур-я
(1) рассмотрим:
ур-я
(1) рассмотрим:
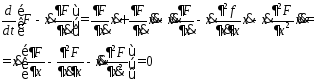
Если ф-я x(t)
явл решением ур-я (1), то
Отсюда получим,
что первый
 ур
Эйлера в этом случае имеет вид:
ур
Эйлера в этом случае имеет вид: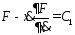 .
.
3й сл.
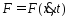 .
.
Тогда ур-е Эйлера
им. вид: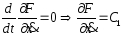
4й сл.
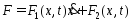 .
.
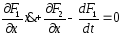 ,
,
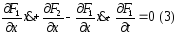
Если рав-во (3) не
явл тождеством, то оно определяет
некоторую линию x=x(t),
кот-я удовл-ет граничным условиям
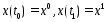 лишь
в исключит-ых случаях.
лишь
в исключит-ых случаях.
Если же ур-е (3) явл
тождеством, то подинтегральное выраж-е
представляет собой полный дифф-л
некоторой ф-и, тогда значение интеграла
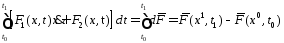
Значение интеграла не зависит от вида кривой, соединяющей граничные точки.
Пример. Исследовать на extr функционал

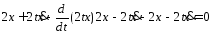
0=0 явл тождеством, значит ф-я подъинтегральная явл полным дифф-м, т.е.
 ,
,
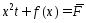 ,
,
тогда
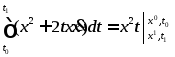
44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
Отрезок
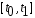 задан, значения
задан, значения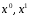 не закреплены, т.е. рассматривается
задача поиска минимума функционала
не закреплены, т.е. рассматривается
задача поиска минимума функционала
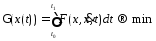 (1) где ф-ция
(1) где ф-ция
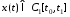 .
.
Теор1.
Пусть функция
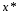 =
=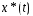 доставляет слабый локальный минимум
(1). Тогда эта ф-ция уд. ур-нию Эйлера.
доставляет слабый локальный минимум
(1). Тогда эта ф-ция уд. ур-нию Эйлера.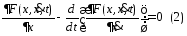
и краевым усл.
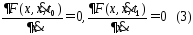
Док-во.
Рассм вариации Лагранжа
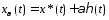 ,
где
,
где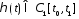 .
.
И необходимое усл.
минимума
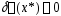 ,
где
,
где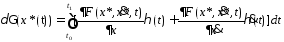 .
.
И образуем 1-ую вариацию функционала:
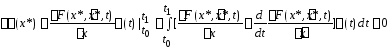
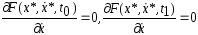 (2)
(2)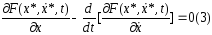
Т.о. доказали теор 1.
Замеч:
Если левый или правый конец траектории
закреплён, то первое или второе из
условий (2) заменяется
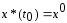 или
или .
.
45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
Рассм.
задачу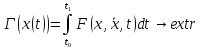 (1) где
(1) где
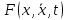 определена и непрерывна со всеми частными
производными до 2-ого порядка
включительно.Ищем
определена и непрерывна со всеми частными
производными до 2-ого порядка
включительно.Ищем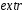 (1) при усл. когда отрезок [
(1) при усл. когда отрезок [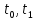 ]
не фиксирован. Значение ф-ии на концах
отрезка не заданы. Пусть
]
не фиксирован. Значение ф-ии на концах
отрезка не заданы. Пусть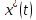 явл
решением рассм.задачи.Тогда найдётся
такие
явл
решением рассм.задачи.Тогда найдётся
такие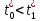 ,что
кривая
,что
кривая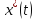 уд. уравн Эйлера и краевым усл.
уд. уравн Эйлера и краевым усл.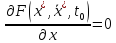 ,
,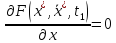 (2).
Определим усл. для значений
(2).
Определим усл. для значений
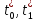 .
Рассм
.
Рассм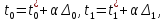 где
где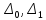 -
произвольные приращения интервала,
-
произвольные приращения интервала,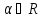 .
И предположим продолжимость решения
.
И предположим продолжимость решения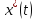 на отрезок [
на отрезок [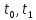 ],
если это необходимо. Рассмотрим
],
если это необходимо. Рассмотрим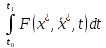 -
- (3)
(3)
В (4) рассм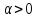 ,
разделим на
,
разделим на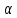 и
и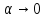 .
.
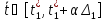 ,тогда
,тогда (4)
(4)
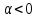 ,
,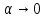 .
.
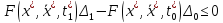 (5)
(5)
(4) должно выполняться
для
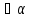 .
Значит (4) и (5) должны выполняться
одновременно. Значит:
.
Значит (4) и (5) должны выполняться
одновременно. Значит:
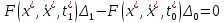 (6)
(6)
В (7)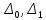 произвольны и независимы друг от друга,
поэтому
произвольны и независимы друг от друга,
поэтому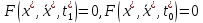 (7)
(7)
Т.о. справедлива теор 2.
Теорема 2.
Если
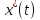 доставляет слабый минимум функционалу
(1) в задаче с незакреплёнными концами,
то кривая
доставляет слабый минимум функционалу
(1) в задаче с незакреплёнными концами,
то кривая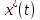 удовл ДУ Эйлера (2) и усл. (6) и (7).
удовл ДУ Эйлера (2) и усл. (6) и (7).
