
- •1.Понятие решения задачи мат. Программиров.
- •2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными задачи лп
- •6. Формула приращения целевой функции злп.
- •7. Достаточное условие оптимальности в злп. Достаточное условие неразрешимости злп
- •8. Итерация симплекс–метода
- •11. Нахождение базиса угловой точки. Пример
- •12. Постановка тз. Построение нач. Плана перевозок методом северо-западного угла, методом мин. Элемента.
- •13. Определение закрытой модели тз. Критерий существования решения тз.
- •14. Исследование мн-ва клеток транспортной таблицы
- •15. Достаточное условие минимальности стоимости перевозок
- •16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •17. Метод исключения решения задачи на условный минимум. Пример.
- •18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
- •19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
- •20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
- •21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
- •22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
- •26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
- •27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
- •28.Определение двойственной задачи к задаче математического программирования.
- •29. Связь между двойственной и прямой задачами математического программирования.
- •30.Пример решения задачи оптимизации с помощью теории двойственности
- •31.Основные определения в задаче одномерной минимизации. Примеры.
- •33. Метод золотого сечения решения задачи одномерной минимизации.
- •34. Обоснование метода ломаных решения задачи одномерной минимизации.
- •35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
- •36.Алгоритм метода скорейшего спуска решения змм.
- •37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
- •38.Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
- •39.Сходимость метода скорейшего спуска.
- •41. Метод вариаций Лагранжа
- •42. Уравнение Эйлера
- •43. Случаи интегрируемости ур-ния Эйлера. Примеры.
- •44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
- •46. Задача вариационного исчисления с движущимся по кривой концом.
- •47. Примеры задач динамического программирования, их особенности
- •48.Принципы динамического программирования и функциональные уравнения Беллмана.
16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
Под кл. методом подразум. подход к поиску точек экстремума ф-ций многих переменных, кот. основан на дифференц. исчислении.
Т1 Вейерштрасса(о
достижении верхней и нижней граней
непрер. ф-ции., опред-й на огранич.
замкнут.мн-ве). Пусть в задаче
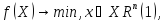 мн-во
мн-во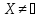 ,
ограничен-е, замкнутое, а ф-ция
,
ограничен-е, замкнутое, а ф-ция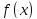 определена, конечна и непр-на наX.
Тогда
определена, конечна и непр-на наX.
Тогда
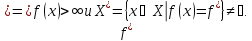
След.Пусть
X
- замкнуто,
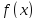 непреп. наX
и сущ. Точка
непреп. наX
и сущ. Точка
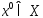
 ,такая,
что мн-во
,такая,
что мн-во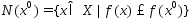
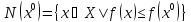 ограничено.Тогда
ограничено.Тогда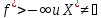 .
.
Т-ма2.Пусть
ф-ция
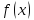 диф-ма в точке
диф-ма в точке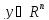 .
Еслиy
есть точка лок-го минимума ф-ции
.
Еслиy
есть точка лок-го минимума ф-ции
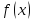 ,то
выполн. усл.стационарности
,то
выполн. усл.стационарности
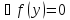 .Д-во. Возьмем
произв. точку
.Д-во. Возьмем
произв. точку
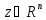 и построим
приращение аргумента
и построим
приращение аргумента
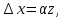 где
где
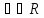 .
Рассм. Приращ. ф-ции в точкеy,
которое разложим на основании
опред.диф.ф-ции
.
Рассм. Приращ. ф-ции в точкеy,
которое разложим на основании
опред.диф.ф-ции
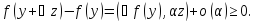 Разделим последнее равенство на
Разделим последнее равенство на
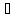 и устремим
и устремим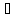 к нулю. В пределе получим нерав-во
к нулю. В пределе получим нерав-во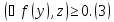 В соотн.(3) положим
В соотн.(3) положим
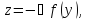 из чего получим нерав-во
из чего получим нерав-во
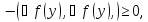 котрое может выпол. Только при усл.
котрое может выпол. Только при усл.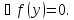
Зам1.Точки
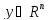 ,
для кот. выпол. Рав-во
,
для кот. выпол. Рав-во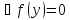 ,
наз. стационарными. Поиск точек минимума
можно начинать с реш-я системы n
ур-ний с n
неизв-ми величинами
,
наз. стационарными. Поиск точек минимума
можно начинать с реш-я системы n
ур-ний с n
неизв-ми величинами
 Зам2.Не
всякая стац. точка явл. точкой лок. экстр.
Пример1.Исслед.
на экстр. ф-ю двух переменных
Зам2.Не
всякая стац. точка явл. точкой лок. экстр.
Пример1.Исслед.
на экстр. ф-ю двух переменных
 .Р-е.Выч.
градиент данной ф-и
.Р-е.Выч.
градиент данной ф-и
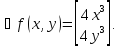 Из
усл. стац. получаем одну точку (0,0),
подозрит. на экстр. Знач. ф-и в стац. т-ке
равно нулю:
Из
усл. стац. получаем одну точку (0,0),
подозрит. на экстр. Знач. ф-и в стац. т-ке
равно нулю: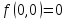 .Но
.Но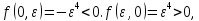 из чего след., что т-ка (0,0) эктр. не
явл.Т-ма3.Пусть
ф-ция
из чего след., что т-ка (0,0) эктр. не
явл.Т-ма3.Пусть
ф-ция
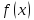 дважды диф-ма в точке
дважды диф-ма в точке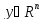 .
Если у есть точка лок. миним. зад. (1),то
матрица
.
Если у есть точка лок. миним. зад. (1),то
матрица ,
составленная их вторых частных производ.
ф-ии f
в точке y,
неотриц. Определена,т.е. для всех
,
составленная их вторых частных производ.
ф-ии f
в точке y,
неотриц. Определена,т.е. для всех
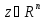 вып. нер-во
вып. нер-во
 Д-во
Рассм. Приращение цел. ф-ии в т. y
соотв-щее приращ. аргум.
Д-во
Рассм. Приращение цел. ф-ии в т. y
соотв-щее приращ. аргум.
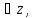 где
где
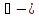 малое,
малое,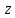 -
произв. в-ор
-
произв. в-ор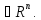 Т.к. ф-яf
дважды диф., тосправедливо
Т.к. ф-яf
дважды диф., тосправедливо
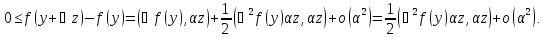
Т4 (достат.усл.оптим-ти).
Пусть в з.(1)
ф-я f(x)
дважды диф-ма. Т-ка
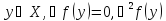 строго
полож.опред-на,т.е.
строго
полож.опред-на,т.е.
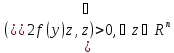 .Тогдаy
есть решение з.(1)
Док-во. Пусть
в т. у вып-ны усл-я т-мы, но т. y
не явл. Реш. з.Это означает, что сущ.
Посл-ть точек
.Тогдаy
есть решение з.(1)
Док-во. Пусть
в т. у вып-ны усл-я т-мы, но т. y
не явл. Реш. з.Это означает, что сущ.
Посл-ть точек
 Представим
Представим
 ,
,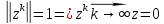 .
Рассм.
.
Рассм.
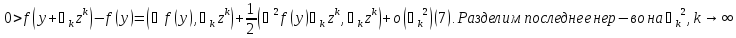 и учтем
и учтем
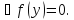 Получим
Получим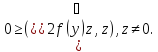 Получим противоречие, кот. док-ет
т-му.Пример.Исслед.
на экстр. ф-ю
Получим противоречие, кот. док-ет
т-му.Пример.Исслед.
на экстр. ф-ю
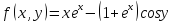 .
.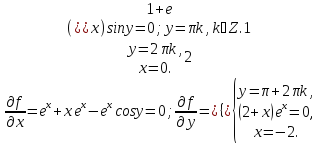 Строим
матрицу 2-х произв.
Строим
матрицу 2-х произв.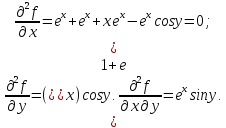 Подст.
Подст. по крит.Сильвестра полож.опред. Т.
по крит.Сильвестра полож.опред. Т.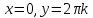 т-ки минимума.
т-ки минимума.
 .
.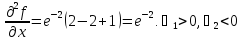 .Квадр.ф-я
не явл. знакоопред. поэтому не вып-но
необход.усл.2-го порядка и в т-х
.Квадр.ф-я
не явл. знакоопред. поэтому не вып-но
необход.усл.2-го порядка и в т-х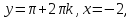 нет
экстр.В т-ме3 и т-ме4 при исслед.з. наmax
знакоопред-ть квадр-й формы следует
поменять на противоположную.
нет
экстр.В т-ме3 и т-ме4 при исслед.з. наmax
знакоопред-ть квадр-й формы следует
поменять на противоположную.
17. Метод исключения решения задачи на условный минимум. Пример.
Рассм.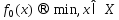 (1)
(1)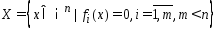 (2).
(2).
Предпол-ся, что
ф-ции
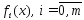 определены
и имеют производные 1-го порядка на всем
пр-ве
определены
и имеют производные 1-го порядка на всем
пр-ве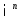 .
.
Если систему
ограничений (2) можно представить в виде
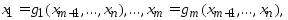 ,
то зад. (1),(2) свод-ся к зад. безусловной
минимизации.
,
то зад. (1),(2) свод-ся к зад. безусловной
минимизации.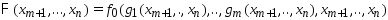 .
.
Теорет-я возможность применения такого метода исключ.основывается на т-ие о неявных ф-ях.
Т1 о неявных
ф-циях. Пусть
рассм. m-мерная
ф-ция
 .Изв.т.
.Изв.т.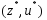 ,для
кот.
,для
кот.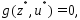
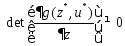 ,тогда
сущ.m-мерная
ф-я
,тогда
сущ.m-мерная
ф-я
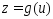 ,
уд.усл.:1)
,
уд.усл.:1)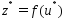 ;2)
;2)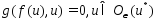 ;3.
;3. имеет
в
имеет
в
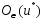 непрер-е производные того же порядка,
что и ф-ция
непрер-е производные того же порядка,
что и ф-ция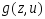 по
по .
.
Т2.
Метод искл.реш-я в з. (1),(2)применим, если
в окрестности точки минимума
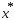 ф-ции
ф-ции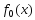 ф-ции
ф-ции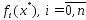 диф-мы и
диф-мы и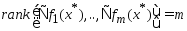 .
.
Д-во: Из
усл.(3)=>что у м-цы
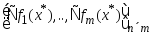 сущ.хотя
бы 1 ненулевой минор порядкаm.Предпол-м,
что минор распол-ся в первых m
строках этой матрицы.В противном случае
переобозн. переменные.В принятом
предпол-и обозн. Первые m
компонент в-ра x
через z,
а ост-е n-m
компонент через в-ор u.Набор
ф-ий
сущ.хотя
бы 1 ненулевой минор порядкаm.Предпол-м,
что минор распол-ся в первых m
строках этой матрицы.В противном случае
переобозн. переменные.В принятом
предпол-и обозн. Первые m
компонент в-ра x
через z,
а ост-е n-m
компонент через в-ор u.Набор
ф-ий
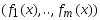 тогда
обозн. ч/з
тогда
обозн. ч/з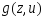 .
Тогда система огран-ий
.
Тогда система огран-ий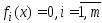 примет
вид
примет
вид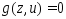 и для этой ф-ии в т.
и для этой ф-ии в т.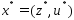 вып-ны
все усл. т-мы1.
вып-ны
все усл. т-мы1.
Замечание.
Возможность прим-ия метода искл. сущ-но
огранич-ся сложностью решения с-мы
урав-ий
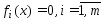 в явном виде.
в явном виде.
Пример1.Исслед.
на экстр. ф-ю
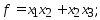
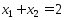 .
.
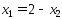 ;
;
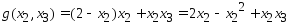 ;
;
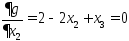 ;
;
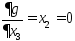

(0;-2)-стац точка.
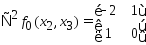
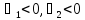 -знакопеременна(не
вып.необход.усл. 2-го порядка).Т.(0,-2) не
явл.экстр-й для ф-ии g..Исх.ф-я
экстремума не имеет.
-знакопеременна(не
вып.необход.усл. 2-го порядка).Т.(0,-2) не
явл.экстр-й для ф-ии g..Исх.ф-я
экстремума не имеет.
