
- •1.Понятие решения задачи мат. Программиров.
- •2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными задачи лп
- •6. Формула приращения целевой функции злп.
- •7. Достаточное условие оптимальности в злп. Достаточное условие неразрешимости злп
- •8. Итерация симплекс–метода
- •11. Нахождение базиса угловой точки. Пример
- •12. Постановка тз. Построение нач. Плана перевозок методом северо-западного угла, методом мин. Элемента.
- •13. Определение закрытой модели тз. Критерий существования решения тз.
- •14. Исследование мн-ва клеток транспортной таблицы
- •15. Достаточное условие минимальности стоимости перевозок
- •16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •17. Метод исключения решения задачи на условный минимум. Пример.
- •18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
- •19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
- •20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
- •21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
- •22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
- •26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
- •27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
- •28.Определение двойственной задачи к задаче математического программирования.
- •29. Связь между двойственной и прямой задачами математического программирования.
- •30.Пример решения задачи оптимизации с помощью теории двойственности
- •31.Основные определения в задаче одномерной минимизации. Примеры.
- •33. Метод золотого сечения решения задачи одномерной минимизации.
- •34. Обоснование метода ломаных решения задачи одномерной минимизации.
- •35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
- •36.Алгоритм метода скорейшего спуска решения змм.
- •37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
- •38.Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
- •39.Сходимость метода скорейшего спуска.
- •41. Метод вариаций Лагранжа
- •42. Уравнение Эйлера
- •43. Случаи интегрируемости ур-ния Эйлера. Примеры.
- •44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
- •46. Задача вариационного исчисления с движущимся по кривой концом.
- •47. Примеры задач динамического программирования, их особенности
- •48.Принципы динамического программирования и функциональные уравнения Беллмана.
35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
Выбирем некот т-ку
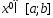 .
Построим ф-ю
.
Построим ф-ю
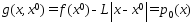 и определим
и определим
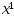 из усл.
из усл.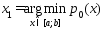 .
Очевидно, чтоx1=a
или x1=b.
Пусть в результате выполнения нескольких
шагов определены т-ки х1,х2,…,хn,
n
.
Очевидно, чтоx1=a
или x1=b.
Пусть в результате выполнения нескольких
шагов определены т-ки х1,х2,…,хn,
n .
Построим ф-цию g(x,xn)=f(xn)-L|x-
xn
|.
.
Построим ф-цию g(x,xn)=f(xn)-L|x-
xn
|.
Строим ф-цию
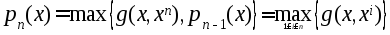 Следующее
приближение
Следующее
приближение
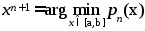
Процесс вычисл.
продолж. до тех пор, пока не будет
выполнено нерав-во
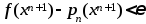 ,
где
,
где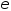 - заданная точность. В кач-ве решения
задачи выбирается т-ка
- заданная точность. В кач-ве решения
задачи выбирается т-ка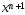 .
.
Зам.Метод ломаных сходится при любом начальном при любом начальном приближении.
Зам.
Для всех х справедливо соотнош.
справедливо соотнош.
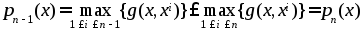
т.е. ф-ции рn(х) приближают ф-цию f(x) снизу, оставаясь каждый раз не выше графика ф-ции f(x).
Зам, Недостаток – с ростом числа шагов растет требуемый объем памяти вычисл машины.
Зам. Для применения метода надо знать константу Липшица.
Теорема.
Пусть ф-я
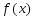 уд. усл. Липшица на [a;b],
тогда посл-ть
уд. усл. Липшица на [a;b],
тогда посл-ть
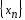 полученная
методом ломанных такая, что:
полученная
методом ломанных такая, что:
1)
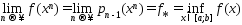 (1),
причем
(1),
причем
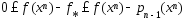 (2)
(2)
2)
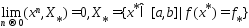 (3)
(3)
Док-во.
Рассмотрим
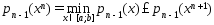 (4)
(4)
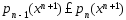 (5),
(5),
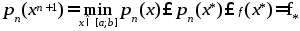 (6)
, где
(6)
, где
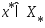 .
Из (4)-(6) получаем
.
Из (4)-(6) получаем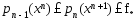
т.е. послед-ность
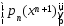 явл. возрастающей и ограничена сверху,
поэтому
явл. возрастающей и ограничена сверху,
поэтому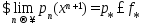 .
Кроме того, из (4)-(6) следует оценка (2).
Покажем, что
.
Кроме того, из (4)-(6) следует оценка (2).
Покажем, что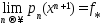 .
Т.к.
.
Т.к.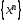 ограничена,
то из нее можно выделить сходящуюся
подпослед-ность
ограничена,
то из нее можно выделить сходящуюся
подпослед-ность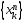 .
Пусть
.
Пусть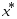 - некотор.
т-ка послед-ности
- некотор.
т-ка послед-ности
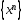 .
Послед-ность
.
Послед-ность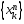 сходится к т-ке
сходится к т-ке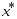 при
при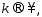 n1<n2<…<nk<…
n1<n2<…<nk<…
Пример. f(x)=|x2-1|,
x
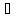 [-2,3].
На отр. [-2,3] ф-ция уд. усл. Липшица с
константойL1=4,
на отр. [-1,1] L2=2,
на отр. [1,2] L3=6.
На всем отр. L=6.
Строим ф-цию g(x,0)=1-6|x|.
При x<0,
g(x,0)=1+6x,
g(-1,0)=-5,
x>0,
g(x,0)=1-6x,
g(1,0)=-5.
Т-ка x1.
g(x,3)=8-6|x-3|,
g(x,3)=8+6x-18.
[-2,3].
На отр. [-2,3] ф-ция уд. усл. Липшица с
константойL1=4,
на отр. [-1,1] L2=2,
на отр. [1,2] L3=6.
На всем отр. L=6.
Строим ф-цию g(x,0)=1-6|x|.
При x<0,
g(x,0)=1+6x,
g(-1,0)=-5,
x>0,
g(x,0)=1-6x,
g(1,0)=-5.
Т-ка x1.
g(x,3)=8-6|x-3|,
g(x,3)=8+6x-18.
Следующ. т-ка x2 определ. как min g(x,-2)=3-6|x+2|, g(x,-2)=3-6x-12
36.Алгоритм метода скорейшего спуска решения змм.
Пусть выбрано
некот нач-е приближение
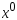 и на некоторой итерации построено
очередное приближение
и на некоторой итерации построено
очередное приближение и
вычислены значения
и
вычислены значения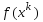 ,
,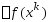 .
Рассм.луч, проходящий ч/з т
.
Рассм.луч, проходящий ч/з т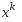 в
направлении антиградиента
в
направлении антиградиента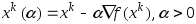 .В
этом луче рассм. ф-ю, зависящую от альфа
.В
этом луче рассм. ф-ю, зависящую от альфа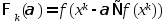 .
Рассм. вспомогательную задачу одномерной
минимизации
.
Рассм. вспомогательную задачу одномерной
минимизации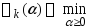 (*).
(*).
И пусть решение
этой задачи достигается в т
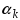 :
: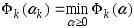 ,
тогда след. приближение вычисляется по
ф-ле
,
тогда след. приближение вычисляется по
ф-ле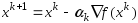 .
.
Итерационный процесс продолжается до тех пор, пока не будет выполнен критерий окончания счета.
В качестве критерия окончания счета могут использоваться нерав-ва:
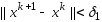 ;
;
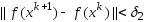 ;
;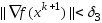 ,где
,где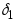 ,
,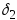 ,
,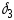 –заданные
числа, характеризующие точность счета
–заданные
числа, характеризующие точность счета
Если на некоторой
итерации выполняется рав-во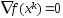 ,
то в т-ке хk
выполн. необход. усл. Оптимальности и
итерационный процесс заканчивается.
,
то в т-ке хk
выполн. необход. усл. Оптимальности и
итерационный процесс заканчивается.
Если
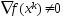 ,
то сущ.такое неотрицат.
,
то сущ.такое неотрицат.
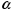 ,
что
,
что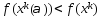 .
.
Если значения
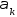 явл. решением задачи (*), то в этой т-ке
должно быть выполнено необходимое усл.
оптимальности, т.е.
явл. решением задачи (*), то в этой т-ке
должно быть выполнено необходимое усл.
оптимальности, т.е.
Вычислим эту
производную в т-ке
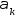
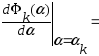

Получаем, что градиенты, вычисл. в соседних приближениях, постоенных методом скорейшего спуска ортогональны.
Зам.
Величину
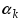 можно выбирать из условия
можно выбирать из условия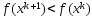 ,
в этом случае метод наз градиентным.
,
в этом случае метод наз градиентным.
37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
1)алгоритм
метода условного градиента. Пусть
задано начальное приближение
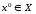 и методом условного градиента вычислено
и методом условного градиента вычислено Строим ф-цию
Строим ф-цию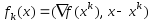 и решаем задачу
и решаем задачу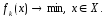 (1)
(1)
Пусть

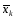 есть решение задачи. Заметим, что
есть решение задачи. Заметим, что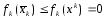 .
Если
.
Если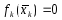 ,
то
,
то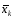 уд.
необходимому усл. и вычислительный
процесс заканчивается. Если
уд.
необходимому усл. и вычислительный
процесс заканчивается. Если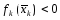 ,
то строим отрезок
,
то строим отрезок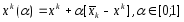 (2)
на этом отрезке рассматриваем ф-цию
(2)
на этом отрезке рассматриваем ф-цию
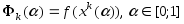 и
решаем задачу
и
решаем задачу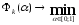 (3).
(3).
Тогда
след.приближение находится по формуле
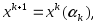 где
где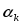 есть
решение задачи (3).
есть
решение задачи (3).
Практическим
критерием окончания счета выбираются
нер-ва
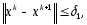
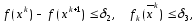 где
где
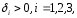 согласованные числа, характеризующие
точность счета.
согласованные числа, характеризующие
точность счета.
Замеч1. Метод условного градиента эффективен когда вспомогат. задача (1) допускает простое решение.
Замеч2.Часто
на практике задают некоторое значение
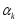 ,
н/р,
равное 1, проверяют усл.
,
н/р,
равное 1, проверяют усл.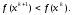 .
Если
оно не выполняется, то
.
Если
оно не выполняется, то
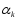 уменьшают,
например, в два раза и т.д.
уменьшают,
например, в два раза и т.д.
2)алгоритм
метода проекции градиента.
Пусть задано нач. приближение
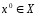 и
методом проекции градиента вычислено
и
методом проекции градиента вычислено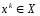 .
След.приближение ищется по формуле
.
След.приближение ищется по формуле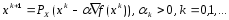 (4)
В зависимости от выбора
(4)
В зависимости от выбора
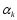 строятся различные варианты метода
проекции градиента. Например,
строятся различные варианты метода
проекции градиента. Например,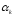 может находиться как решение задачи
одномерной минимизации
может находиться как решение задачи
одномерной минимизации
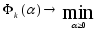 (5),
где
(5),
где
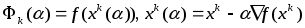 (6)
(6)
В
этом случае при
 метод проекции градиента превращается
в метод скорейшего спуска.
метод проекции градиента превращается
в метод скорейшего спуска.
Часто
при практическом исп. метода (4) находят
такое
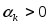 ,
что выполняется условие релаксационности
,
что выполняется условие релаксационности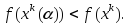
При
его нарушении полагают
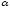 равным
равным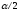 снова проверяют условие релаксационности
и т. д.
снова проверяют условие релаксационности
и т. д.
В
качестве критерия окончания счета
выбираются неравенства
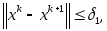
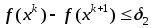 ,
где
,
где —
числа, характеризующие точность счета.
—
числа, характеризующие точность счета.
Замеч4. Главная сложность реализации метода проекции градиента заключается в решении задачи проектирования.
