30.Метод ломаных. Обоснование и алгоритм. Пример.
Метод ломаных применяется для решения задачи (1), без требования унимодальности функции f.
Опр.
Говорят, что ф
удовлетворяет условию Липшица на [a;b],
если
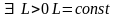, такая что
.
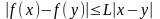
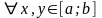(2) Условие Липшица означает, что угловые
коэффициенты хорд, кот соединяют точки
(x,f(x))
и (y,f(y))
не превосходит константы L.
я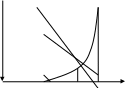
Рис1
Если ф-я удовлетворяет условию Липшица на [a;b] то она явл-ся непрерывной на [a;b].
Пусть
ф-я f(x)
удовлетворяет на [a;b]
условию Липш (2) с константой L.
Зафиксируем некоторую точку y
из [a;b]
и рассмотрим ф-ю
,
(см рис 1). Ф-я g
представляет собой кусочно-гладкую
ф-ю, ее график есть ломаная с углами
наклона l
и –l,
проходящая ч/з точку (y,f(y)).
Рассмотрим
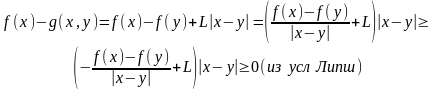т.е.
,
.
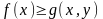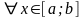Описание м. ломанных
Выбирем
некот т
.
Построим ф-ю
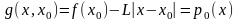и
определим
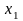из условия
,
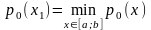очевидно что x1=a
или x1=b.
Далее строим ф-ю
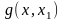и
и т
:
.
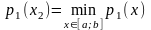Пусть на некот шаге известны х1,х2,…,х(n-1),
строим ф-ю
=
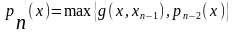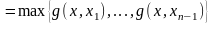и т
:
.
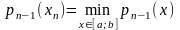Если минимум достигается в нескольких
точках, то берут любую.
Зам.
Ф-я
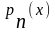представляет собой кусочно-гладкую
ф-ю, ее график есть ломаная с углами
наклона l
и –l.
Зам.
Ф-я
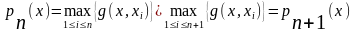
Зам.
.
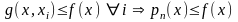Т. Обр, задача минимизации ф-ции f
заменяется задачей минимизации ф-ции
p,
кот приближает f
снизу. Причем, р монотонно возрастает.
Докажем сходимость м ломанных.
Т.
Пусть ф-я
удовлетворяет условию Липшица на [a;b],
тогда посл-ть
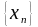полученная м ломанных такая, что:
1)
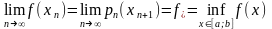, причем
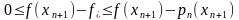(3)
2)
последовательность
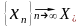Док-во.
Рассм. произвольную точку
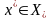и построим посл-ть соотношений
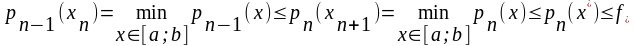(4)
След-но,
посл-ть
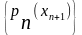монотонно возрастает и ограничена
сверху, поэтому
.
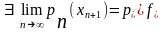Кроме того, из (4)=>(3). Покажем, что
.
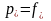Тк
ограничена, то из нее можно выделить
сходящуюся подпоследовательность, нпр
.
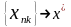Пусть
-
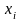некотор т, построенная м ломаных, тогда
,
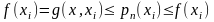получаем, что
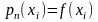Рассмотрим
=
=
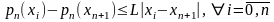(5). Возьмем в качестве
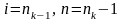и подставим их в (5):
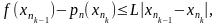тк посл-ть
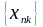содержиться, то
.
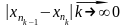Тогда
=>
.
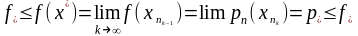Тк точка
была выбрана произвольно, то =>
справедливость 1) данной теоремы. А 2)=>
ет из Т.Вейерштрассе. Конец док-ва.
Зам.
Из теоремы => что процесс вычисления
заканчивается в случаи выполнения
нер-ва
Зам. М ломаных сходится при любых начальных приближениях.
Зам, Недостаток – с ростом числа шагов растет требуемый объем памяти вычисл машины.
Зам. Для применения метода надо знать константу Липшица.
31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
Описание м. ломанных
Выбирем некот т . Построим ф-ю
и определим из условия , очевидно что x1=a или x1=b. Далее строим ф-ю и и т : . Пусть на некот шаге известны х1,х2,…,х(n-1), строим ф-ю = и т : . Если минимум достигается в нескольких точках, то берут любую.
Зам. Ф-я представляет собой кусочно-гладкую ф-ю, ее график есть ломаная с углами наклона l и –l.
Зам. Ф-я
Зам. . Т. Обр, задача минимизации ф-ции f заменяется задачей минимизации ф-ции p, кот приближает f снизу. Причем, р монотонно возрастает.
Докажем сходимость м ломанных.
Теорема. Пусть ф-я удовлетворяет условию Липшица на [a;b], тогда посл-ть полученная м ломанных такая, что:
1) , причем (3)
2) последовательность
Док-во. Рассмотрим произвольную точку и построим посл-ть соотношений (4)
След-но, посл-ть монотонно возрастает и ограничена сверху, поэтому . Кроме того, из (4)=>(3). Покажем, что . Тк ограничена, то из нее можно выделить сходящуюся подпоследовательность, нпр . Пусть - некотор т, построенная м ломаных, тогда
, получаем, что Рассмотрим = = (5). Возьмем в качестве и подставим их в (5): тк посл-ть содержиться, то . Тогда => . Тк точка была выбрана произвольно, то => справедливость 1) данной теоремы. А 2)=> ет из Т.Вейерштрассе. Конец док-ва.
Зам. Из теоремы => что процесс вычисления заканчивается в случаи выполнения нер-ва
Зам. М ломаных сходится при любых начальных приближениях.
Зам, Недостаток – с ростом числа шагов растет требуемый объем памяти вычисл машины.
Зам. Для применения метода надо знать константу Липшица.
32.
Обоснование и алгор.метода скорейшего
спуска.
Рассм. задачу
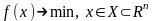(1). Ф-я f(x)
предполагается определенной, принимающей
конечные знач. и непрерывно диффер-ой.
Необх. усл. для з (1) имеют вид: Q(x*)=0,
где
.
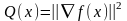Мн-во
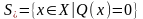наз
мн-вом стационарных точек з (1). Мн-во
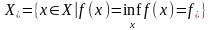решений
з (1). Очевидно, что
.
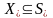Если Q(x)<>0,
то направление найскорейшего возраст.
ф-и f(x)
в т х совпадает с направлением град. в
этой точке, а направление наискор-го
убыв. – с направлением антиград.. Это
св-во лежит в основе градиентных методов.
Эти методы предполагают выбор некот.нач-го
приближения, однако общих правил выбора
этого значения нет. Опр.
Посл-ть,
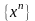построенная
с помощью некот итерационного процесса
наз релаксационной, если
.
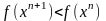Итерационный процесс тогда наз
релаксационным. Нер-во Q(x)>0
обеспечивает релаксационность процесса,
поэтому если доказать, что
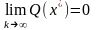(2), то можно говорить, что такой процесс
характеризует стремление к выполнению
необходимого условия минимума. Но не
всякий релаксационный процесс со св-вом
(2) генерирует посл-ть точек сходящихся
к
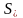.Алгоритм
метода скорейшего спуска.
Пусть выбрано некот нач-е приближение
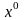и на некоторой итерации вычислено
значение
,
,
.
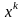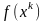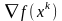Рассмотрим луч, проходящий ч/з т
в
направлении антиградиента
.
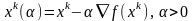В этом случае рассмотрим ф-ю, зависящую
от альфа
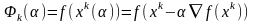.Рассмотрим
вспомогательную задачу одномерной
минимизации
.
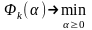И пусть решение этой задачи достигается
в т
:
,
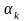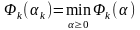тогда следующее приближение вычисляется
по ф-ле
.
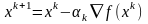Если в некот точке
,
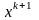
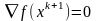то эта точка будет подозрительной на
минимум и процесс вычислений заканчивается.
Геом.интерпритация метода: Ф-я
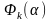достигает своего миним. в
точке
.
Вычислим
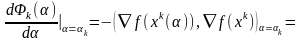
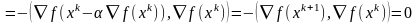
Получаем,
что градиенты ЦФ в соседних точках
вычисленные по МНС-ортогональны.Зам.
Величину
можно выбирать из усл.
,
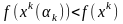в этом случае метод наз Градиентным.Зам.
Закончить процесс вычисления в град.
методе можно при усл., что
,
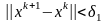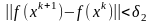и
,
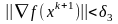где
,
,
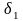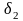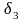– согласованные числа.
Т.Пусть
ф-я f(x)
явл непрер. диффер-ой, огран.снизу и ее
град. удовлетв. векторному усл.Липшица
на всем пр-ве
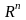(т.е.
).
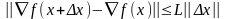Тогда для любого нач-го приближения
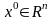итерац. процесс метода наискор. спуска
является релаксационным и удовлетв.
усл.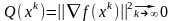
.
Если дополнительно предположить, что
мн-во
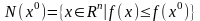– ограничено , то посл-ть
,
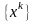построенная МНС, сх-ся к непустому мн-ву
стац-х точек
.
Если кроме этого ф-я f(x)
явл выпуклой, то посл-ть
явл-ся минимизирующей, сходящейся к
непустому мн-ву реш. задачи
