
- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
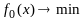 (1)
(1)
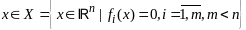 (2)
(2)
Опр.
Задача (1),(2) наз нормальной в точке
,
если среди обобщенных векторов Л.,
ссответств точке
нет таких, что
 ;
вектор
в таком случае наз норм-ным.
;
вектор
в таком случае наз норм-ным.
Опр.
Вектор
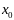 наз обыкн планом, если вектора (3)
наз обыкн планом, если вектора (3)
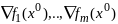 лин независимы. Зам1.
Условие (3) наз усл Люстерника. Т1
Оптим план
явл нормальнам тогда и только тогла,
когда он обыкновенный.
лин независимы. Зам1.
Условие (3) наз усл Люстерника. Т1
Оптим план
явл нормальнам тогда и только тогла,
когда он обыкновенный.
Док-во:
Необх.
Пусть
-оптим
норм план, и.е. сущ такие множит
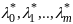 ,
что
,
что
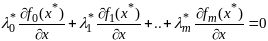 (4).
Причем, т.к.
–норм
план, то
(4).
Причем, т.к.
–норм
план, то
 .
Предположим, что при этом план
не явл обыкновенным, т.е. вектора
.
Предположим, что при этом план
не явл обыкновенным, т.е. вектора
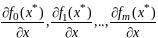 (5)
явл лин зависим
найдутся числа
(5)
явл лин зависим
найдутся числа
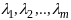 одновременно
,
обращающие в 0 лин комбинацию векторов
(5). Тогда в рав-ве (4) при найденных знач
получим, что
одновременно
,
обращающие в 0 лин комбинацию векторов
(5). Тогда в рав-ве (4) при найденных знач
получим, что
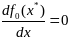 .
Тогда можно взять и
.
Тогда можно взять и
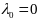 ,
что противоречит норм-ти плана
.
,
что противоречит норм-ти плана
.
Достат.
Пусть
явл оптим обыкнов
вектора
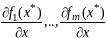 (*)
явл лин независ. По Т об обобщ прав мн
Л. сущ числа
,
одновременно
,
что
(*)
явл лин независ. По Т об обобщ прав мн
Л. сущ числа
,
одновременно
,
что
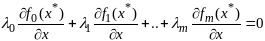 .Предположим, что план
не явл норм,
,
тогда получаем, что среди чисел
есть
,
что означаем лин зависимость векторов
(*).?!.
Т2 (классич
правило мн Л).
Ф-ция Л.
.Предположим, что план
не явл норм,
,
тогда получаем, что среди чисел
есть
,
что означаем лин зависимость векторов
(*).?!.
Т2 (классич
правило мн Л).
Ф-ция Л.
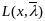 при
при
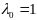 наз классич ф-цией Л, и обознач
наз классич ф-цией Л, и обознач
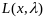 :
:
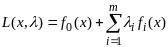 .
Пусть на оптим плане
задачи (1),(2) вектора (*) лин независ, тогда
сущ и единственны числа
.
Пусть на оптим плане
задачи (1),(2) вектора (*) лин независ, тогда
сущ и единственны числа
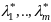 ,
такие что
,
такие что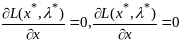 (6).
(6).
Док-во.
В усл Т2 вектор
явл норм, т.е. в условиях обобщенного
правила мн Л можно считать
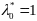 .
Тогда 1-ое из условий (6) предст собой
условие обобщенного правила мн Л, а 2-ое
– систему ограничений исходной задачи.
.
Тогда 1-ое из условий (6) предст собой
условие обобщенного правила мн Л, а 2-ое
– систему ограничений исходной задачи.
Пусть
в задаче (1),(2) ф-ции
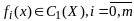 Опр.Вектор
Опр.Вектор
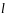 наз направлением допустимым в точке
по огранич
наз направлением допустимым в точке
по огранич
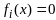 ,
если
,
если
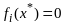 и скал произведение
и скал произведение
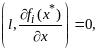 .
Допустим направл явл касательным
направлением по соответств ограничению.
Опр.
Вектор
наз допустимым направл по ограничениям
задачи (1),(2) в точке
,
если этот вектор явл допустимым
направлением по каждому ограничению
задачи (1),(2). Опр.
Вектор
наз подходящим направл ф-ции
.
Допустим направл явл касательным
направлением по соответств ограничению.
Опр.
Вектор
наз допустимым направл по ограничениям
задачи (1),(2) в точке
,
если этот вектор явл допустимым
направлением по каждому ограничению
задачи (1),(2). Опр.
Вектор
наз подходящим направл ф-ции
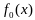 в точке
,
если скал произв
в точке
,
если скал произв
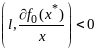 .Подходящ напр ф-ции явл направлением
её убывания. Опр.
Вектор
наз подходящим напр задачи (1),(2) в точке
,
если этот вектор явл допустимым по всем
ограничениям задачи и явл подходящим
напр её целевой ф-ции. Т1.
Если
явл оптим, обыкнов. планом задачи (1),(2),
то в точке
не сущ подходящих направлений
задачи(1),(2), т.е. для всех векторов
,
удовл условию
.Подходящ напр ф-ции явл направлением
её убывания. Опр.
Вектор
наз подходящим напр задачи (1),(2) в точке
,
если этот вектор явл допустимым по всем
ограничениям задачи и явл подходящим
напр её целевой ф-ции. Т1.
Если
явл оптим, обыкнов. планом задачи (1),(2),
то в точке
не сущ подходящих направлений
задачи(1),(2), т.е. для всех векторов
,
удовл условию
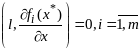 (7),
(7),

Зам.
Если решается задача на максимум и точка
явл оптим, обыкнов планом , то для всех
векторов удовлетворяющих (7) вып нер-во
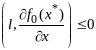 .
.
Зам.
Т1 предст собой необх усл 1-го порядка.
Т2 Пусть
в задаче (1),(2) ф-ции
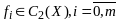 .
Если
явл оптим, обыкнов планом задачи (1),(2),
а
.
Если
явл оптим, обыкнов планом задачи (1),(2),
а
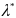 -
соответств ему вектор мн Л, то квадратичная
-
соответств ему вектор мн Л, то квадратичная
форма
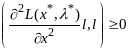 для всех векторов
,
удовл усл (7).
для всех векторов
,
удовл усл (7).
Зам.
Если решается задача на максимум, то
квадрат форма втор производных ф-ции Л
 ,
т.е.
,
т.е.
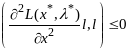 для всех векторов удовлетв (7).
для всех векторов удовлетв (7).
