
- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
27. Основные определения в задаче одномерной минимизации. Примеры.
f(x)→min,

Предп.,
что f(x)
принимает
на X
конечные значения.
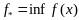 ,
,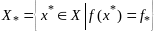
Опр. Посл-ть {xk} из X наз. минимизирующей для функции f(x) на мн-ве Х, если
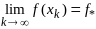 .
.
Замеч. Из опр-ния и существования точной нижней грани следует, что min-щая посл-ть всегда.
Опр.
Посл-ть {xk}
сходится к Х,
если
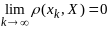 .
.
Замеч. Если мн-во Х* не явл. пустым, то всегда min-щая посл-ть, сходящаяся к Х*.
Пример . Множ-во решений задачи min-ции f(X)
Х*={0},
f*
=0. Посл-ть
xk=k
явл. минимизир. для f(x):
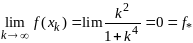

Опр.
Функция f(x)
наз.
унимодальной на [a;b],
если она непр. на этом отрезке и
 такие
числа α,
β,
a≤α≤
β≤b,
что ф-ция f(x)
строго монотонно убывает при a≤x≤α,
если a<α;
такие
числа α,
β,
a≤α≤
β≤b,
что ф-ция f(x)
строго монотонно убывает при a≤x≤α,
если a<α;
строго монотонно возрастает при β≤x≤b, если β<b. f(x)=f* при α≤x≤β
Случаи,
когда один или два из отрезков
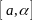 ,
,
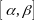 ,
,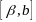 вырожд.
в точку не исключ.
вырожд.
в точку не исключ.
Если α=β, функция наз. строго унимодальной.
28.Метод деления отрезка пополам решения задачи одномерной минимизации.
Пусть f(x)-унимодальна на [a;b]. Решим задачу f(x)→min.
Выберем
2 точки:
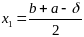 ,
,
 , δ>0.
, δ>0.
точки x1 и x2 располагаются симметрично относительно середины отрезка [a;b]
если f(x1)≤ f(x2), то полагаем a1=a, b1=x2
если f(x1)>f(x2), то полагаем a1=x1, b1=b
В силу унимодальности f(x) [a1;b1] ∩X*≠Ø
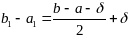
Пусть
найден отрезок [ak-1;bk-1],
длина кот.
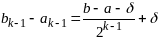 ,
который имеет непустое пересечение с
множеством X*
,
который имеет непустое пересечение с
множеством X*
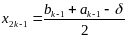 ,
,
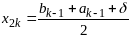
если f(x2k-1)≤f(x2k) полагаем ak=ak-1, bk=x2k.
если f(x2k-1)>f (x2k) полагаем ak=x2k-1, bk=bk-1
Получим отрезок [ak;bk],
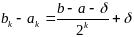 и
который имеет непустое пересеч с X*
и
который имеет непустое пересеч с X*
Процесс
деления отрезка пополам продолж. до тех
пор, пока не будет достигнута заданная
точность ε>0,
т.е. пока не будет выполнено условие
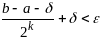
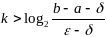
Чтобы достигнуть зад. точность необх. выполнить k делений отрезка пополам. Т.к. на каждом шаге знач. фнкции вычисл. дважды, то кол-во вычислений функции будет равно
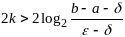
В качестве решения берут точку x2k+1, если f(x2k+1)≤f(x2k+2) и точку x2k+2, если
f(x2k+1)>f(x2k+2)
Если нет необходимости вычисл. приближ. значение min-ма именно в точке, кот. выбрана в качестве решения, то за решение задачи можно взять середину

29.Метод золотого сечения.
МЗС позволяет решить задачу с требуемой точностью при меньшем кол-ве вычислений значения функции.
Опр, Золотым сечением отрезка наз деление отрезка на 2 неравные части так, что отношение длины меньшей части к длине большей равно отношению длины большей части к длине всего отрезка.
Из опр =>, что отрезок [a;b] делиться точками:

Точка х1 дает золотое сечение отрезка [a;x2], а х2 – отрезка [x1;b].
Описание МЗС
Решаем
задачу
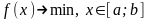 .
Положим а1=а, b1=b
и найдем точки х1 и х2, котор делят [a1;b1]
в золотом сечении. Вычислим
.
Положим а1=а, b1=b
и найдем точки х1 и х2, котор делят [a1;b1]
в золотом сечении. Вычислим
 и
и
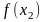 .
Если
.
Если
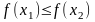 ,
то положим а2=а1, b2=x2,
,
то положим а2=а1, b2=x2,
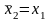 .
.
Если
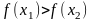 ,
то а2=х1, b2=b1,
,
то а2=х1, b2=b1,
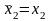 .
Длина построенного отрезка [a2;b2]
равна
.
Длина построенного отрезка [a2;b2]
равна
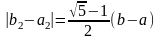 и точка минимума функции принадлежит
[a2;b2].
Пусть на некотор этапе найдены х1,
х2,…,х[n-1]
и найден отр-к
и точка минимума функции принадлежит
[a2;b2].
Пусть на некотор этапе найдены х1,
х2,…,х[n-1]
и найден отр-к
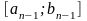 в золотом сечении, его длина
в золотом сечении, его длина
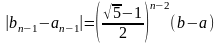 .
Определим т
.
Определим т
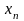 по правилу
по правилу
 .
Возможны 2 случая:
.
Возможны 2 случая:
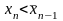 и
и
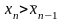 Рассмотрим первый: вычисляем значения
в обеих точках, Если
Рассмотрим первый: вычисляем значения
в обеих точках, Если
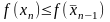 ,
то
,
то
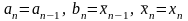 .
Иначе,
.
Иначе,
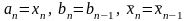 .
Получаем отрезок
.
Получаем отрезок
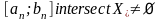 и
и
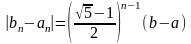 .
И найдем точку
.
И найдем точку
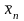 ,
кот делит
,
кот делит
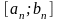 в золотом сечении. Процесс повторяется
до тех пор пока выполняется неравенство
в золотом сечении. Процесс повторяется
до тех пор пока выполняется неравенство
 .
В качестве решения задачи берут точку
и с вычесленным значением функции в
этой точке.
.
В качестве решения задачи берут точку
и с вычесленным значением функции в
этой точке.
Замечание.
Погрешность
этого метода не превышает значение
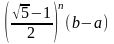
Замечание.
В МЗС сильно возрастает погрешность
при вычислении
по формуле
из-за приблизительности вычислений
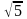 ,
Поэтому на каждом шаге метода надо
выполнять непосредственное деление
отрезка в золотом сечении. И выбирать
в качестве
ту точку, которая дальше от
,
Поэтому на каждом шаге метода надо
выполнять непосредственное деление
отрезка в золотом сечении. И выбирать
в качестве
ту точку, которая дальше от
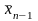 .
.
Замечание. МЗС можно применять для нахождения минимума функций не явл-ся унимодальными. Но в этом случае решение может находиться далеко от глобального минимума.
