34) Необходимый признак сходимости числового ряда (доказать)-
Теорема: Пусть числовой ряд
u1+u2+...+un+... , |
(1) |
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член un стремится к нулю Доказательство. Из условия теоремы имеем
Так как Sn - Sn-1 = un
то
Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство
,
а он, однако не является сходящимся. Так гармонический ряд
,
для которого
,
расходится. Но согласно доказанному необходимому признаку сходимости ряда, если
,
то ряд (1) расходится.
В самом деле, если бы он сходился, то
равнялся
бы нулю.
Таким образом, доказанная
нами теорема иногда позволяет, не
вычисляя суммы Sn,
сделать заключение о расходимости того
или иного ряда. Например, ряд
,
расходится, так как
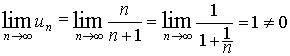
Привести пример расходящегося ряда, для которого выполняется необходимый признак
С
помощью необходимого признака доказать,
что ряд расходится: 
Решение: 
,
,
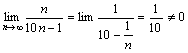ряд расходится.
Рассмотрим достаточные признаки сходимости положительных рядов.
Признак
сравнения 1.Пусть
даны два ряда с положительными
членами 
, 
,
причем каждый член ряда
не
превосходит соответствующего члена
ряда
. 
.Тогда
если сходится ряд
,
то сходится и ряд
;
если расходится ряд
,
то расходится и ряд
.
Что можно сказать о сходимости ряда на основе только необходимого признака…???
35)Определение числового ряда с положительными членами- Такие ряды будем называть положительными рядами.
Теорема 3.1. (признак сравнения)
Пусть даны два положительных ряда
,(3.1) ,3.2)
и выполняются условия для всех n=1,2,…
Тогда: 1) из сходимости ряда (3.2) следует сходимость ряда (3.1);
2) из расходимости ряда (3.1) следует расходимость ряда (3.2).
Доказательство. 1. Пусть ряд (3.2) сходится и его сумма равна В. Последовательность частичных сумм ряда (3.1) является неубывающей ограниченной сверху числом В, т. е.
Определение сходящегося числового ряда-- ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел, т. е.
В этом случае число называется суммой ряда и пишется
.
Признак Коши сходимости числового ряда с положительными членами. Исследовать на сходимость ряд-Предельный признак Коши
Пусть члены положительного ряда (1.1) таковы, что существует предел
Тогда: 1) при q < 1 ряд (1.1) сходится;
2) при q > 1 ряд (1.1) расходится;
3) при q = 1 о сходимости ряда (1.1) ничего сказать нельзя, необходимы дополнительные исследования
Пример 3.6. Исследовать на сходимость ряд
Применим предельный признак Коши:
Следовательно, исходный ряд сходится.
(Интегральный признак Коши).
Пусть
функция f(x)
непрерывная неотрицательная невозрастающая
функция на промежутке
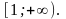
Тогда
ряд
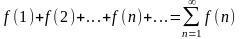и несобственный интеграл
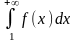сходятся или расходятся одновременно.
Пример 3.7. Исследовать на сходимость гармонический ряд
Применим интегральный признак Коши.
В нашем случае функция удовлетворяет условию теоремы 3.4. Исследуем на сходимость несобственный интеграл
Имеем .
Несобственный интеграл расходится, следовательно, исходный гармонический ряд расходится также.
И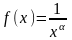
сследуйте
сходимость ряда
.
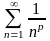П
усть
При x>0 эта функция положительна и не возрастающая.
Е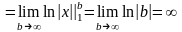
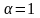сли
Т.е. интеграл и ряд расходятся
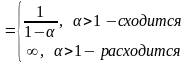
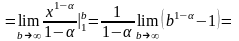
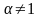
Если
36) Уравнение Бернулли. Обыкновенное дифференциальное уравнение вида:
называется
уравнением
Бернулли
(при
или
получаем
неоднородное или однородное линейное
уравнение). При
является частным случаем уравнения
Риккати.
Метод решения
Первый способ
Разделим все члены уравнения на
получим
Делая замену
и дифференцируя, получаем:
Это уравнение приводится к линейному:
и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя.
Второй способ
Заменим
тогда:
Подберем
так,
чтобы было
для
этого достаточно решить уравнение с
разделяющимися переменными 1-го порядка.
После этого для определения
получаем
уравнение
—
уравнение с разделяющимися переменными.