
- •Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •Необходимое и достаточное условие интегрируемости
- •Интегрируемость непрерывных функций
- •Свойства определенного интеграла (об изменении знака, свойства линейности и аддитивности). Найдите…
- •Определенный интеграл
- •Классы интегрируемых функций.
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом
- •Формула интегрирования по частям.
- •Замена переменной в определенном интеграле.
- •Площадь криволинейной трапеции.
- •17. Интеграл по симметричному промежутку для четной и нечетной функции
- •18. Вычисление площадей фигур с помощью определенного интеграла. Вывод формулы.
- •19. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Вывод формулы.
- •20. Вычисление объема тела по площади поперечного сечения. Объем тела вращения. Вывод формулы.
- •21) Несобственные интегралы по бесконечному промежутку.
- •25,26) Двойные интегралы Определение и основные свойства
- •Свойства интегрируемых функций и двойных интегралов. Аддитивность.
- •Линейность.
- •Оценка модуля интеграла.
- •27) Вычисление двойного интеграла Приведение двойного интеграла к повторному в случае прямоугольной области.
- •28. Полярная система координат и переход к ней под знаком двойного интеграла.
- •34) Необходимый признак сходимости числового ряда (доказать)-
- •37) Лнду (Метод Лагранжа).
- •38) Дифференциальные уравнения высшего порядка, допускающие понижение порядка.
- •39) Однородные дифференциальные уравнения первого порядка: определение, методы решения.
- •40) Линейные неоднородные дифференциальные уравнения первого порядка: определение, методы решения.
- •41) Линейные неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами и специальной правой частью.
- •42)Дифференциальные уравнения в полных дифференциалах: определение, метод решения.
- •Теорема.
- •43) Дифференциальные уравнения с разделяющимися переменными: определение, решение.
- •44) Дифференциальные уравнения первого порядка: определение, общее решение, теорема единственности, задача Коши. Решить задачу Коши для дифференциального уравнения…
- •Теорема существования и единственности решения задачи Коши
21) Несобственные интегралы по бесконечному промежутку.
Рассмотрим
функцию ![]() определенную
и непрерывную на промежутке
определенную
и непрерывную на промежутке ![]() .
Очевидно, определение определенного
интеграла на таком промежутке бессмысленно.
Предположим, что данная функция
интегрируема
на любом конечном промежутке вида [a,
A]. Тогда интегралом от этой функции по
бесконечному
.
Очевидно, определение определенного
интеграла на таком промежутке бессмысленно.
Предположим, что данная функция
интегрируема
на любом конечном промежутке вида [a,
A]. Тогда интегралом от этой функции по
бесконечному
промежутку
назовем  .
Обозначать этот интеграл будем как
.
Обозначать этот интеграл будем как 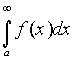 .
Таким образом
.
Таким образом
=
Эталонный
интеграл.
интеграл

Если
![]() ,
то подынтегральная функция
,
то подынтегральная функция
![]() стремится
к
стремится
к
![]() при
при
![]() ,
так что получается несобственный
интеграл второго рода.
,
так что получается несобственный
интеграл второго рода.
Рассмотрим такие случаи:
1)
![]() .
Тогда интеграл вычисляется так:
.
Тогда интеграл вычисляется так:
 поскольку
при
поскольку
при
![]() имеем
имеем
![]() и
и
![]()
2)
![]() .
Тогда
.
Тогда
 то
есть интеграл расходится, поскольку
то
есть интеграл расходится, поскольку
![]() при
.
при
.
3)
![]() .
Тогда
.
Тогда
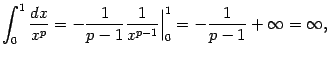 и
интеграл снова расходится, поскольку
и
интеграл снова расходится, поскольку
![]() при
,
если показатель
при
,
если показатель
![]() .
.
22) Свойства несобственных интегралов.
А) Признак сравнения несобственных интегралов 1 рода. Если 0 меньше (или равен) f(x) меньше (или равна) g(x) на промежутке [0;+ бесконечности], то:
Из
сходимости
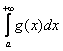 следует
сходимость
следует
сходимость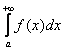 .
.
Из расходимости следует расходимость .
Теорема очевидна из геометрического смысла.
Б) Признак абсолютной сходимости несобственного интеграла 1 рода.
Если
несобственный интеграл 1 рода
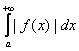 сходится,
то
тоже
сходится.
сходится,
то
тоже
сходится.
Следует из первого свойства.
23)Абсолютная сходимость несобственных интегралов по бесконечному промежутку.
![]() Опр.
1.Если
сходится интеграл
Опр.
1.Если
сходится интеграл
 ,
то интеграл
,
то интеграл
 называется
сходящимся абсолютно. Если сходится
интеграл
,
а интеграл
расходится,
то интеграл
называется
сходящимся условно.
Примеры
исследования интегралов на абсолютную
сходимость:
15.
называется
сходящимся абсолютно. Если сходится
интеграл
,
а интеграл
расходится,
то интеграл
называется
сходящимся условно.
Примеры
исследования интегралов на абсолютную
сходимость:
15.
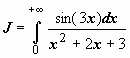 .
.
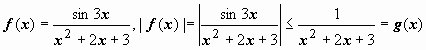 ;
интеграл от большей функции сходится,
следовательно,
;
интеграл от большей функции сходится,
следовательно,
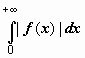 сходится,
следовательно, исходный интеграл
сходится абсолютно.
16.
сходится,
следовательно, исходный интеграл
сходится абсолютно.
16.
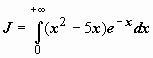 .
.
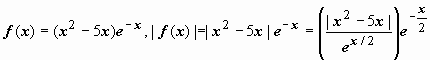 ,
первый множитель,
,
первый множитель,
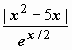 ,
стремится к нулю при
,
стремится к нулю при
![]() ,
следовательно, ограничен:
,
следовательно, ограничен:
 ,
интеграл от последней функции сходится,
следовательно, исходный интеграл
сходится абсолютно.
Приведённые
примеры показывают, что переход от
к
и
применение к последнему интегралу
методов исследования на сходимость
несобственных интегралов от неотрицательных
функций, в случае его сходимости,
позволяет сделать вывод и о сходимости
(притом, абсолютной) исходного интеграла.
Если же интеграл от | f(x)|
расходится, решение задач значительно
усложняется.
Пример:
исследовать на сходимость интеграл
,
интеграл от последней функции сходится,
следовательно, исходный интеграл
сходится абсолютно.
Приведённые
примеры показывают, что переход от
к
и
применение к последнему интегралу
методов исследования на сходимость
несобственных интегралов от неотрицательных
функций, в случае его сходимости,
позволяет сделать вывод и о сходимости
(притом, абсолютной) исходного интеграла.
Если же интеграл от | f(x)|
расходится, решение задач значительно
усложняется.
Пример:
исследовать на сходимость интеграл
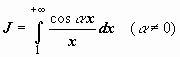 .
1.
Докажем, что этот интеграл сходится.
Интегрируем его по частям:
.
1.
Докажем, что этот интеграл сходится.
Интегрируем его по частям:
 .
.
Для
последнего интеграла
![]() ,
т.е. он сходится абсолютно, следовательно,
исходный интеграл сходится.
2.
Докажем, что для исходного интеграла
абсолютной сходимости нет, т.е. что
,
т.е. он сходится абсолютно, следовательно,
исходный интеграл сходится.
2.
Докажем, что для исходного интеграла
абсолютной сходимости нет, т.е. что
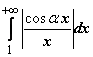 расходится.
Так как
расходится.
Так как
![]() ,
то
,
то
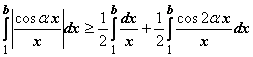 ,
для последнего интеграла, по доказанному
выше, существует конечный предел при
,
для последнего интеграла, по доказанному
выше, существует конечный предел при
![]() ,
для предыдущего - нет, следовательно,
расходится.
Вывод
- исходный интеграл сходится условно.
,
для предыдущего - нет, следовательно,
расходится.
Вывод
- исходный интеграл сходится условно.
Установить
условную сходимость несобственного
интеграла по бесконечному промежутку
при отсутствии абсолютной сходимости
позволяют два следующих признака:
признак
сходимости Абеля:
1.
пусть функции f(x)
и g(x)
определены в промежутке
![]() ,
причём f(x)
интегрируема в этом промежутке, т.е.
интеграл
сходится
(условно или абсолютно);
2.
g(x)
монотонна и ограничена:
,
причём f(x)
интегрируема в этом промежутке, т.е.
интеграл
сходится
(условно или абсолютно);
2.
g(x)
монотонна и ограничена:
![]() .
Тогда интеграл
.
Тогда интеграл
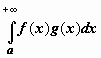 сходится.
признак
сходимости Дирихле:
1.
пусть функция f(x)
интегрируема в любом конечном промежутке
[a,
b],
и интеграл по этому промежутку ограничен
(как функция верхнего предела b):
сходится.
признак
сходимости Дирихле:
1.
пусть функция f(x)
интегрируема в любом конечном промежутке
[a,
b],
и интеграл по этому промежутку ограничен
(как функция верхнего предела b):
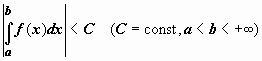 ;
2.
g(x)
монотонно стремится к нулю при
;
2.
g(x)
монотонно стремится к нулю при
![]() :
:
![]() .
Тогда интеграл
сходится.
Применим,
например, признак Дирихле к
.
Здесь f(x)
= cos x,
g(x)
= 1/x,
условия признака выполнены, поэтому
интеграл сходится условно.
.
Тогда интеграл
сходится.
Применим,
например, признак Дирихле к
.
Здесь f(x)
= cos x,
g(x)
= 1/x,
условия признака выполнены, поэтому
интеграл сходится условно.
24) Несобственные интегралы 2 рода.
Определение 1.
Интеграл
вида:
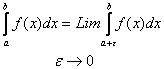 ,
где y=f(x) непрерывна (a;b], a - точка разрыва
2 рода. Называется несобственным
интегралом 2 рода.
,
где y=f(x) непрерывна (a;b], a - точка разрыва
2 рода. Называется несобственным
интегралом 2 рода.
Если предел конечен, то несобственный интеграл 2 рода называется сходящимся.
Определение 2.
Если предел равен бесконечности или не существует вовсе, то несобственный интеграл 2 рода называется расходящимся.
Пусть функция y=f(x) имеет разрыв 2 рода в точке C, принадлежащей (a;b). В остальных точках промежутка непрерывна.
Определение 3.
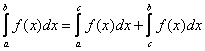
Если оба несобственных интеграла 2 рода справа сходятся, то несобственный интеграл слева называется сходящимся.
Если хотя бы один из интегралов справа расходится, то несобственный интеграл слева называется расходящимся.
интеграл

Если
![]() ,
то подынтегральная функция
,
то подынтегральная функция
![]() стремится
к
стремится
к
![]() при
при
![]() ,
так что получается несобственный
интеграл второго рода.
,
так что получается несобственный
интеграл второго рода.
Рассмотрим такие случаи:
1)
![]() .
Тогда интеграл вычисляется так:
.
Тогда интеграл вычисляется так:
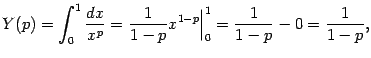 поскольку
при
поскольку
при
![]() имеем
имеем
![]() и
и
![]()
2)
![]() .
Тогда
.
Тогда
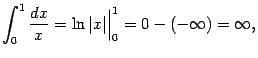 то
есть интеграл расходится, поскольку
то
есть интеграл расходится, поскольку
![]() при
.
при
.
3)
![]() .
Тогда
.
Тогда
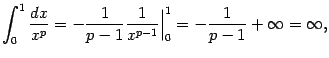 и
интеграл снова расходится, поскольку
и
интеграл снова расходится, поскольку
![]() при
,
если показатель
при
,
если показатель
![]() .
.
