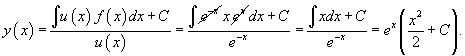- •Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •Необходимое и достаточное условие интегрируемости
- •Интегрируемость непрерывных функций
- •Свойства определенного интеграла (об изменении знака, свойства линейности и аддитивности). Найдите…
- •Определенный интеграл
- •Классы интегрируемых функций.
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом
- •Формула интегрирования по частям.
- •Замена переменной в определенном интеграле.
- •Площадь криволинейной трапеции.
- •17. Интеграл по симметричному промежутку для четной и нечетной функции
- •18. Вычисление площадей фигур с помощью определенного интеграла. Вывод формулы.
- •19. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Вывод формулы.
- •20. Вычисление объема тела по площади поперечного сечения. Объем тела вращения. Вывод формулы.
- •21) Несобственные интегралы по бесконечному промежутку.
- •25,26) Двойные интегралы Определение и основные свойства
- •Свойства интегрируемых функций и двойных интегралов. Аддитивность.
- •Линейность.
- •Оценка модуля интеграла.
- •27) Вычисление двойного интеграла Приведение двойного интеграла к повторному в случае прямоугольной области.
- •28. Полярная система координат и переход к ней под знаком двойного интеграла.
- •34) Необходимый признак сходимости числового ряда (доказать)-
- •37) Лнду (Метод Лагранжа).
- •38) Дифференциальные уравнения высшего порядка, допускающие понижение порядка.
- •39) Однородные дифференциальные уравнения первого порядка: определение, методы решения.
- •40) Линейные неоднородные дифференциальные уравнения первого порядка: определение, методы решения.
- •41) Линейные неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами и специальной правой частью.
- •42)Дифференциальные уравнения в полных дифференциалах: определение, метод решения.
- •Теорема.
- •43) Дифференциальные уравнения с разделяющимися переменными: определение, решение.
- •44) Дифференциальные уравнения первого порядка: определение, общее решение, теорема единственности, задача Коши. Решить задачу Коши для дифференциального уравнения…
- •Теорема существования и единственности решения задачи Коши
39) Однородные дифференциальные уравнения первого порядка: определение, методы решения.
Определение
1.
Уравнение 1-го порядка
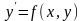 называется однородным,
если для его правой части при любых
называется однородным,
если для его правой части при любых
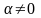 справедливо соотношение
справедливо соотношение
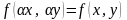 ,
называемое условием
однородности функции
двух переменных нулевого измерения.
,
называемое условием
однородности функции
двух переменных нулевого измерения.
Пример
1.
Показать, что функция
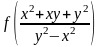 – однородная нулевого измерения.
– однородная нулевого измерения.
Решение.
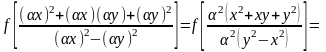
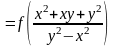 ,
,
,
,
что и требовалось доказать.
Теорема.
Любая функция
 – однородна и, наоборот, любая однородная
функция
– однородна и, наоборот, любая однородная
функция
 нулевого измерения приводится к виду
нулевого измерения приводится к виду
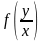 .
.
Доказательство.
Первое
утверждение теоремы очевидно, так как
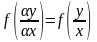 .
Докажем второе утверждение. Положим
.
Докажем второе утверждение. Положим
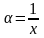 ,
тогда для однородной функции
,
тогда для однородной функции
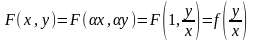 ,
,
что и требовалось доказать.
Определение 2. Уравнение
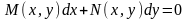 , (4.1)
, (4.1)
где
M
и
N
–
однородные функции одной и той же
степени, т.е. обладают свойством
 при всех
при всех
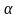 ,
называется однородным.
,
называется однородным.
Очевидно, что уравнение (4.1) всегда может быть приведено к виду
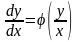 , (4.2)
, (4.2)
хотя для его решения можно этого и не делать.
Однородное
уравнение (4.1) приводится к уравнению с
разделяющимися переменными с помощью
замены искомой функции y
по формуле
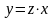 ,
где
,
где
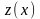 –
новая искомая функция. Выполнив эту
замену в уравнении (4.2), получим:
–
новая искомая функция. Выполнив эту
замену в уравнении (4.2), получим:
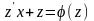 (4.3)
(4.3)
или
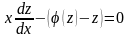 ,
,
т.е.
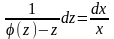 .
.
Интегрируя последнее равенство, получаем общий интеграл уравнения (4.3) относительно функции
 ,
,
который
после повторной замены
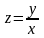 даёт общий интеграл исходного уравнения
(4.2). Кроме того, если
даёт общий интеграл исходного уравнения
(4.2). Кроме того, если
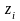 – корни уравнения
– корни уравнения
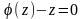 ,
то функции
,
то функции
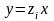 (где
(где
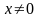 )
– решения однородного уравнения (4.2).
Если же
)
– решения однородного уравнения (4.2).
Если же
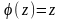 ,
то уравнение (4.2) принимает вид
,
то уравнение (4.2) принимает вид
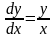
и становится уравнением с разделяющимися переменными. Его решениями являются функции, определяющие на плоскости полупрямые:
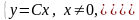 .
.
Замечание.
Иногда целесообразно вместо указанной
выше замены использовать замену
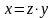 .
.
40) Линейные неоднородные дифференциальные уравнения первого порядка: определение, методы решения.
Определение линейного уравнения первого порядка
Дифференциальное уравнение вида
![]()
где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
Использование интегрирующего множителя;
Метод вариации постоянной.
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
то интегрирующий множитель определяется формулой:
![]()
Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x). Общее решение диффференциального уравнения выражается в виде:
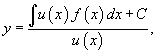
где C − произвольная постоянная.
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
![]()
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Задача Коши
Если, кроме дифференциального уравнения, задано также начальное условие в форме y(x0) = y0, то такая задача называется задачей Коши. Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие y(x0) = y0.
Пример 1
Решить уравнение y' − y − xex = 0.
Решение.
Запишем данное уравнение в стандартной форме:
![]()
Будем решать это уравнение, используя интегрирующий множитель:
![]()
Тогда общее решение линейного дифференциального уравнения определяется выражением: