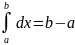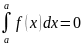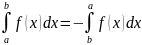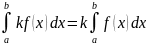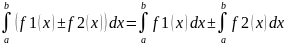10. Свойства определенного интеграла (об изменении знака, свойства линейности и аддитивности). Найдите…

1. 

2. 

3. 

4. 

5. 

6. Аддитивность

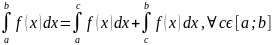
7. Если f(x) –четная функция=>

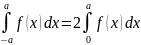
8. Если f(x) –нечетная функция=>

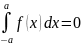
9. Если f(x) ≥0 на [a;b] =>

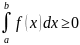
10. Монотонность. Если

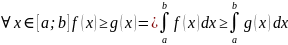
11. Теорема об оценке определенного интеграла. Если m-наименьшее, М-наибольшее значение функции y=f(x) на [a;b], тогда

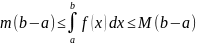, где a < b

Док-во: т.к. функция y=f(x) непрерывна на [a;b], то по т.Вейерштрасса она достигает своего наименьшего значения m и наибольшего М, т.е.

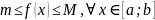
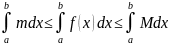по свойству 4: =>

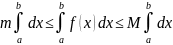по свойству 1: чтд.

12. Теорема о среднем:

Если y=f(x) непрерывна на [a;b], то Ǝ т.ξ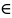 [a;b] такая, что выполняется равенство: 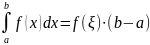, f(ξ) называют средним значением функции y=f(x) на [a;b] =>

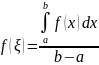
Определенный интеграл

Определение. Разбиением 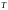отрезка 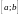называется набор точек 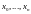этого отрезка такой, что .

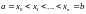Отрезки 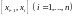называются отрезками разбиения.

Максимум из длин отрезков разбиения называется параметром разбиения.

Определение. Разбиением с отмеченными точками 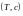называется разбиение и набор точек .

Определение. Пусть функция 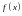определена на отрезке 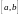, а - разбиение с отмеченными точками этого отрезка. Сумма

,

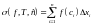где , называется интегральной суммой функции 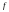, соответствующей разбиению с отмеченными точками .

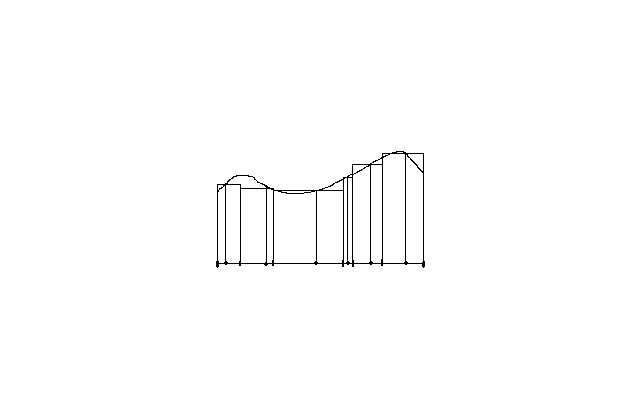
a=x₀ c₁ x₁ c₂ x_{2 ………………………………………………..} x_n-1 c_n x_n=b

Определение. Говорят, что число 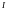является интегралом Римана от функции на отрезке , если для любого 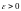найдется такое 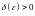, что для любого разбиения с отмеченными точками отрезка , параметр разбиения которого , имеет место соотношение

.

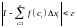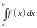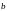Интеграл от функции по отрезку обозначается символом , числа и называются верхним и нижним пределом интегрирования соответственно;

- подынтегральная функция, 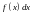- подынтегральное выражение, - переменная интегрирования.

Таким образом,

.

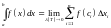Определение. Функция называется интегрируемой на отрезке , если для нее определен интеграл Римана.

Необходимое условие интегрируемости.

Утверждение. Если функция , определенная на отрезке , интегрируема на нем, то она ограничена на этом отрезке.

Классы интегрируемых функций.

Теорема. Если функция непрерывна на отрезке , то она интегрируема на нем.

(без доказательства)

Теорема. Если ограниченная на отрезке функция имеет на нем лишь конечное число точек разрыва первого рода, то она интегрируема на этом отрезке.

(без доказательства)

Пример. Функция 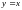непрерывна на отрезке 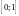, а значит, интегрируема на нем. Интеграл 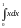будет пределом любой последовательности интегральных сумм с 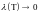. Рассмотрим последовательность разбиений на равные отрезки: 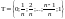и выделим точки 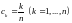. Тогда

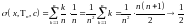при 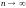. То есть .

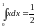Свойства определенного интеграла

Пусть функция интегрируема на отрезке 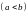. Положим по определению 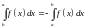и .

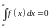(Аддитивность). Пусть ограниченная кусочно-непрерывная функция определена в наибольшем из промежутков , 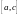и 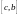. Тогда справедливо равенство

.

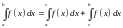Пояснение. Предположим сначала, что 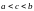. Рассмотрим разбиение отрезка на части. Не нарушая общности, можно считать точку одной из точек деления. Для соответствующей интегральной суммы будем иметь

.

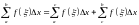Переходя к пределу при , получим требуемое равенство.

Другие случаи взаимного расположения точек приводятся к разобранному. Пусть, например, 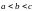. Тогда, по доказанному,

,

.

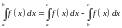После перестановки пределов интегрирования в последнем интеграле, получим нужное нам равенство.

Аналогично поступаем с другими расположениями.

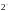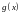(Линейность). Пусть функции и интегрируемы на отрезке . Тогда произвольная линейная комбинация этих функций также будет интегрируемой на этом отрезке, причем

.

Пояснение. Возьмем произвольное разбиение отрезка на части и составим интегральные суммы для всех трех интегралов. При этом точки в каждом частичном промежутке выбираем для всех трех сумм одни и те же. Получим

.

Переходя в последнем равенстве к пределу при 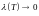, убеждаемся в интегрируемости линейной комбинации и справедливости требуемого равенства.

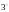Теорема (об оценке модуля интеграла). Пусть функция интегрируема на отрезке , тогда функция 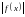также интегрируема на этом отрезке, и имеет место неравенство

.

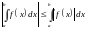Пояснение. Для доказательства нужного нам неравенства для интегралов перейдем к пределу в соответствующем неравенстве для интегральных сумм.

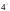Теорема (об интегрировании неравенств). Если функции и интегрируемы на отрезке и 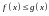везде на , то

.

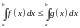Доказательство. Так как функции и интегрируемы, то мы можем выбрать любую последовательность разбиений с параметрами, стремящимися к нулю, для того, чтобы в пределе получить интеграл. Выберем для обеих функций одинаковые разбиения 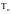отрезка , также одинаковые наборы выделенных точек 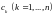. Тогда, с учетом заданного неравенства, имеем:

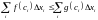
и, переходя в последним неравенстве к пределу при , получаем нужное нам неравенство.

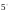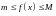Теорема (об оценке интеграла). Если функция интегрируема на отрезке , и если на всем этом отрезке справедливо неравенство , то

.

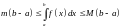Доказательство. Воспользуемся предыдущим свойством с учетом того, что

.

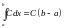Теорема о среднем значении

Определение. Средним интегральным функции на отрезке называется число

.

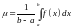Теорема (о среднем интегральном). Пусть функция интегрируема на отрезке , и пусть на всем этом отрезке . Тогда

,

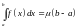где .

Доказательство. По теореме об оценке интеграла

,

откуда получаем 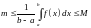. Теперь полагаем

.

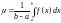В случае непрерывной функции справедлива следующая теорема.

Теорема (о среднем интегральном значении непрерывной функции). Пусть функция непрерывна на отрезке . Тогда найдется точка 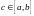такая, что

.

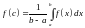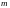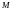Доказательство. В качестве и возьмем соответственно наименьшее и наибольшее значение функции на отрезке . По второй теореме Вейерштрасса эти значения принимаются в некоторых точках :

.

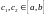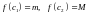По теореме о среднем интегральном 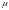принадлежит отрезку с 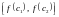. По теореме же Коши о промежуточном значении непрерывной функции на отрезке с концами в точках и найдется точка , принадлежащая этому отрезку, в которой .

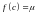Требование непрерывности функции на существенно. В самом деле, рассмотрим 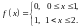Тогда 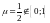(множеству значений функции