
- •Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •Необходимое и достаточное условие интегрируемости
- •Интегрируемость непрерывных функций
- •Свойства определенного интеграла (об изменении знака, свойства линейности и аддитивности). Найдите…
- •Определенный интеграл
- •Классы интегрируемых функций.
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом
- •Формула интегрирования по частям.
- •Замена переменной в определенном интеграле.
- •Площадь криволинейной трапеции.
- •17. Интеграл по симметричному промежутку для четной и нечетной функции
- •18. Вычисление площадей фигур с помощью определенного интеграла. Вывод формулы.
- •19. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Вывод формулы.
- •20. Вычисление объема тела по площади поперечного сечения. Объем тела вращения. Вывод формулы.
- •21) Несобственные интегралы по бесконечному промежутку.
- •25,26) Двойные интегралы Определение и основные свойства
- •Свойства интегрируемых функций и двойных интегралов. Аддитивность.
- •Линейность.
- •Оценка модуля интеграла.
- •27) Вычисление двойного интеграла Приведение двойного интеграла к повторному в случае прямоугольной области.
- •28. Полярная система координат и переход к ней под знаком двойного интеграла.
- •34) Необходимый признак сходимости числового ряда (доказать)-
- •37) Лнду (Метод Лагранжа).
- •38) Дифференциальные уравнения высшего порядка, допускающие понижение порядка.
- •39) Однородные дифференциальные уравнения первого порядка: определение, методы решения.
- •40) Линейные неоднородные дифференциальные уравнения первого порядка: определение, методы решения.
- •41) Линейные неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами и специальной правой частью.
- •42)Дифференциальные уравнения в полных дифференциалах: определение, метод решения.
- •Теорема.
- •43) Дифференциальные уравнения с разделяющимися переменными: определение, решение.
- •44) Дифференциальные уравнения первого порядка: определение, общее решение, теорема единственности, задача Коши. Решить задачу Коши для дифференциального уравнения…
- •Теорема существования и единственности решения задачи Коши
Интеграл с переменным верхним пределом
Пусть функция интегрируема на отрезке . Определим на этом же отрезке функцию
 ,
,
которую
часто называют интегралом с переменным
верхним пределом. Из свойства аддитивности
определенного интеграла вытекает
корректность определения функции
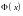 для
для
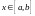 .
.
Теорема (о непрерывности интеграла с переменным верхним пределом). Если функция интегрируема на отрезке , то функция будет непрерывной на этом отрезке.
Доказательство.
Интегрируемая
на отрезке функция ограничена на нем,
то есть существует такое число
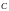 ,
что
,
что
 на
.
Пусть
,
и пусть
на
.
Пусть
,
и пусть
 - приращение независимой переменной,
при котором
- приращение независимой переменной,
при котором
 .
Воспользовавшись свойством аддитивности,
а также теоремами об оценках определенного
интеграла, получим
.
Воспользовавшись свойством аддитивности,
а также теоремами об оценках определенного
интеграла, получим
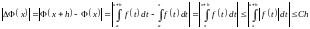 .
.
То
есть
 ,
что означает непрерывность функции
в точке
.
,
что означает непрерывность функции
в точке
.
Теорема (о дифференцируемости интеграла с переменным верхним пределом). Пусть функция непрерывна на отрезке . Тогда функция будет дифференцируемой на этом отрезке.
Доказательство.
 ,
,
где
лежит между
и
 .
Из непрерывности
следует, что при
.
Из непрерывности
следует, что при
 будет справедливо
будет справедливо
 .
.
Основная формула интегрального исчисления.
Доказанная
выше теорема означает, что для непрерывной
на
функции
интеграл
будет первообразной функцией. Если
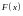 какая-либо другая первообразная
,
то
какая-либо другая первообразная
,
то
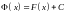 .
Имеем
.
Имеем
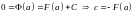 ,
,
поэтому
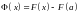 .
При
.
При
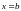 получим
получим
 .
.
Это - формула Ньютона-Лейбница, - основная формула интегрального исчисления.
Мы можем вычислять определенный интеграл, не используя интегральные суммы.
Пример
1.
 .
.
Пример
2. Среднее интегральное значение функции
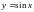 на отрезке
на отрезке
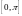
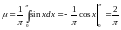 .
.
Формула интегрирования по частям.
Теорема.
Если функции
 и
и
 непрерывно дифференцируемы на отрезке
,
то справедливо соотношение
непрерывно дифференцируемы на отрезке
,
то справедливо соотношение
 .
.
Доказательство. По правилу дифференцирования производной произведения имеем
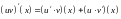 .
.
По условию все функции в этом равенстве непрерывны, а, значит, и интегрируемы на отрезке . Используя линейность интеграла и формулу Ньютона-Лейбница, получаем
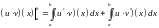 .
.
Пример
3.
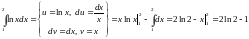 .
.
Замена переменной в определенном интеграле.
Теорема.
Если
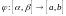 - непрерывно дифференцируемое отображение
отрезка
- непрерывно дифференцируемое отображение
отрезка
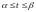 в отрезок
в отрезок
 такое, что
такое, что
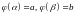 ,
то при любой непрерывной на
функции
справедливо равенство
,
то при любой непрерывной на
функции
справедливо равенство
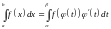 .
.
Доказательство.
Пусть
- первообразная функции
,
тогда по теореме о дифференцировании
сложной функции, функция
 будет первообразной для функции
будет первообразной для функции
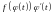 .
По формуле Ньютона-Лейбница получаем
.
По формуле Ньютона-Лейбница получаем
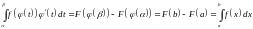 .
.
Пример
4. 

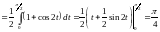 .
.
Геометрические приложения определенного интеграла.
Длина плоской кривой.
Длина кривой, заданной параметрически.
Определение.
Длиной кривой
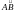 называется точная верхняя граница
называется точная верхняя граница
 для множества периметров
для множества периметров
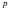 вписанных в кривую ломаных:
вписанных в кривую ломаных:
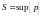 .
Если это число конечно, то кривая
называется спрямляемой.
.
Если это число конечно, то кривая
называется спрямляемой.
Рассмотрим параметрически заданную гладкую кривую

(функции
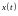 и
и
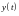 непрерывно дифференцируемы на
непрерывно дифференцируемы на
 ).
).
Утверждение. Параметрически заданная на конечном промежутке гладкая кривая спрямляема.
Формула дли вычисления длины дуги гладкой кривой, заданной параметрически:
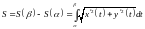 .
.
Пример 1. Найти длину одной арки циклоиды
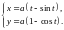
 .
.
Решение: 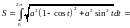
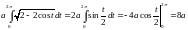 .
.
Длина кривой, заданной явно.
Теперь
рассмотрим гладкуя кривую, заданную
явно графиком функции
 , непрерывно дифференцируемой на отрезке
:
, непрерывно дифференцируемой на отрезке
:
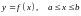 .
.
Утверждение. Явно заданная на конечном промежутке гладкая кривая спрямляема.
Формула дли вычисления длины дуги гладкой кривой, заданной явно:
 .
.
Пример
2. Найти длину дуги кривой
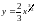 от
от
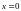 до
до
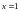 .
.
Решение:
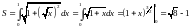 .
.
Площадь плоской фигуры.
Пусть
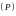 - произвольная фигура на плоскости.
Обозначим через
- произвольная фигура на плоскости.
Обозначим через
 Многоугольники, целиком содержащиеся
в
,
а через
Многоугольники, целиком содержащиеся
в
,
а через
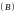 - многоугольники, содержащие
.
Через
- многоугольники, содержащие
.
Через
 и
и
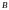 обозначим их площади. Имеем
обозначим их площади. Имеем
 .
Ограниченное сверху множество чисел
имеет точную верхнюю грань
.
Ограниченное сверху множество чисел
имеет точную верхнюю грань
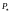 ,
а ограниченное снизу
,
а ограниченное снизу
Множество
чисел
точную нижнюю грань
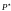 .
Очевидно, что
.
Очевидно, что
 ,
если же эти числа совпадают, то общее
их значение
,
если же эти числа совпадают, то общее
их значение
 называют площадью фигуры
,
а саму эту фигуру называют квадрируемой.
называют площадью фигуры
,
а саму эту фигуру называют квадрируемой.
