
- •Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •Необходимое и достаточное условие интегрируемости
- •Интегрируемость непрерывных функций
- •Свойства определенного интеграла (об изменении знака, свойства линейности и аддитивности). Найдите…
- •Определенный интеграл
- •Классы интегрируемых функций.
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом
- •Формула интегрирования по частям.
- •Замена переменной в определенном интеграле.
- •Площадь криволинейной трапеции.
- •17. Интеграл по симметричному промежутку для четной и нечетной функции
- •18. Вычисление площадей фигур с помощью определенного интеграла. Вывод формулы.
- •19. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Вывод формулы.
- •20. Вычисление объема тела по площади поперечного сечения. Объем тела вращения. Вывод формулы.
- •21) Несобственные интегралы по бесконечному промежутку.
- •25,26) Двойные интегралы Определение и основные свойства
- •Свойства интегрируемых функций и двойных интегралов. Аддитивность.
- •Линейность.
- •Оценка модуля интеграла.
- •27) Вычисление двойного интеграла Приведение двойного интеграла к повторному в случае прямоугольной области.
- •28. Полярная система координат и переход к ней под знаком двойного интеграла.
- •34) Необходимый признак сходимости числового ряда (доказать)-
- •37) Лнду (Метод Лагранжа).
- •38) Дифференциальные уравнения высшего порядка, допускающие понижение порядка.
- •39) Однородные дифференциальные уравнения первого порядка: определение, методы решения.
- •40) Линейные неоднородные дифференциальные уравнения первого порядка: определение, методы решения.
- •41) Линейные неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами и специальной правой частью.
- •42)Дифференциальные уравнения в полных дифференциалах: определение, метод решения.
- •Теорема.
- •43) Дифференциальные уравнения с разделяющимися переменными: определение, решение.
- •44) Дифференциальные уравнения первого порядка: определение, общее решение, теорема единственности, задача Коши. Решить задачу Коши для дифференциального уравнения…
- •Теорема существования и единственности решения задачи Коши
28. Полярная система координат и переход к ней под знаком двойного интеграла.
Переход к полярным координатам в двойном интеграле . Полярная система координат состоит из луча Or . Любая точка M ≠ O однозначно определяется полярным углом φ (0 ≤ φ <2π или –π < φ π) и полярным радиусом r (r≥0) (рис. 4а). Для начала координат O радиус r = 0, а полярный угол не определен.
Пусть декартова полуось Ox совпадает с полярным лучом Or (рис.4а).
Декартовы координаты выражаются через полярные по формулам
![]() (9)
(9)
Полярные координаты выражаются через декартовы:
Пусть область D в декартовых координатах преобразуется в область Dr в полярных координатах согласно формулам (10). Тогда интеграл (1) преобразуется в двойной интеграл в полярных координатах по формуле
Двойной интеграл (11) вычисляется переходом к повторному интегралу в полярных координатах . Пусть область Dr имеет вид (рис. 4б) Dr = { (r, φ ) : α ≤ φ ≤ β, r1(φ) ≤ r≤ r2 (φ)}, где лучи φ = α и φ = β ограничивают сектор, в котором находится фигура Dr , кривые r = r1(φ), r = r2 (φ) ограничивают ее в этом секторе. Тогда
29. Определение числового ряда с положительными членами, его суммы. Определение сходящегося числового ряда. Необходимый признак сходимости числового ряда с положительными членами.
Числовым рядом или
просто рядом называется
выражение ( сумма ) вида
Ряд
называется сходящимся , если
последовательность его частичных сумм
|
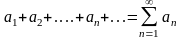 .
.
Числа
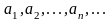 называются членами ряда,
называются членами ряда,
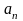 –
общим или n–м
членом ряда.
–
общим или n–м
членом ряда.
Чтобы
задать ряд достаточно задать функцию
натурального аргумента
 вычисления
вычисления
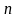 -го
члена ряда по его номеру
-го
члена ряда по его номеру

Определение сходящегося числового ряда- ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел, т. е.

В этом случае число называется суммой ряда и пишется
 .
.
Признак Даламбера сходимости числового ряда с положительными членами-
Предельный признак Даламбера
Пусть члены положительного ряда таковы, что существует предел
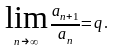 Тогда:
1) при q
< 1 ряд (1.1) сходится;
Тогда:
1) при q
< 1 ряд (1.1) сходится;
2) при q > 1 ряд (1.1) расходится;
3) при q = 1 о сходимости ряда) ничего сказать нельзя, необходимы дополнительные исследования.
Замечание:
Ряд будет расходиться и в том случае,
когда
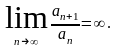 Пример
Исследовать на сходимость ряд
Пример
Исследовать на сходимость ряд
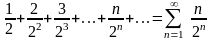 .
.
Применим предельный признак Даламбера.
В
нашем случае
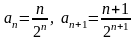 .
.
Тогда
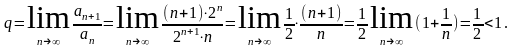
Следовательно, исходный ряд сходится.
31) Определение числового ряда с положительными членами, его суммы- Такие ряды будем называть положительными рядами.
Теорема 3.1. (признак сравнения)
Пусть даны два положительных ряда
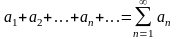 ,(3.1)
,(3.1)
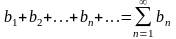 ,3.2)
,3.2)
и
выполняются условия
 для всех n=1,2,…
для всех n=1,2,…
Тогда: 1) из сходимости ряда (3.2) следует сходимость ряда (3.1);
2) из расходимости ряда (3.1) следует расходимость ряда (3.2).
Доказательство. 1. Пусть ряд (3.2) сходится и его сумма равна В. Последовательность частичных сумм ряда (3.1) является неубывающей ограниченной сверху числом В, т. е.
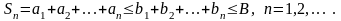
Определение расходящегося числового ряда- Ряд называется расходящимся, если последовательность его частичных сумм не имеет конечного предела.
Расходящемуся ряду не приписывают никакой суммы.
Таким образом, задача нахождения суммы сходящегося ряда (1.1) равносильна вычислению предела последовательности его частичных сумм.
Рассмотрим несколько примеров. Пример 1.4. Доказать, что ряд
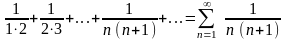 сходится,
и найти его сумму.
сходится,
и найти его сумму.
Найдем
n-ю
частичную сумму данного ряда
 .
.
Общий
член
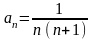 ряда представим в виде
ряда представим в виде
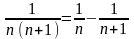 .
.
Тогда

Отсюда
имеем:
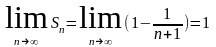 .
Следовательно, данный ряд сходится и
его сумма равна 1:
.
Следовательно, данный ряд сходится и
его сумма равна 1:
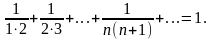
Достаточный
признак расходимости числового ряда с
положительными членами-
Если общий член ряда
 не стремится к нулю при
не стремится к нулю при
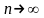 ,
то этот ряд расходится.
,
то этот ряд расходится.
Пример 2.2. Исследовать на сходимость ряд
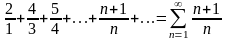 .
.
Для
этого ряда
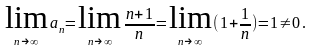
Следовательно, данный ряд расходится.
Рассмотренные
выше расходящиеся ряды (1.6), (1.7) также
являются таковыми в силу того, что для
них не выполняется необходимый признак
сходимости. Для ряда (1.6) предел
Для ряда (1.6) предел
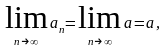 для ряда (1.7) предел
для ряда (1.7) предел
 не существует.
не существует.
32) Определение числового ряда с положительными членами-- Такие ряды будем называть положительными рядами.
Теорема 3.1. (признак сравнения)
Пусть даны два положительных ряда
,(3.1) ,3.2)
и выполняются условия для всех n=1,2,…
Тогда: 1) из сходимости ряда (3.2) следует сходимость ряда (3.1);
2) из расходимости ряда (3.1) следует расходимость ряда (3.2).
Доказательство. 1. Пусть ряд (3.2) сходится и его сумма равна В. Последовательность частичных сумм ряда (3.1) является неубывающей ограниченной сверху числом В, т. е.
Определение сходящегося числового ряда- ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел, т. е.
В этом случае число называется суммой ряда и пишется
.
Признак Коши сходимости числового ряда с положительными членами. Исследовать на сходимость ряд-Предельный признак Коши
Пусть члены положительного ряда (1.1) таковы, что существует предел
 Тогда:
1) при q
< 1 ряд (1.1) сходится;
Тогда:
1) при q
< 1 ряд (1.1) сходится;
2) при q > 1 ряд (1.1) расходится;
3) при q = 1 о сходимости ряда (1.1) ничего сказать нельзя, необходимы дополнительные исследования
Пример 3.6. Исследовать на сходимость ряд
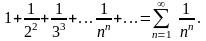
Применим предельный признак Коши:
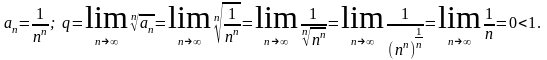
Следовательно, исходный ряд сходится.
33) Определение числового ряда с положительными членами- Такие ряды будем называть положительными рядами.
Теорема 3.1. (признак сравнения)
Пусть даны два положительных ряда
,(3.1) ,3.2)
и выполняются условия для всех n=1,2,…
Тогда: 1) из сходимости ряда (3.2) следует сходимость ряда (3.1);
2) из расходимости ряда (3.1) следует расходимость ряда (3.2).
Доказательство. 1. Пусть ряд (3.2) сходится и его сумма равна В. Последовательность частичных сумм ряда (3.1) является неубывающей ограниченной сверху числом В, т. е.
Определение сходящегося числового ряда-- ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел, т. е.
В этом случае число называется суммой ряда и пишется
.
Признак Коши сходимости числового ряда с положительными членами. Исследовать на сходимость ряд-Предельный признак Коши
Пусть члены положительного ряда (1.1) таковы, что существует предел
Тогда: 1) при q < 1 ряд (1.1) сходится;
2) при q > 1 ряд (1.1) расходится;
3) при q = 1 о сходимости ряда (1.1) ничего сказать нельзя, необходимы дополнительные исследования
Пример 3.6. Исследовать на сходимость ряд
Применим предельный признак Коши:
Следовательно, исходный ряд сходится.
признак сравнения)
Пусть даны два положительных ряда
, (3.1) , (3.2)
и выполняются условия для всех n=1,2,…
Тогда: 1) из сходимости ряда (3.2) следует сходимость ряда (3.1);
2) из расходимости ряда (3.1) следует расходимость ряда (3.2).
Доказательство. 1. Пусть ряд (3.2) сходится и его сумма равна В. Последовательность частичных сумм ряда (3.1) является неубывающей ограниченной сверху числом В, т. е.
Тогда в силу свойств таких последовательностей следует, что она имеет конечный предел, т. е. ряд (3.1) сходится.
2. Пусть ряд (3.1) расходится. Тогда, если ряд (3.2) сходится, то в силу доказанного выше пункта 1 сходился бы и исходный ряд, что противоречит нашему условию. Следовательно ряд (3.2) также расходится.
Этот признак удобно применять к определению сходимости рядов, сравнивая их с рядами, сходимость которых уже известна.
Пример 3.1. Исследовать на сходимость ряд

Члены ряда положительны и меньше соответствующих членов сходящегося ряда геометрической прогрессии
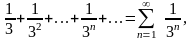 т.
к.
т.
к.
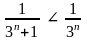 ,
n=1,2,…
,
n=1,2,…
Следовательно, по признаку сравнения исходный ряд также сходится.
Э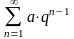 талонные
ряды-
талонные
ряды-
Геометрический ряд
с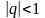
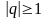 ходится
при
ходится
при
и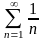 расходится при
расходится при
Г армонический
ряд
армонический
ряд
- расходится.
Обобщенный гармонический ряд
с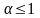
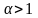 ходится
при
ходится
при
и расходится при
Исследовать на сходимость гармонический ряд

Применим интегральный признак Коши.
В
нашем случае функция
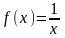 удовлетворяет условию теоремы(Интегральный
признак Коши)Исследуем
на сходимость несобственный интеграл
удовлетворяет условию теоремы(Интегральный
признак Коши)Исследуем
на сходимость несобственный интеграл
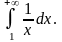
Имеем
 .
.
Несобственный интеграл расходится, следовательно, исходный гармонический ряд расходится также.
Пример 3.8. Исследовать на сходимость обобщенный гармонический ряд

Функция
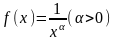 удовлетворяет условию теоремы 3.4.
удовлетворяет условию теоремы 3.4.
Исследуем
на сходимость несобственный интеграл

Рассмотрим следующие случаи:
1)
пусть
 Тогда обобщенный гармонический ряд
есть гармонический ряд, который
расходится, как показано в примере 3.7.
Тогда обобщенный гармонический ряд
есть гармонический ряд, который
расходится, как показано в примере 3.7.
2)
пусть
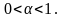 Тогда
Тогда
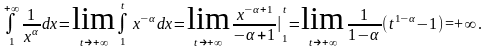
Несобственный интеграл расходится, и, следовательно, ряд расходится;
3)
пусть
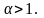 Тогда
Тогда

Несобственный интеграл сходится, и, следовательно, ряд сходится.
Окончательно имеем
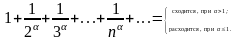
Замечания.
1. Обобщенный гармонический ряд будет
расходиться при
![]() ,
т. к. в этом случае не выполняется
необходимый признак сходимости: общий
член ряда не стремится к нулю.
,
т. к. в этом случае не выполняется
необходимый признак сходимости: общий
член ряда не стремится к нулю.
2. Обобщенный гармонический ряд удобно использовать при применении признака сравнения.
Пример 3.9. Исследовать на сходимость ряд
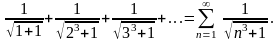
Члены ряда положительны и меньше соответствующих членов сходящегося обобщенного гармонического ряда
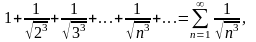
т.
к.
 и параметр
и параметр
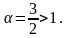
Следовательно, исходный ряд сходится (по признаку сравнения).
Перейдем к рассмотрению рядов, члены которых могут быть как положительными, так и отрицательными.
Тогда в силу свойств таких последовательностей следует, что она имеет конечный предел, т. е. ряд (3.1) сходится.

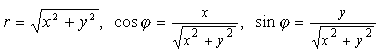 . (10)
. (10)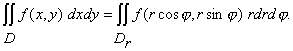 (11)
(11)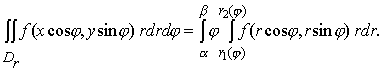 (12)
(12)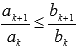 ,
то из сходимости ряда
следует сходимость
,
а из расходимости ряда
следует
расходимость
.
,
то из сходимости ряда
следует сходимость
,
а из расходимости ряда
следует
расходимость
.