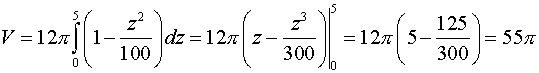Площадь криволинейной трапеции.

Рассмотрим криволинейную трапецию – фигуру, ограниченную сверху и снизу графиками непрерывных функций , а с боков вертикальными прямыми:

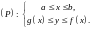
Утверждение. Описанная выше фигура квадрируема, а ее площадь равна

.

Пример 3. Найти площадь области, ограниченной кривым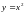и и .

Решение: .

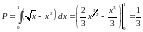17. Интеграл по симметричному промежутку для четной и нечетной функции

Несобственный  интеграл  на интервале (-∞ , +∞) определяется следующим образом:

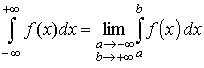
 Если  функция  f(x)  нечётная , то  интеграл   по   симметричному   промежутку  (- а, + а) равен нулю,  и  поэтому для  нечётной   функции :

.

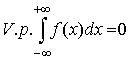   Если  функция  f(x)  чётная , то  интеграл   по   симметричному   промежутку  (- а, + а) равен удвоенному значению  интеграла  по половине  промежутка интегрирования,  и  поэтому  для   чётной   функции :

.

Например,

.

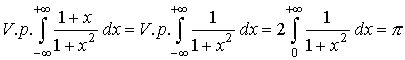18. Вычисление площадей фигур с помощью определенного интеграла. Вывод формулы.

Площадь плоской фигуры, ограниченной областью D, находится по формуле

. (1)

Если область определена  в прямоугольной системе координат неравенством  , то из (1) имеем

.

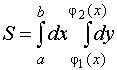Если область D определена в полярных координатах неравенством 

,  , то

.

Если гладкая однозначная поверхность задана уравнением z = f (x,y),

То площадь этой поверхности выражается формулой: ,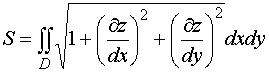

где D есть проекция данной поверхности на плоскость хОу.

Если поверхность задана уравнением x = f (y, z),

то для вычисления площади имеем аналогичную формулу:

.

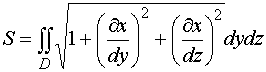Однако здесь D есть проекция поверхности на плоскость yOz.

Аналогично, если поверхность задана уравнением  y = f (x, z),

,

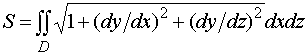где D – проекция поверхности на плоскость xOz.

Пример : Найти площадь области, ограниченной кривым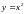и и .

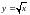Решение: .

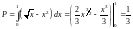19. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Вывод формулы.

Пусть известна функция   и требуется найти  длину   дуги , заданной функцией   , где   .

Для определения  длины   дуги    необходимо вычислить  определенный   интеграл :

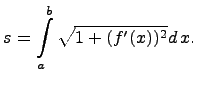
Рассмотрим случай параметрического задания  кривой :

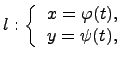
где   . В этом случае для определения  длина   дуги    вычисляется  определенный  интеграл :

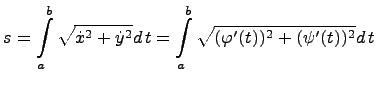
Рассмотрим случай, когда  кривая  задается в полярных координатах   где  . Тогда для определения  длины   дуги    вычисляется следующий  определенный  интеграл :

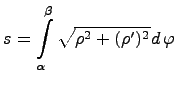
Пример : Найти длину дуги кривой от до .

Решение: .

20. Вычисление объема тела по площади поперечного сечения. Объем тела вращения. Вывод формулы.

Вычисление   объема   тела  по известным  площадям   поперечных   сечений .

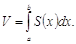
Если  площадь   сечения   тела  плоскостью, перпендикулярной оси Ox, может быть выражена как функция от x, т.е. в виде  , то  объем  части тела , заключенной между перпендикулярными оси Ox плоскостями x=a и x=b, находится по  формуле 

 Вычисление   объема   тела   вращения . Если криволинейная трапеция, ограниченная кривой   и прямыми   вращается вокруг оси Ox, то  объем  тела   вращения  вычисляется по  формуле 

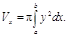
Если фигура, ограниченная кривыми  и прямыми x=a, x=b, вращается вокруг оси Ox, то  объем   тела   вращения 

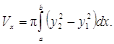
План решения.

Если   - площадь сечения тела плоскостью, перпендикулярной к оси   и пересекающей ее в точке с абсциссой  , то объем  части тела, заключенной между плоскостями   и  , определяется формулой .      (1)

1. Находим  .

2. Находим объем согласно формуле(1).

Задача 20. Вычислить объемы тел, ограниченных поверхностями.

.

Сделаем чертеж.

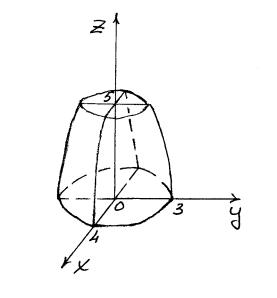
Поперечным сечением является эллипс:

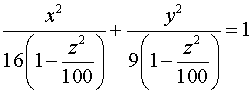
Площадь  эллипса:

Объем: