Необходимое и достаточное условие интегрируемости

   Для того чтобы ограниченная на отрезке [a, b] функция f (x) была интегрируемой на этом отрезке, необходимо и достаточно, чтобы  .    Это условие означает, что для любого как угодно малого ε > 0 существует δ = δ (ε) > 0 такое, что при λ < δ выполняется неравенство |S - s| < ε. Так как s ≤ S, то последнее неравенство равносильно неравенству S - s < ε.    Доказательство. (Необходимость) Пусть функция f (x) интегрируема на отрезке [a, b], т. е. существует определенный интеграл 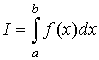 . Это означает, что для любого как угодно малого ε > 0 существует δ = δ (ε) > 0 такое, что для любого разбиения τ, удовлетворяющего условию λ < δ, независимо от выбора точек ξ _i выполняется неравенство

.

Зафиксируем любое такое разбиение τ. Для него можно указать такие интегральные суммы σ',σ'', что

.

Отметим, что обе интегральные суммы σ',σ''  удовлетворяют неравенству |σ - I| < ε / 4. Из соотношения следует, что S - s < ε.    Достаточность. Пусть выполнено условие S - s < ε. Предположим, что интеграл зависит от способа разбиения и существует два его значения I^* и I_*. Согласно свойству s ≤ I_* ≤ I^* ≤ S для любых нижних и верхних сумм Дарбу, поэтому 0 ≤ I^* - I_* ≤ S - s, откуда следует, что 0 ≤ I^* - I_* < ε для любого ε > 0. Значит, I^*- I_*= 0, т. е. I^* = I_*. Полагая I = I^* = I_*, получаем, что для любого разбиения выполняются неравенства s ≤ I ≤ S. Если же интегральная сумма σ и суммы Дарбу s и S отвечают одному и тому же разбиению τ то, как известно, s ≤ σ ≤ S. Из вышесказанного следует, что | σ - I | ≤ S - s. По условию для любого ε > 0 существует δ > 0 такое, что при λ < δ выполняется неравенство S - s < ε. Но тогда имеем, что | σ - I | < ε  при λ < δ, а это означает, что число I является пределом интегральной суммы σ при λ → 0, т. е. функция f (x) интегрируема на отрезке [a, b]. В дальнейшем понадобится другая форма записи необходимого и достаточного условия интегрируемости. Обозначая колебанием M _i - m_i функции f (x) на отрезке [x_{i - 1}, x_i] через ω _i, имеем

.

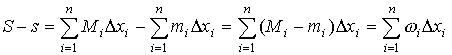Так как M _i ≥ m _i и Δ х_i > 0, то каждое слагаемое в последней сумме неотрицательно, и условие существования определенного интеграла можно переписать так: для любого как угодно малого ε > 0 существует ε = δ (ε) > 0 такое, что 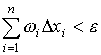  при λ < δ.

Интегрируемость непрерывных функций

   Если функция f (x) непрерывна на отрезке [a, b], то она интегрируема на нем.    Доказательство. Так как функция f (x) непрерывна на отрезке [a, b], то по теореме Кантора она равномерно непрерывна на нем. Выберем произвольное как угодно малое ε > 0. Согласно следствию из теоремы Кантора для положительного числа ε /(b - a) найдется δ > 0 такое, что при разбиении отрезка [a, b] на частичные отрезки [x _{i - 1}, x_i], длина которых Δ x_i < δ, все колебания ω_i меньше ε /(b - a). Отсюда

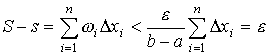 при λ < δ.

   Следовательно, для непрерывной на отрезке [a, b] функции f (x) выполнено достаточное условие интегрируемости, а из него вытекает существование определенного интеграла.

Определение и свойства определенного интеграла

Пусть y=f(x) непрерывна на [a;b], разобьём отрезок произвольно на n-частей a=x0<x1<x2<…<xn=b В каждом частичном отрезке возьмем произвольным образом точку ξi, найдем значение функции f(ξi) в т. ξi и составим сумму

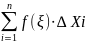(1)

где 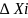=X_i-X_i-1 ; (1) называется интегральной суммой функции y=f(x) на отр-ке [a;b].

Опр.1 Если существует конечный предел интегральной суммы (1) при d=max , независящей от способа разбиения отрезка [a;b], ни от способа выбора точек ξi, то этот предел называется определенным интегралом ф-ции на [a;b].

Обозн.

a-нижний предел интегр., b – верхний

Теорема 1 (необходимое условие интегрирования)

Если ф-ция y=f(x) интегрируема на отрезке [a;b], т.е. Ǝ конечный предел интегральной суммы (1), то функция y=f(x) ограничена на этом отрезке.

Обратное утверждение неверно, т.е. Ǝ ограниченные функции на отрезке, которые не являются интегрируемыми.

Пример:

Теорема 2 (достаточные условия существования определенного интеграла)

Функция y=f(x) интегрируема на отрезке [a;b], если выполняется одно из следующих условий:

1. y=f(x) непрерывна на [a;b]

2. y=f(x) монотонна и ограничена на [a;b]

3. y=f(x) имеет конечное число точек разрыва Iго рода (пределы разные, но конечные)