
- •Основные радиотехнические процессы
- •Классификация цепей
- •Классификация сигналов
- •Характеристики детерминированных сигналов
- •Гармонический анализ периодических сигналов
- •Примеры спектров периодических сигналов
- •Распределение мощности в спектре периодического сигнала.
- •Гармонический анализ непериодических сигналов
- •Свойства преобразования Фурье
- •Примеры спектров непериодических сигналов
- •Распределение энергии в спектре непериодического сигнала
- •Соотношение между длительностью сигнала и широтой его спектра
- •Скорость убывания спектра вне основной полосы
- •Модуляция
- •Угловая модуляция.
- •Спектр колебания при угловой модуляции.
- •Спектр колебания при амплитудно-частотной модуляции
- •Узкополосный сигнал
- •Аналитический сигнал
- •Частотные и временные характеристики радиотехнических цепей
- •Апериодический усилитель
- •Резонансный усилитель
- •Обратная связь усилителя
- •Дифференцирующая и интегрирующая цепи
- •Спектральный метод.
- •Операторный метод
- •Метод интеграла наложения.
- •Метод огибающей.
- •Прохождение импульсного сигнала через дифференцирующие и интегрирующие цепи
- •Прохождение радиоимпульса через резонансный усилитель.
- •Прохождение ам – колебаний через резонансный усилитель.
- •Прохождение частотно – модулированного колебания через избирательные цепи.
- •Прохождение фазоманипулированного колебания через резонансную цепь.
Спектр колебания при амплитудно-частотной модуляции
Пусть амплитуда задана функцией A(t):

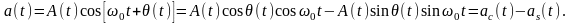
Определение спектра
колебания сводится к нахождению спектров
функций
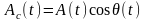 и
и
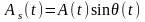 ,
т. е. огибающих
квадратурных колебаний, и к последующему
сдвигу этих спектров на величину ω0.
,
т. е. огибающих
квадратурных колебаний, и к последующему
сдвигу этих спектров на величину ω0.
Обозначим
спектральные плотности функций
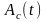 и
и
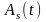 символами
символами
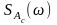 и
и
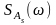 .
Тогда:
.
Тогда:
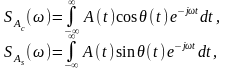
Спектральная
плотность косинусного квадратурного
колебания
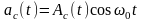 при
при
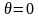 будет
будет
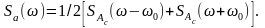
При определении
спектра синусного квадратурного
колебания
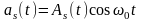 фазовый,
угол
фазовый,
угол
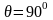 .
Следовательно,
.
Следовательно,
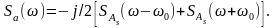 .
.
В области положительных частот можно считать
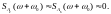
Таким образом,
окончательно спектральная плотность
колебания
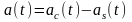 определяется выражением
определяется выражением
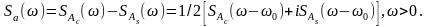
Переходя к переменной
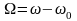 ,
получаем:
,
получаем:
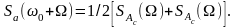
Структура спектра колебания а(t) при амплитудно-частотной модуляции зависит от соотношения и вида функций A(t) и θ(t).
При АМ спектр
колебания а(t)
характеризуется
полной симметрией амплитуд и фаз
колебаний боковых частот относительно
несущего колебания; при угловой модуляции
фазы колебаний нижних боковых частот
при нечетных п
сдвинуты на
180°. Одновременная модуляция по амплитуде
и углу может при некоторых соотношениях
между A(t)
и θ(t)
приводить
к асимметрии спектра
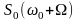 относительно ω0
не только по фазам, но и по амплитудам.
В частности, если θ(t)
является
нечетной функцией t,
то при любой
функции A(t)
спектр
колебания а
(t)
несимметричен.
относительно ω0
не только по фазам, но и по амплитудам.
В частности, если θ(t)
является
нечетной функцией t,
то при любой
функции A(t)
спектр
колебания а
(t)
несимметричен.
П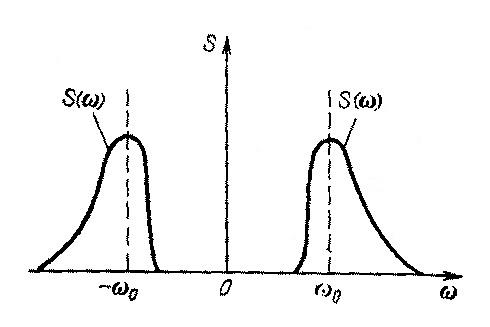 ример
подобного спектра представлен на
рисунке. (По отношению к точке ω
= 0 модуль
спектральной плотности симметричен
при любых условиях.)
ример
подобного спектра представлен на
рисунке. (По отношению к точке ω
= 0 модуль
спектральной плотности симметричен
при любых условиях.)
Для симметрии
спектра
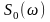 требуется четность функции θ(t)
при одновременном условии, чтобы функция
A(t)
была либо четной, либо нечетной функцией
t.
Если функция A(t)
может быть
представлена в виде суммы четной и
нечетной составляющих, то спектр
несимметричен даже при четной функции
θ(t).
требуется четность функции θ(t)
при одновременном условии, чтобы функция
A(t)
была либо четной, либо нечетной функцией
t.
Если функция A(t)
может быть
представлена в виде суммы четной и
нечетной составляющих, то спектр
несимметричен даже при четной функции
θ(t).
Наглядное представление о деформации спектра колебания при смешанной модуляции — амплитудной и угловой — можно получить, рассмотрев случай, когда обе модуляции осуществляются гармонической функцией с одной и той же частотой Ω. Для упрощения анализа зададим эту функцию в виде гармонического колебания cosΩt для угловой модуляции и в виде cosΩt или sinΩt для амплитудной.
Р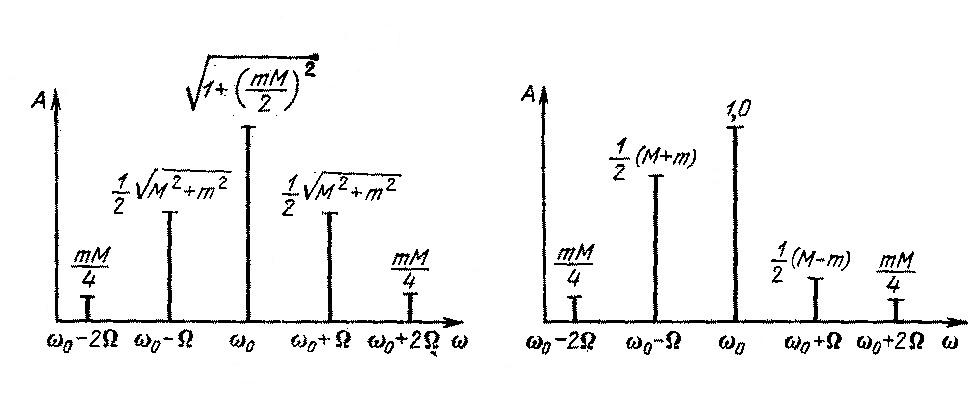 исунок
иллюстрирует спектр колебания при
одновременной модуляции амплитуды и
частоты гармонической функцией
исунок
иллюстрирует спектр колебания при
одновременной модуляции амплитуды и
частоты гармонической функцией
Рис.а рис.б
1. Обе функции, как А(t), так и Ω(t), четные относительно t:
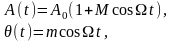
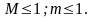
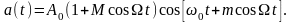
Приводим это выражение к виду:
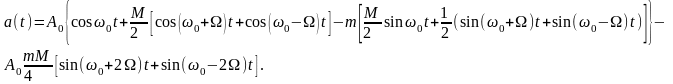
Суммируя квадратурные
составляющие
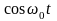 и
и
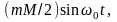 получаем
для амплитуды результирующего колебания
на частоте ω0
следующее выражение:
получаем
для амплитуды результирующего колебания
на частоте ω0
следующее выражение:
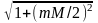 при A0
= 1. Аналогичным образом находим амплитуду
0,5
при A0
= 1. Аналогичным образом находим амплитуду
0,5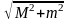 для колебаний с частотами ω0+Ω
и тМ/4 для
частот ω0±2Ω.
Спектр колебания для рассматриваемого
случая, представленный на рис.а,
симметричен.
для колебаний с частотами ω0+Ω
и тМ/4 для
частот ω0±2Ω.
Спектр колебания для рассматриваемого
случая, представленный на рис.а,
симметричен.
2. Функция Ω(t) — четная, а A(t) содержит четную и нечетную составляющие:
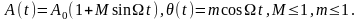
Выкладки, аналогичные предыдущим, приводят к следующим результатам: амплитуда равна 1 на частоте ω0; 1/2(М—т) на частоте ω0—Ω; 1/2(М +m) на частоте ω0—Ω; тМ/4 на частотах ω0±2Ω. Спектр колебания для рассматриваемого случая представлен на рис.б. Симметрия спектра нарушается в данном примере из-за неодинаковых амплитуд колебаний верхней и нижней боковых частот.
Асимметрия спектра при амплитудно-угловой модуляции может рассматриваться как показатель неправильной работы устройства, осуществляющего АМ; перекос спектра указывает на то, что полезная АМ сопровождается паразитной угловой модуляцией.
40, 41
ЛЧМ – сигнал и его спектр.
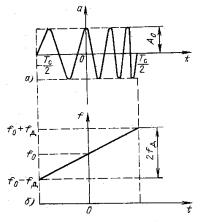
При модуляции частоты колебания по закону, отличающемуся от гармонического, нахождение спектра колебания усложняется. Выбор наиболее удобного метода анализа зависит от характера модулирующей функции. Поясним один из возможных методов на примере широко распространенного сигнала — импульса с линейной частотной модуляцией (ЛЧМ импульса). Подобный сигнал изображен на рисунке сверху, а закон изменения частоты заполнения импульса — на рисунке снизу.
Мгновенную частоту
заполнения
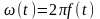 можно определить выражением
можно определить выражением
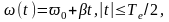
где
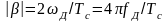 - скорость линейного изменения частоты
внутри импульса. Тогда мгновенное
значение колебания, представленного
на рис. а,
можно
записать в виде
- скорость линейного изменения частоты
внутри импульса. Тогда мгновенное
значение колебания, представленного
на рис. а,
можно
записать в виде
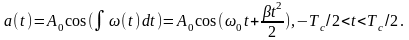
Произведение
полной девиации частоты на
длительность импульса
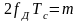 является основным параметром ЛЧМ
сигнала. Это так называемая база сигнала.
С учетом выкладок, выражение можно
записать в форме:
является основным параметром ЛЧМ
сигнала. Это так называемая база сигнала.
С учетом выкладок, выражение можно
записать в форме:
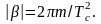
При этом сигнал
а (t)
определяется
при β> 0 выражением
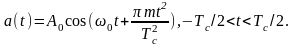
Определим спектральную плотность этого сигнала с помощью общего выражения:
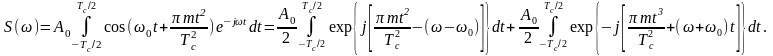
Первое слагаемое
в правой части полученного выражения
определяет всплеск спектральной
плотности вблизи частоты
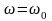 ,
а второе — всплеск вблизи частоты
.
,
а второе — всплеск вблизи частоты
.
При определении
S(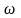 )
в области положительных частот второе
слагаемое можно отбросить. В первом
же слагаемом показатель степени в
подынтегральной функции целесообразно
дополнить до квадрата разности (β
считаем положительной величиной)
)
в области положительных частот второе
слагаемое можно отбросить. В первом
же слагаемом показатель степени в
подынтегральной функции целесообразно
дополнить до квадрата разности (β
считаем положительной величиной)
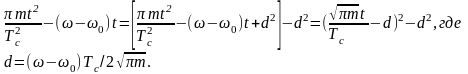
Переходя к новой
переменной
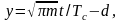 получаем:
получаем:
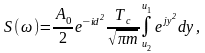
г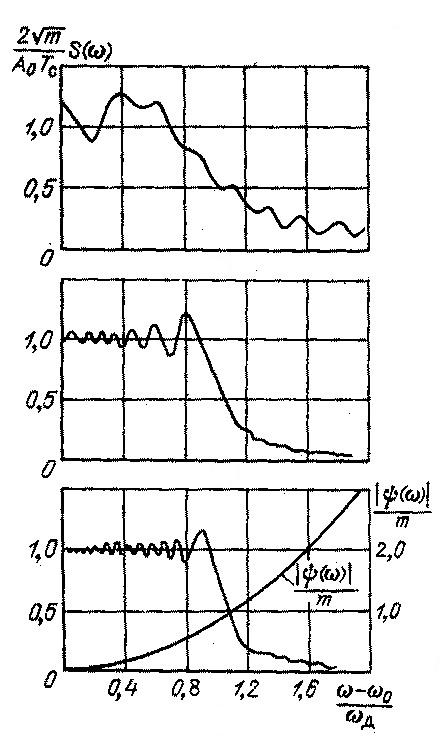 де
пределы интегрирования определяются
выражениями:
де
пределы интегрирования определяются
выражениями:
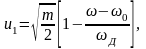
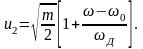
Используем известные из математики определения интегралов Френеля
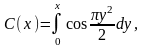
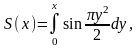 откуда
откуда

В области
положительной частоты имеем АЧХ:
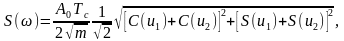
А ФЧХ: .
.
Из графиков видно,
что при увеличении m
форма S(
)
стремится к прямоугольной, а ШС = 2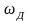 ,
при этом
,
при этом
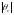 принимает квадратичный вид (второе
слагаемое в
принимает квадратичный вид (второе
слагаемое в
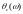 стремящееся к
стремящееся к
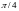 опускается).
опускается).
При
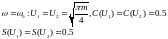 ,
,
Вследствие чего
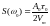 .
.
В области
отрицательных частот ФЧХ ЛЧМ сигнала
противоположны по знаку. При
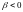 ,
то есть при уменьшении с течением времени
частоты заполнения в радиоимпульсе
перед правой частью выражение для
знак изменяется на обратный.
,
то есть при уменьшении с течением времени
частоты заполнения в радиоимпульсе
перед правой частью выражение для
знак изменяется на обратный.
42, 43
