Примеры спектров непериодических сигналов

Прямоугольный импульс

Определяется выражением

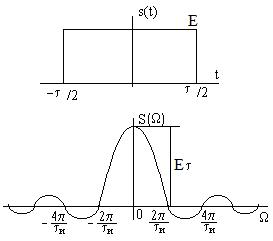
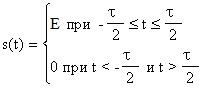
Найдем спектральную плотность

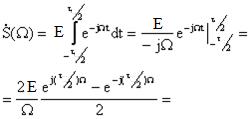
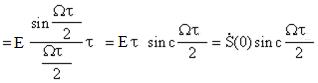
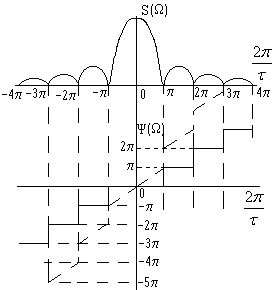
При удлинении (растягивании) импульса расстояние между нулями сокращается, значение S(0) при этом увеличивается. Модуль функции можно рассматривать как АЧХ, а аргумент как ФЧХ спектра прямоугольного импульса. Каждая перемена знака учитывает приращение фазы на p.

При отсчете времени не от середины импульса, а от фронта ФЧХ спектра импульса должна быть дополнена слагаемым 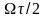, учитывающим сдвиг импульса на время 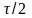 (результирующая ФЧХ показана пунктиром). , .

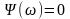Треугольный импульс

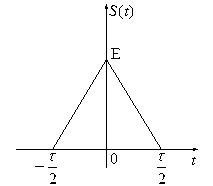
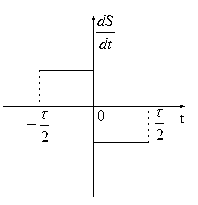
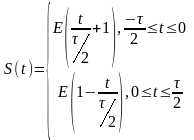
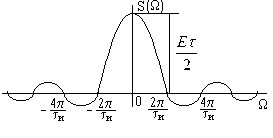
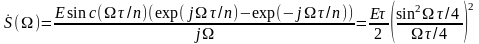. Уровень боковых лепестков убывает пропорционально 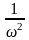, а не , как у прямоугольного импульса.

Колоколообразный (гауссовский) импульс

Определяется выражением

.

Постоянная а имеет смысл половины длительности импульса, определяемой на уровне е^-1/2 от амплитуды импульса. Таким образом, полная длительность импульса .

Спектральная плотность сигнала

.

Для удобства дополним показатель степени до квадрата суммы

,

где величина d определяется из условия , откуда

.

Таким образом, выражение для спектральной плотности можно привести к виду

.

Переходя к новой переменной  получим

  .

Учитывая, что входящий в это выражение интеграл равен , окончательно получим

,

где .

Ширина спектра импульса .

Гауссовский импульс и его спектр выражаются одинаковыми функциями и обладают свойством симметрии. Для него соотношение длительности импульса и полосы пропускания является оптимальным, т. е. при данной длительности импульса гауссовский импульс имеет минимальную полосу пропускания.

Импульс вида sinc(x)

.

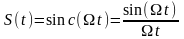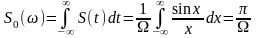
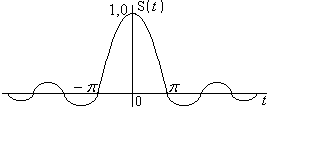
Пачка импульсов

.

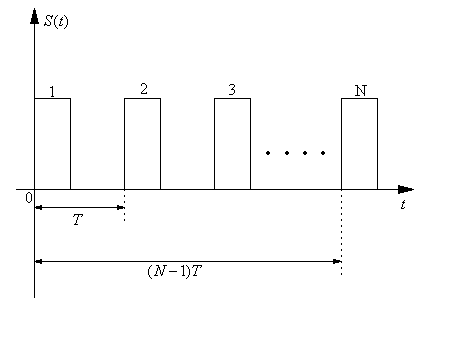
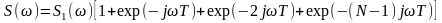При 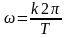, где 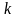– целое число 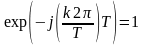и 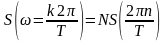, то есть модуль спектральной плотности пачки импульсов в точке 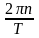в N раз больше модуля спектра одиночного импульса.

При , .

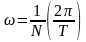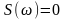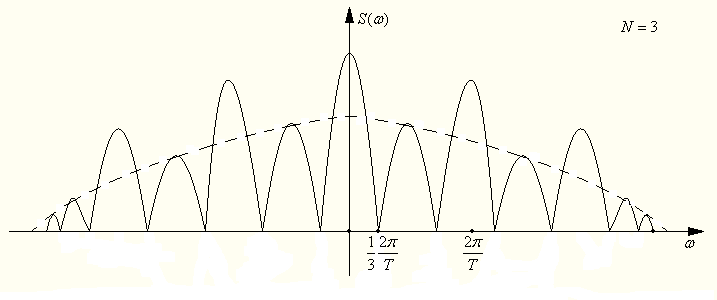
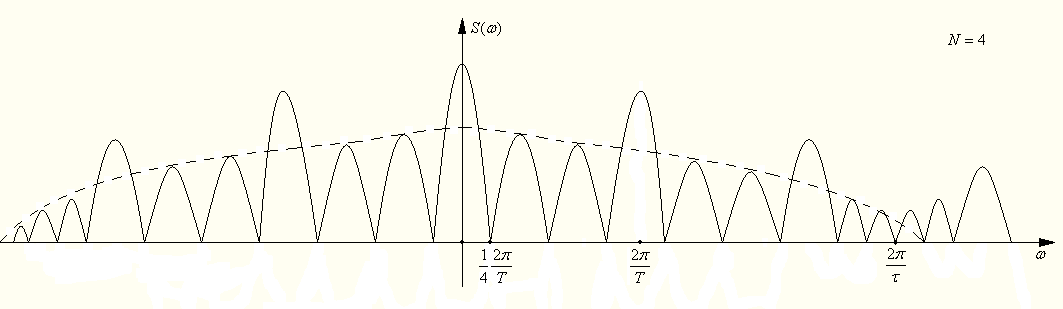
При увеличении N спектр расширяется и при принимает линейную структуру периодической функции.

Дельта-импульс (единичный импульс)

Ниже приведены возможные импульсы, площадь которых равна едини­це:

Импульсы, обращающиеся в дельта-функцию при стремлении длительности к нулю.

Амплитуды всех этих импульсов обратно про­порциональны соответствующим образом определенной длительности импульса. При стремлении длительности к нулю амплитуда обращается в бесконечность, а площадь импульса остается неизменной и равной единице.

Сигнал задан соотношением

  .

Ее можно получить из вышеперечисленных импульсов путем устремления t_и к нулю.

, следовательно спектр такого сигнала будет постоянным (это есть площадь импульса равна единице).

- стробирующее свойство дельта-функции.

Так как по определению функция 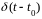равна нулю на всей оси t, кроме точки t =t₀ (где она бесконечно велика), то промежуток интегриро­вания можно сделать сколь угодно малым, лишь бы он включал в себя точ­ку х₀. В этом промежутке функции 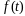принимает постоянное значение 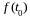, которое можно вынести за знак интеграла. Таким образом, умноже­ние любой подынтегральной функции на позволяет прирав­нять интеграл произведения значению в точке t =t₀

В теории сигналов приходится иметь дело с дельта-функциями от аргу­ментов t или ω, в зависимости от того, в какой области рассматривается функция — во временной или частотной.

Рассмотрим сначала свойства функции 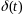. В этом случае основное значение имеет спектральная характеристика дельта-функции. Ранее было установлено, что при сокращении длительности прямоугольного импульса (неизменной амплитуды) ширина основного лепестка спектраль­ной плотности увеличивается, а величина S(0) быстро уменьшается. В дан­ном же случае, когда уменьшение длительности импульса сопровождается одновременным увеличением его амплитуды, значение спектральной плот­ности остается неизменным и равным величине S(0) = 1 для всех частот. То же самое имеет место при укорочении любого из импульсов.

Следовательно, спектральная плотность дельта-функции вещественна и равна единице для всех частот. Из этого также вытекает, что ФЧХ спектра дельта-функции равна нулю для всех частот. Это означает, что все гармонические составляющие единичного импульса при нулевых начальных фазах, суммируясь, образуют пик бесконечно большой величины в момент времени t = 0.

Аналогично функция , определяющая единичный импульс в момент t₀, имеет спектральную плотность 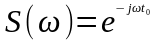. Модуль этой функ­ции по-прежнему равен единице, а ФЧХ .

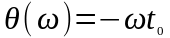Найденная ранее спектральная плотность дельта-функции может быть получена и с помощью преобразования Фурье:

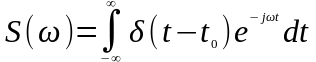
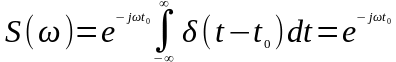
При t₀ = 0 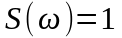. Следует иметь в виду, что правая часть равенства является размерной единицей: это площадь импульса, численно-равная единице. Если под подразумевается импульс напряжения, то размерность 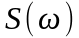есть вольт на секунда (В*с).

Для создания такого импульса необходимы все гармоники.

Экспоненциальный импульс

Сигнал вида , c>0.

Спектр сигнала находится следующим образом

Запишем сигнал в другой форме

.

Если c>0, то . Это означает, что мы получим единичный скачек. При

получаем следующее выражение для спектра сигнала

.

Отсюда модуль ,

а фаза

Гармонический сигнал

.

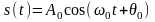
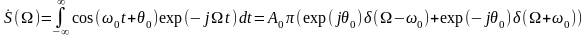При 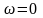– постоянное напряжение:

.

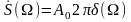Если , .

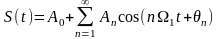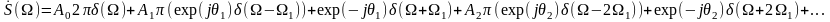Если 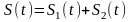, то:

14