
- •Основные радиотехнические процессы
- •Классификация цепей
- •Классификация сигналов
- •Характеристики детерминированных сигналов
- •Гармонический анализ периодических сигналов
- •Примеры спектров периодических сигналов
- •Распределение мощности в спектре периодического сигнала.
- •Гармонический анализ непериодических сигналов
- •Свойства преобразования Фурье
- •Примеры спектров непериодических сигналов
- •Распределение энергии в спектре непериодического сигнала
- •Соотношение между длительностью сигнала и широтой его спектра
- •Скорость убывания спектра вне основной полосы
- •Модуляция
- •Угловая модуляция.
- •Спектр колебания при угловой модуляции.
- •Спектр колебания при амплитудно-частотной модуляции
- •Узкополосный сигнал
- •Аналитический сигнал
- •Частотные и временные характеристики радиотехнических цепей
- •Апериодический усилитель
- •Резонансный усилитель
- •Обратная связь усилителя
- •Дифференцирующая и интегрирующая цепи
- •Спектральный метод.
- •Операторный метод
- •Метод интеграла наложения.
- •Метод огибающей.
- •Прохождение импульсного сигнала через дифференцирующие и интегрирующие цепи
- •Прохождение радиоимпульса через резонансный усилитель.
- •Прохождение ам – колебаний через резонансный усилитель.
- •Прохождение частотно – модулированного колебания через избирательные цепи.
- •Прохождение фазоманипулированного колебания через резонансную цепь.
Спектр колебания при угловой модуляции.
Пусть задано колебание
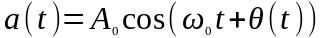 ,
о котором известно, что передаваемое
сообщение
,
о котором известно, что передаваемое
сообщение
 заложено в функцию
заложено в функцию
 .
Если колебание
получено с помощью ФМ, то
и
полностью совпадают по форме и отличаются
лишь постоянным коэффициентом. При этом
очевидно, с точностью до постоянного
коэффициента совпадают и спектры
функций
и
.
Если колебание
получено с помощью ФМ, то
и
полностью совпадают по форме и отличаются
лишь постоянным коэффициентом. При этом
очевидно, с точностью до постоянного
коэффициента совпадают и спектры
функций
и
При ЧМ функция является интегралом от передаваемого сообщения . Так как интегрирование является линейным преобразованием, то при ЧМ спектр функции состоит из тех же компонентов, что и спектр сообщения , но с измененными амплитудами и фазами.
Отвлекаясь от способа осуществления угловой модуляции — фазовой или частотной — и считая заданным спектр функции , находим спектр модулированного колебания . Для этого выражение преобразуем к виду:
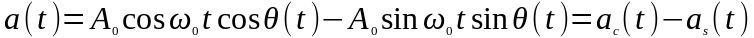
Отсюда следует,
что модулированное по углу колебание
можно рассматривать как сумму двух
квадратурных
колебаний:
косинусного
 и
синусного
и
синусного
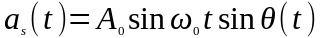 каждое из
которых модулировано только по амплитуде;
закон АМ для косинусного колебания
определяется медленной функцией
каждое из
которых модулировано только по амплитуде;
закон АМ для косинусного колебания
определяется медленной функцией
 ,
а синусного
— функцией
,
а синусного
— функцией
 .
.
Ранее было установлено, что для определения спектра амплитудно-модулированного колебания достаточно сдвинуть на частоту спектр огибающей амплитуд. Следовательно, для нахождения спектра колебания , необходимо сначала найти спектры функций и , т. е. спектры огибающих квадратурных колебаний. Перенос этих спектров на частоту можно затем осуществить таким же образом, как и при обычной АМ.
Из приведенных рассуждений следует, что при одном и том же передаваемом сообщении спектр колебания, модулированного по углу, значительно сложнее, чем спектр модулированного по амплитуде. Действительно, так как и являются нелинейными функциями своего аргумента , то спектры этих функций могут существенно отличаться от спектра функции ; возможно возникновение кратных и комбинационных частот, как это имеет место при обычных нелинейных преобразованиях спектра.
Это обстоятельство, а также наличие двух квадратурных слагаемых показывают, что при угловой модуляции спектр модулированного колебания нельзя получить простым сдвигом спектра сообщения на величину несущей частоты , как это имеет место при АМ. При угловой модуляции связь между спектрами сообщения и модулированного колебания оказывается более сложной.
При тональной модуляции
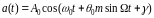 .
.
Это совпадает с
ЧМ при
![]() Если
Если
![]() ,
,
![]() ,
то получаем:
,
то получаем:
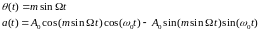
Разложим периодические
функции
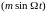 и
и
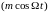 в ряд Фурье, получим:
в ряд Фурье, получим:
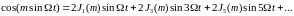 ,
,
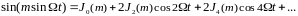 ,
,
где
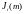 - Бесселева функция первого рода, i-ого
порядка от аргумента m.
При подстановки в вышеприведенное
выражение конкретной функции получим:
- Бесселева функция первого рода, i-ого
порядка от аргумента m.
При подстановки в вышеприведенное
выражение конкретной функции получим:
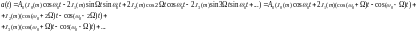
То есть при ЧМ и
ФМ спектр состоит из бесконечных чисел
боковых частот попарно расположенных
относительно
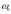 и отличающихся на
и отличающихся на
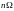 .
Амплитуда n-ой
боковой составляющей
.
Амплитуда n-ой
боковой составляющей
 ,
то есть вклад боковых частот в суммарную
мощность модулированных колебаний
определяется величиной m.
,
то есть вклад боковых частот в суммарную
мощность модулированных колебаний
определяется величиной m.
Если m<<1,
то
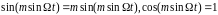 .
Тогда:
.
Тогда:
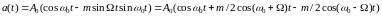 .
.
Сравнивая с АМ колебанием:
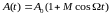 и
и
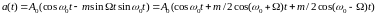 .
.
Боковая несущая
частота
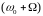 противоположна по фазе другой боковой
частоте при УМ.
противоположна по фазе другой боковой
частоте при УМ.
При
 ширина спектра равна
ширина спектра равна
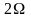 .
.
Если m=0.5-1, то в спектре возникает вторая пара боковых частот и ширина спектра =4Ω.
Если же m>>1,
то
 равномерна при всех целых
равномерна при всех целых
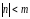 .
При
.
При
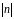 близких к m,
то
близких к m,
то
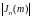 образует всплеск, а при увеличении m
убывает до нуля.
образует всплеск, а при увеличении m
убывает до нуля.
В этом случае ширина спектра:
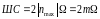 ,
где
,
где
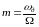 ,
то есть
,
то есть
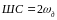 .
.
Модуляция с m<<1
называется быстрой модуляцией (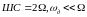 )
)
Модуляция с m>>1
называется медленной модуляцией (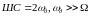 )
)
??
