
- •Основные радиотехнические процессы
- •Классификация цепей
- •Классификация сигналов
- •Характеристики детерминированных сигналов
- •Гармонический анализ периодических сигналов
- •Примеры спектров периодических сигналов
- •Распределение мощности в спектре периодического сигнала.
- •Гармонический анализ непериодических сигналов
- •Свойства преобразования Фурье
- •Примеры спектров непериодических сигналов
- •Распределение энергии в спектре непериодического сигнала
- •Соотношение между длительностью сигнала и широтой его спектра
- •Скорость убывания спектра вне основной полосы
- •Модуляция
- •Угловая модуляция.
- •Спектр колебания при угловой модуляции.
- •Спектр колебания при амплитудно-частотной модуляции
- •Узкополосный сигнал
- •Аналитический сигнал
- •Частотные и временные характеристики радиотехнических цепей
- •Апериодический усилитель
- •Резонансный усилитель
- •Обратная связь усилителя
- •Дифференцирующая и интегрирующая цепи
- •Спектральный метод.
- •Операторный метод
- •Метод интеграла наложения.
- •Метод огибающей.
- •Прохождение импульсного сигнала через дифференцирующие и интегрирующие цепи
- •Прохождение радиоимпульса через резонансный усилитель.
- •Прохождение ам – колебаний через резонансный усилитель.
- •Прохождение частотно – модулированного колебания через избирательные цепи.
- •Прохождение фазоманипулированного колебания через резонансную цепь.
Метод огибающей.
В рассмотренных в предыдущей главе задачах мы имели дело с сигналами, которые по своей форме совпадали с формой передаваемого сообщения. При передаче подобных сообщений задача сохранения информации тесно связана с задачей сохранения формы сигналов.
Иначе обстоит дело с радиосигналом, в котором информация заключена водном из нескольких параметров высокочастотного колебания. Не обязательно сохранять полностью структуру этого колебания; достаточно лишь сохранить закон изменения того параметра, в котором заключена информация. Так, в случае амплитудно-модулированного колебания важно точно передать огибающую амплитуд, между тем как некоторое изменение частоты или фазы заполнения, не имеющее существенного значения, при анализе можно не учитывать. При передаче радиосигналов с угловой модуляцией, наоборот, основное внимание следует уделить точному воспроизведению закона изменения частоты и фазы.
Эти особенности радиосигналов открывают путь к упрощению методов анализа передачи их через линейные цепи. Возможность упрощения особенно существенна, когда радиосигнал представляет собой узкополосный процесс, а цепь — узкополосную систему. Это как раз и характерно для реальных радиосигналов и реальных избирательных цепей. Ранее отмечалось, что даже для «широкополосных» сигналов ширина спектра радиосигнала мала по сравнению с несущей частотой сигнала. Соответственно и полоса прозрачности цепи обычно мала по сравнению с ее резонансной частотой.
Анализ передачи сигнала в подобной ситуации существенно упрощается при использовании понятия аналитического сигнала:
 ,
,
где комплексная огибающая A(t) содержит всю информацию, заложенную в сигнал в результате модуляции, как амплитудной, так и угловой.
После прохождения через заданную цепь получается новый аналитический сигнал:
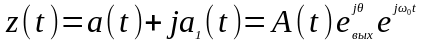 ,
действительная часть которого:
,
действительная часть которого:
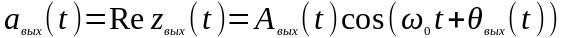 и есть выходной
сигнал.
и есть выходной
сигнал.
Таким образом, задача сводится к определению влияния цепи на комплексную огибающую входного сигнала.
Эта задача может быть решена двумя способами: спектральным и временным.
1) Спектральный метод.
Спектральная
плотность высокочастотного модулированного
колебания образует два всплеска
вблизи частот
и
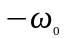 ,
а передаточная функция
— вблизи частот
и
.
Для общности здесь принято, что резонансная
частота может не совпадать с центральной
частотой сигнала
,
т. е. может иметь место расстройка. При
этом предполагается, что расстройка
является величиной того же порядка, что
и полоса прозрачности цепи. Спектральная
плотность сигнала
,
а передаточная функция
— вблизи частот
и
.
Для общности здесь принято, что резонансная
частота может не совпадать с центральной
частотой сигнала
,
т. е. может иметь место расстройка. При
этом предполагается, что расстройка
является величиной того же порядка, что
и полоса прозрачности цепи. Спектральная
плотность сигнала
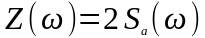 отлична от нуля только в области
положительных частот. Очевидно, что:
отлична от нуля только в области
положительных частот. Очевидно, что:
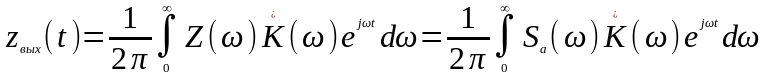
 - спектральная
плотность огибающей.
- спектральная
плотность огибающей.
Подставив это выражение в предыдущее, получим:
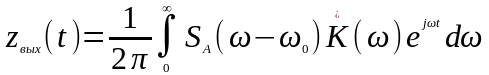 .
.
Перейдем к новой
переменной
 .
Тогда:
.
Тогда:
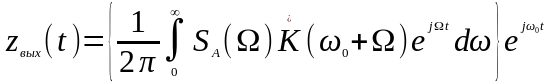 .
.
Выражение, стоящее в фигурных скобках, соответствует комплексной огибающей выходного колебания
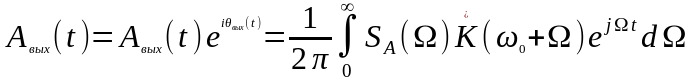 .
.
Дальнейшее упрощение
анализа вытекает из свойств передаточной
функции резонансных цепей, обладающих
сильно выраженной частотной
избирательностью. Модуль передаточной
функции
быстро убывает при удалении
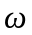 от резонансной частоты
от резонансной частоты
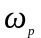 .
Поэтому передаточную функцию целесообразно
выражать в виде функции разности
.
Поэтому передаточную функцию целесообразно
выражать в виде функции разности
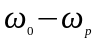 .
.
Введем новое обозначение передаточной функции:
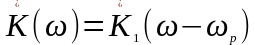 .
.
Подставив теперь
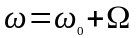 ,
получим
,
получим
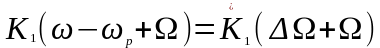 ,
,
где
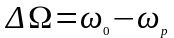
Так как при
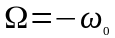 коэффициент передачи практически
равен нулю, нижний предел интеграла
можно заменить на
коэффициент передачи практически
равен нулю, нижний предел интеграла
можно заменить на
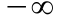 .
При этом выражение принимает следующий
вид:
.
При этом выражение принимает следующий
вид:
 .
.
Это выражение ничем не отличается от обычного интеграла Фурье, определяющего оригинал по заданной спектральной плотности огибающей и передаточной функции.
Заменив
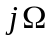 на
р, получим выражение в форме обратного
преобразования Лапласа
на
р, получим выражение в форме обратного
преобразования Лапласа
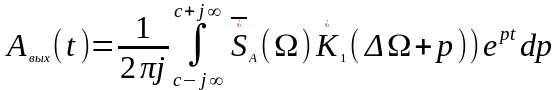 .
.
Вычисления,
связанные с определением
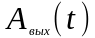 значительно проще, чем при непосредственном
определении
значительно проще, чем при непосредственном
определении
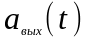 с помощью обратного преобразования
Лапласа, так как переход от
с помощью обратного преобразования
Лапласа, так как переход от
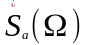 к
к
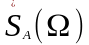 и от
и от
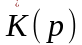 к
к
 сокращает
вдвое число особых точек подынтегральной
функции.
сокращает
вдвое число особых точек подынтегральной
функции.
Обратимся к общему выражению свертки и перепишем его в форме
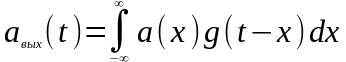
где
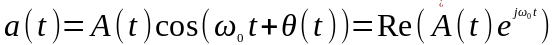 ,
а
,
а
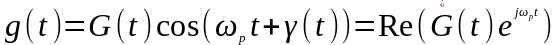 — импульсная
характеристика фильтра с резонансной
частотой
.
После подстановки, получим:
— импульсная
характеристика фильтра с резонансной
частотой
.
После подстановки, получим:
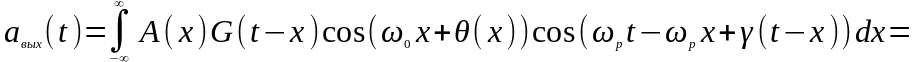
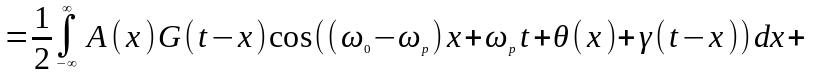
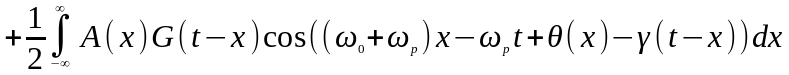 .
.
Вторым интегралом
можно пренебречь по сравнению с первым
из-за наличия быстропеременного множителя
с частотой
 .
Переходя к комплексной форме, получаем:
.
Переходя к комплексной форме, получаем:
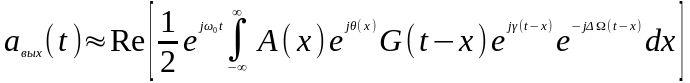 .
.
где .
Учитывая, что
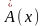 и
и
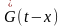 являются
комплексными огибающими соответственно
входного сигнала и импульсной
характеристики фильтра, приходим к
следующему выражению:
являются
комплексными огибающими соответственно
входного сигнала и импульсной
характеристики фильтра, приходим к
следующему выражению:
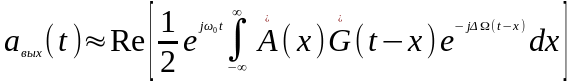 .
.
Из этого выражения вытекает, что комплексная огибающая выходного сигнала приближенно определяется половиной свертки комплексной огибающей входного сигнала с комплексной огибающей импульсной характеристики цепи:
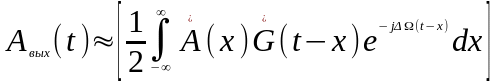
Последний множитель под интегралом учитывает расстройку центральной частоты спектра сигнала относительно резонансной частоты фильтра . При точной настройке:
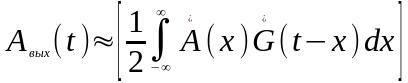 .
.
29
