
- •Основные радиотехнические процессы
- •Классификация цепей
- •Классификация сигналов
- •Характеристики детерминированных сигналов
- •Гармонический анализ периодических сигналов
- •Примеры спектров периодических сигналов
- •Распределение мощности в спектре периодического сигнала.
- •Гармонический анализ непериодических сигналов
- •Свойства преобразования Фурье
- •Примеры спектров непериодических сигналов
- •Распределение энергии в спектре непериодического сигнала
- •Соотношение между длительностью сигнала и широтой его спектра
- •Скорость убывания спектра вне основной полосы
- •Модуляция
- •Угловая модуляция.
- •Спектр колебания при угловой модуляции.
- •Спектр колебания при амплитудно-частотной модуляции
- •Узкополосный сигнал
- •Аналитический сигнал
- •Частотные и временные характеристики радиотехнических цепей
- •Апериодический усилитель
- •Резонансный усилитель
- •Обратная связь усилителя
- •Дифференцирующая и интегрирующая цепи
- •Спектральный метод.
- •Операторный метод
- •Метод интеграла наложения.
- •Метод огибающей.
- •Прохождение импульсного сигнала через дифференцирующие и интегрирующие цепи
- •Прохождение радиоимпульса через резонансный усилитель.
- •Прохождение ам – колебаний через резонансный усилитель.
- •Прохождение частотно – модулированного колебания через избирательные цепи.
- •Прохождение фазоманипулированного колебания через резонансную цепь.
Модуляция
Для передачи информации в радиотехнических каналах используются высокочастотные сигналы, параметры которых изменяются по закону несущего информацию управляющего сигнала.
Пусть дан сигнал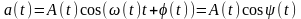 ,
изменение амплитуды сигнала A(t)
по закону управляющего сигнала называется
амплитудной модуляцией, изменение
,
изменение амплитуды сигнала A(t)
по закону управляющего сигнала называется
амплитудной модуляцией, изменение
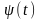 -
угловой модуляцией, причем изменение
-
угловой модуляцией, причем изменение
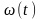 -
частотная модуляция, а изменение
-
частотная модуляция, а изменение
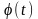 -
фазовая модуляция. Несущая частота w0
должна быть велика по сравнению с
наивысшей частотой спектра узкополосного
сигнала Wmax
(
-
фазовая модуляция. Несущая частота w0
должна быть велика по сравнению с
наивысшей частотой спектра узкополосного
сигнала Wmax
(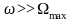 ).
).
Модулированное колебание имеет спектр, структура которого зависит как от спектра передаваемого сообщения, так и от вида модуляции.
Возможно существование нескольких видов модуляции: непрерывная, импульсная, кодоимпульсная.
Амплитудная модуляция
Характер огибающей A(t) определяется видом передаваемого сообщения.
Если сигнал сообщения , то огибающую модулированного колебания можно представить в виде
.
Где W — частота модуляции, g — начальная фаза огибающей, k — коэффициент пропорциональности, DАm=kS0 — абсолютное изменение амплитуды.
Отношение — коэффициент модуляции. Исходя из этого, можно записать:
.
Тогда амплитудно-модулированное колебание запишется в следующем виде
.
При неискаженной модуляции (М<1) амплитуда колебания изменяется в пределах от до .
Максимальному значению соответствует пиковая мощность (при М=1)
.
Средняя же за период модуляции мощность (при М=1)
.
Мощность для передачи амплитудно-модулированного сигнала требуется большая, чем для передачи немодулированного сигнала.
Спектр амплитудно-модулированного сигнала
Пусть модулированное колебание определяется выражением
Преобразуем это выражение
.
Из приведенного
выражения видно, что спектр
амплитудно-модулированного колебания,
при одноканальной модуляции состоит
из несущей частоты
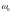 и двух боковых частот
и двух боковых частот
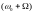 и
и
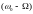 ,
амплитуда которых в
,
амплитуда которых в
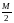 раз меньше амплитуды несущей частоты.
раз меньше амплитуды несущей частоты.
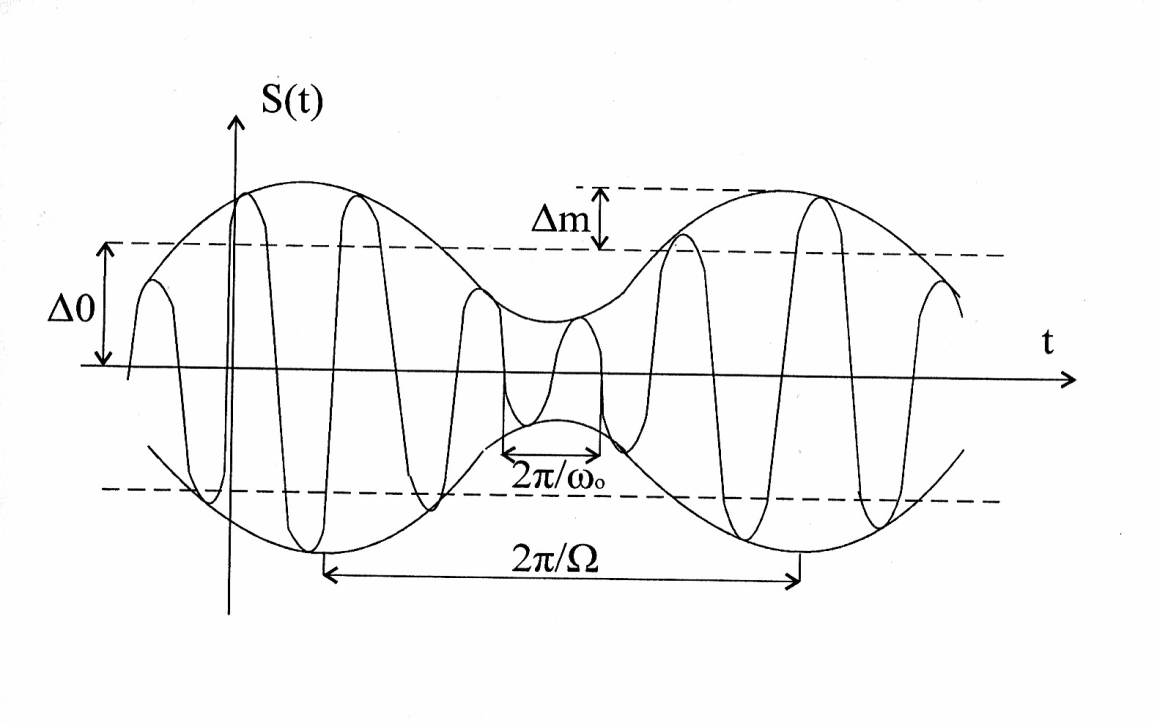
Спектр АМ-колебания
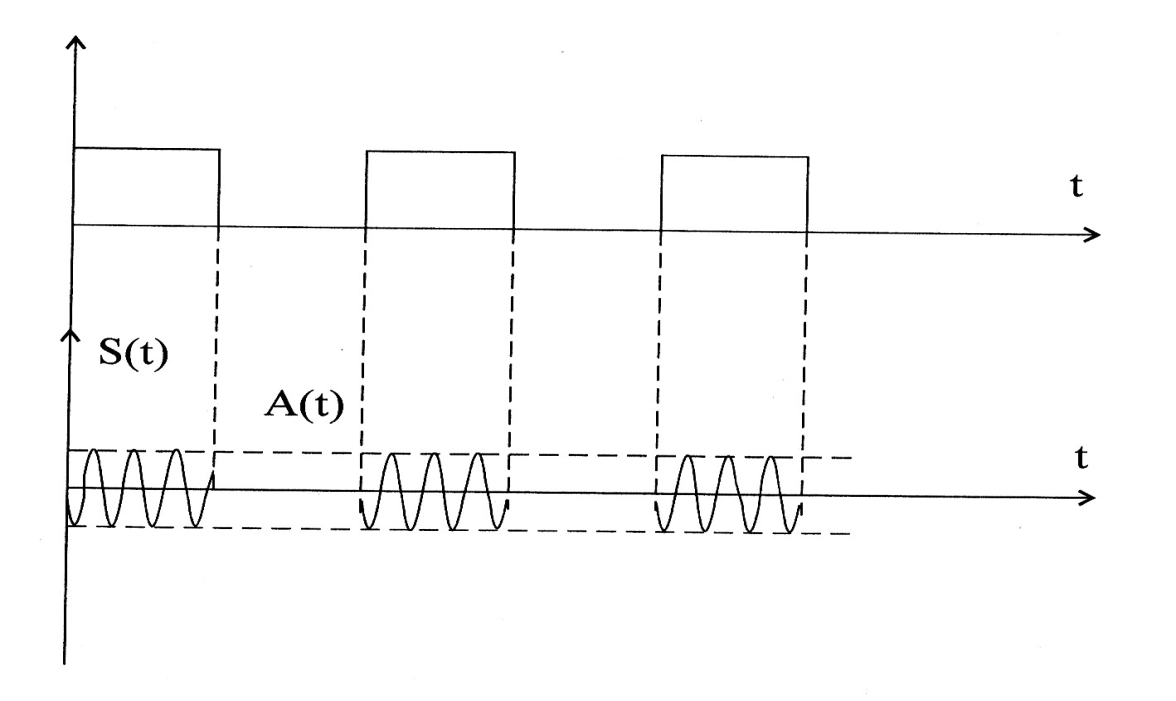
Радиоимпульс
Огибающая для тональной модуляции
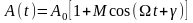 ,
тогда
,
тогда
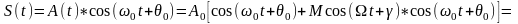
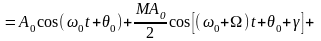
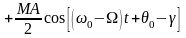
Векторная диаграмма иллюстрирует последнее выражение.
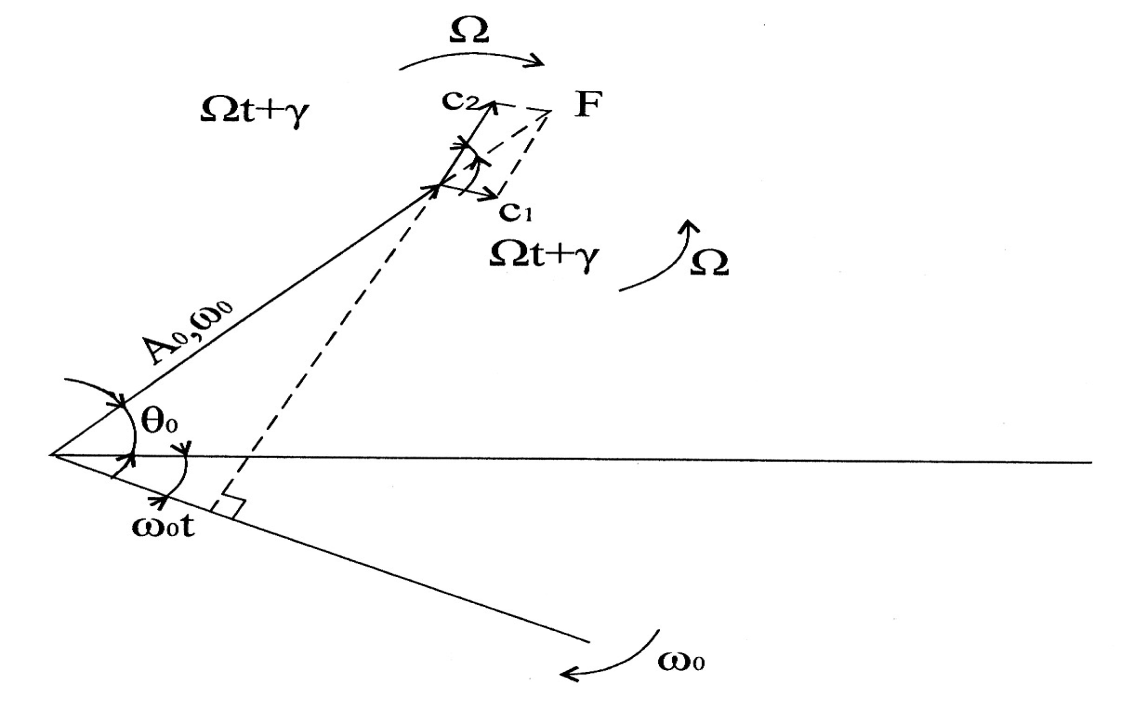
37, 38
Угловая модуляция.
Для простого гармонического колебания:
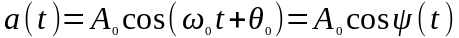
набег фазы за какой-либо конечный промежуток времени от t = t1 до t = t2 равен
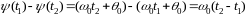
Отсюда видно, что
при постоянной угловой частоте набег
фазы за какой-либо промежуток времени
пропорционален длительности этого
промежутка. С другой стороны, если
известно, что набег фазы за время t2
– t1
равен
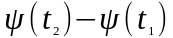 , угловую частоту можно определить как
отношение
, угловую частоту можно определить как
отношение
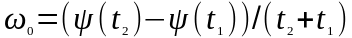 ,
если, конечно, имеется уверенность, что
в течение рассматриваемого промежутка
времени частота сохраняла постоянное
значение. Можно показать, что угловая
частота есть не что иное, как скорость
изменения фазы колебания.
,
если, конечно, имеется уверенность, что
в течение рассматриваемого промежутка
времени частота сохраняла постоянное
значение. Можно показать, что угловая
частота есть не что иное, как скорость
изменения фазы колебания.
Переходя к сложному колебанию, частота которого может изменяться во времени, выражения необходимо заменить интегральным и дифференциальным соотношениями
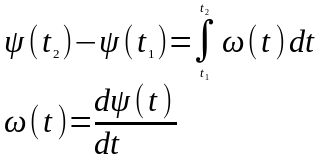
В этих выражениях
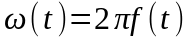 — мгновенная угловая частота колебания;
f(t)
— мгновенная частота.
— мгновенная угловая частота колебания;
f(t)
— мгновенная частота.
Полную фазу высокочастотного колебания в момент t можно определить как:
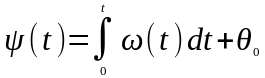 ,
,
где первое слагаемое
в правой части определяет набег фазы
за время от начала отсчета до
рассматриваемся момента времени,
 начальная фаза колебания.
начальная фаза колебания.
При таком подходе
фазу следует заменить на соотношение
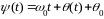 .
.
Итак, общее выражение для высокочастотного колебания, амплитуда которого постоянна, а аргумент модулирован, можно представить в форме:
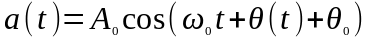
Соотношения, устанавливающие связь между изменениями частоты и фазы, указывают на общность двух разновидностей угловой модуляции — частотной и фазовой.
Поясним эти соотношения на примере простейшей гармонической ЧМ, когда мгновенная частота колебания определяется выражением
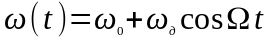
где
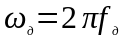 представляет собой амплитуду частотного
отклонения. Для краткости
представляет собой амплитуду частотного
отклонения. Для краткости
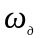 в дальнейшем будем называть девиацией
частоты или просто девиацией. Через
в дальнейшем будем называть девиацией
частоты или просто девиацией. Через
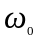 и
и
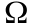 ,
как и при АМ, обозначены несущая и
модулирующая частоты.
,
как и при АМ, обозначены несущая и
модулирующая частоты.
Составим выражение для мгновенного значения колебания (тока или напряжения), частота которого изменяется, а амплитуда постоянна.
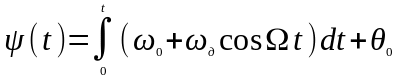
Выполнив
интегрирование, найдем
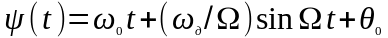 .
Таким образом:
.
Таким образом:
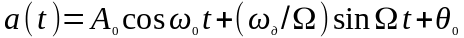 .
.
Фаза колебания
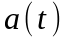 наряду с
линейно-возрастающим слагаемым
наряду с
линейно-возрастающим слагаемым
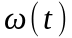 содержит
еще периодическое слагаемое
содержит
еще периодическое слагаемое
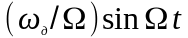 .
Это позволяет рассматривать
как колебание, модулированное
по фазе. Закон
этой модуляции является интегральным
по отношению к закону изменения частоты.
Именно модуляция частоты по
косинусноидальному закону приводит к
модуляции фазы по закону
синусоидальному. Амплитуду изменения
фазы
.
Это позволяет рассматривать
как колебание, модулированное
по фазе. Закон
этой модуляции является интегральным
по отношению к закону изменения частоты.
Именно модуляция частоты по
косинусноидальному закону приводит к
модуляции фазы по закону
синусоидальному. Амплитуду изменения
фазы
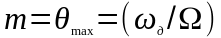 часто называют индексом угловой
модуляции.
часто называют индексом угловой
модуляции.
Заметим, что индекс модуляции совершенно не зависит от средней (немодулированной) частоты , а определяется исключительно девиацией и модулирующей частотой.
При
гармоническом модулирующем сигнале
различие между ЧМ и ФМ можно выявить,
только изменяя
частоту модуляции.
При ЧМ
девиация ωд
пропорциональна
амплитуде модулирующего напряжения
и не зависит от частоты модуляций.
При ФМ величина
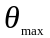 пропорциональна
амплитуде модулирующего напряжения и
не зависит от частоты модуляции.
пропорциональна
амплитуде модулирующего напряжения и
не зависит от частоты модуляции.
При ЧМ
,
зависящая, как указывалось выше, только
от амплитуды, будет, постоянной величиной,
а индекс модуляции
с увеличением частоты будет убывать.
При ФМ m
не зависит
от
,
а
 изменяется пропорционально частоте
модуляции.
изменяется пропорционально частоте
модуляции.
Кроме структуры колебания (при модуляции сложным сигналом) частотная и фазовая модуляции различаются и способом осуществления. При ЧМ обычно применяется прямое воздействие на частоту колебаний генератора. При ФМ генератор дает стабильную частоту, а фаза колебания модулируется в одном из последующих элементов устройства.
ЧМ ФМ
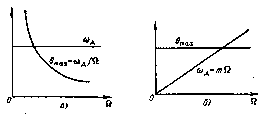
Зависимость индекса
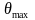 и девиации
и девиации
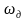 от модулирующей частоты при ЧМ
(а) и
ФМ (б).
от модулирующей частоты при ЧМ
(а) и
ФМ (б).
39
