§ 6.3. Основные числовые характеристики непрерывной случайной величины
1. Математическое ожидание непрерывной случайной величины определяется по формуле:
. (1.40)
2. Дисперсия непрерывной случайной величины определяется по формуле:
. (1.41)
3. Среднее квадратическое отклонение (1.38):
.
Приме 6.1. Задана функция распределения случайной величины Х:
.
Определить вероятность того, что в результате испытаний случайная величина примет значение большее 0,3, но меньшее 0,7. Найти плотность вероятности распределения случайно величины и ее дисперсию.
Решение.
По свойству интегральной функции распределения:
то есть
По определению плотности вероятностей случайной величины (1.39):
,
Вероятность попадания непрерывной случайной величины в определенный интервал может также быть найдена на основании свойства плотности распределения вероятностей:
,
т. е.
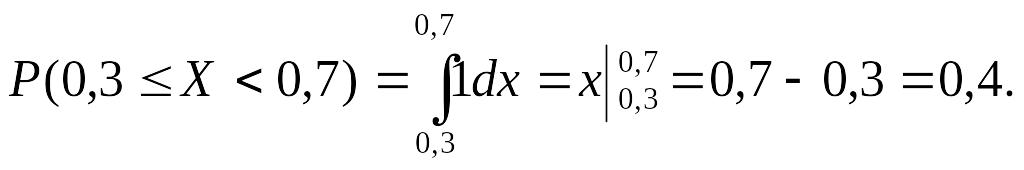
По определению (1.40) математическое
ожидание непрерывной случайной величины
равно:
.
По определению (1.41) дисперсия непрерывной случайно величины равна:
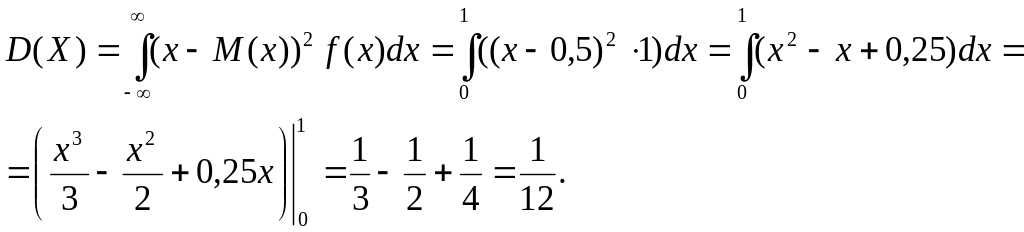
Кроме того, дисперсию можно вычислить и другим способом.
В соответствии с упрощенной формулой вычисления (1.32) дисперсия равна:
г
де
§ 6.4. Основные законы распределения непрерывных случайных величин
§ 6.4.1. Равномерный закон распределения
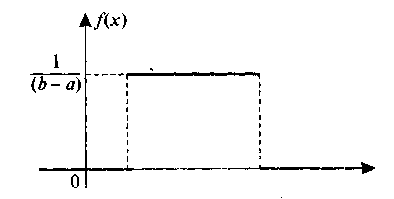
• Непрерывная случайная величина X имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, т. e.f(x) имеет вид:
.
Найдем постоянную величину С.
Учитывая
свойство функции плотности вероятности
,
получим:
,
откуда
,
а
.
Вычислим функцию распределения случайной величины с постоянной плотностью вероятностей.
По определению функции распределения и свойству плотности вероятности:
.
С=
а b x
Рис. 14. Функция плотности вероятности равномерного закона распределения
Так как функция плотности вероятности имеет три интервала с различными значениями, рассмотрим функцию распределения на каждом из этих интервалов:
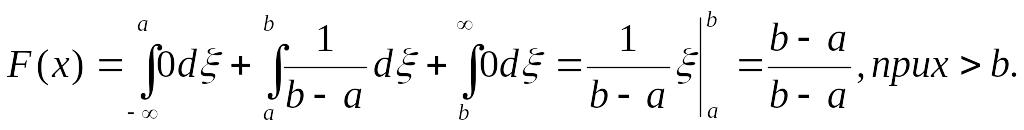
Следовательно, функция распределения случайноё величины, распределенной по равномерному закону на интервале [а; b] имеет вид:
.
Вероятность
попадания случайной величины,
распределенной по равномерному закону
на интервале (а; b),
в часть интервала
равна:
.
Рис. 15. Функция распределения равномерного закона распределения
Найдем числовые характеристики случайной величины, распределенной по равномерному закону.
По определению математическое ожидание равно:
Вычислим дисперсию в соответствии с упрощенной формулой:
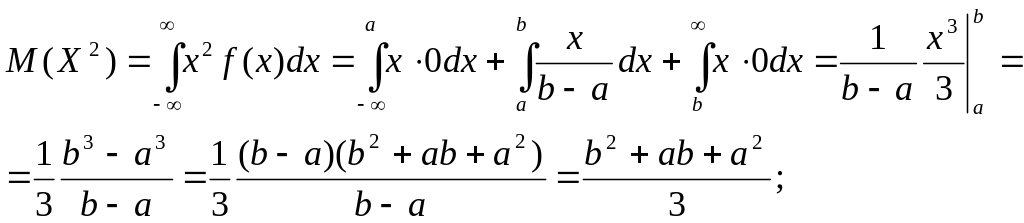
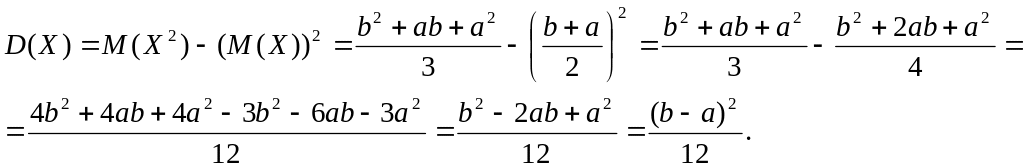
Математическое ожидание и дисперсия непрерывной случайной величины Х, имеющей равномерный закон распределения равны:
Пример 6.2. Время ожидания ответа абонента на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 2 минут. Найти интегральную и дифференциальную функции распределения этой случайной величины, среднее время ожидания ответа и среднее квадратическое отклонение. Определить вероятность того, что время ожидания ответа не превысит 1 минуты.
Решение.
Случайная величина Х – время ожидания ответа абонента на телефонный звонок – подчиняется равномерному закону распределения в интервале от 0 до 2 минут. Следовательно, ее плотность вероятности и функция распределения имеют вид:
;
.
По формуле математического ожидания равномерно распределенной случайной величины, среднее время ожидания ответа составит:
,
а среднее квадратическое отклонение:
Вероятность того, что время ожидания ответа не превысит 1 минуты, составит:
