§ 5.2. Основные числовые характеристики дискретной случайной величины

1. Математическое ожидание дискретной случайной величины определяется по формуле:

. (1.35)

Если дискретная случайная величина принимает бесконечное счетное множество значений, то при условии, что ряд сходится:

. (1.36)

2. Дисперсия дискретной случайной величины определяется по формуле:

. (1.37)

3. Среднее квадратическое отклонение:

. (1.38)

С реднее квадратическое отклонение было введено как дополнительная характеристика рассеяния значений случайной величины вокруг ее математического ожидания и, в отличие от дисперсии, совпадающая по размерности со случайной величиной.

Пример 5.2. Вероятность всхожести семян некоторого растения равна 0,8. Составить закон распределения числа взошедших семян из трех посеянных. Найти математической ожидание и дисперсию этой случайной величины.

Решение.

Случайная величина Х – число взошедших семян из трех посеянных. Х может принимать числовые значения: Для определения вероятностей рассмотрим соответствующие события.

Событие состоит в том, что из трех посеянных семян не взошло ни одного. Таким образом, проводится 3 независимых испытания, состоящих в проверке всхожести семени. Для каждого из 3 семян вероятность события А – семя взошло – по условию постоянна и равна:

Так как испытания удовлетворяют условиям схемы Бернулли (всхожесть отдельных семян есть события независимые), а n=3 – мало, то вероятность того, что из 3 посеянных семян не взошло ни одного, т. е. вероятность , определим по формуле Бернулли (1.24):

Аналогично:

Таким образом, закон распределения числа взошедших семян из трех посеянных имеет вид:

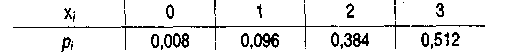
Правильность составления закона подтверждается равенством:

Найдем числовые характеристики построенной случайной величины.

1. По определению (1.35), математическое ожидание равно:

2. По определению дисперсии (1.37):

В соответствии с упрощенной формулой вычисления (1.32) дисперсия равна:

Найдем математическое ожидание случайной величины :

Т огда

Пример 5.3. Случайная величина X задана законом распределения:

Найти третье значение случайной величины и его вероятность, если известно, что ее математическое ожидание равно 2.

Решение.

По свойству ряда распределения отсюда

По определению математического ожидания (1.35) дискретной случайной величины:

О тсюда

Пример 5.4. Среди 8 часов, поступивших в ремонт, 2 с поломками оси. Наудачу взяты 3 часов. Составить закон распределения числа часов с поломками оси среди взятых трех.

Решение.

Случайная величина Х – число часов с поломками оси среди трех часов случайно выбранных из восьми. Таким образом, проводится отбор 3 часов из 8, которые можно разделить на две группы однотипных предметов: 2 с поломками оси, остальные – с прочими дефектами.

X может принимать числовые значения: с вероятностями , равными:

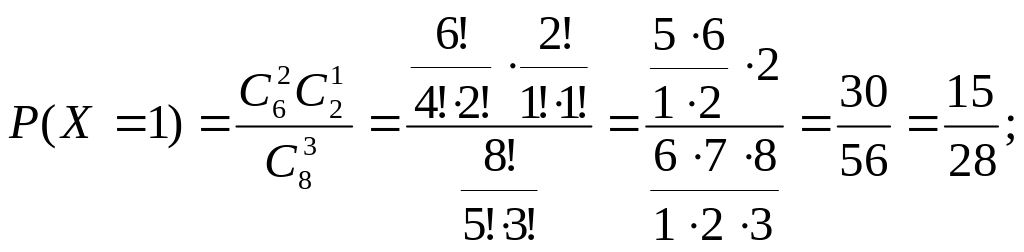
Теперь закон распределения числа часов с поломками оси среди трех часов случайно выбранных из восьми имеет вид:

Правильность составления закона подтверждается равенством:

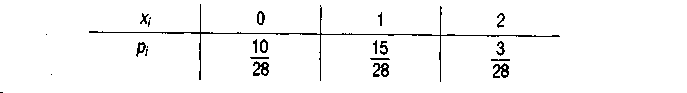
Пример 5.5. Даны независимые случайные величины X и Y заданные законами распределения:

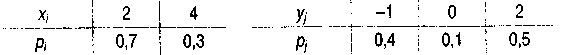
Составить закон распределения их суммы и проверить выполнение свойства математического ожидания М(Х+У)=М(Х)+М(У).

Решение.

Обозначим новую случайную величину Z=X+Y.

Для решения задачи (построения ряда распределения Z) построим вспомогательную таблицу:

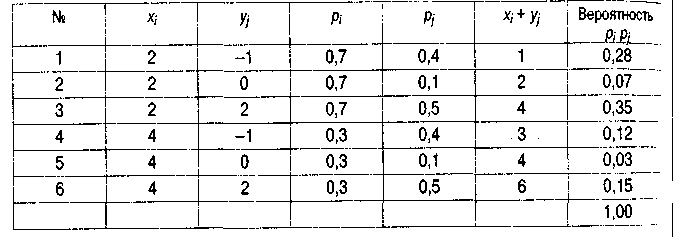
Следовательно, ряд распределения Z имеет вид:

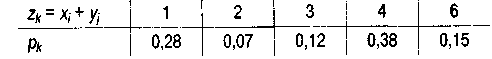
По определению (1.35) математическое ожидание дискретной случайной величины равно:

С другой стороны, М(Х)+M(Y)=2,6+0,6=3,2 – следовательно, свойство математического ожидания справедливо.