§ 7.4. Свойства случайной величины, имеющей нормальный закон распределения

1. Если , то для нахождения вероятности попадания этой величины в заданный интервал используется формула:

. (1.46)

Д оказательство.

Действительно, по свойству функции распределения любой непрерывной случайной величины, и, используя формулу для вычисления функции распределения случайной величины (1.43), можно записать:

,

г де .

Для односторонних и симметричных интервалов, используя формулу для вычисления функции распределения нормально распределенной случайной величины (1.43), можно вывести формулы:

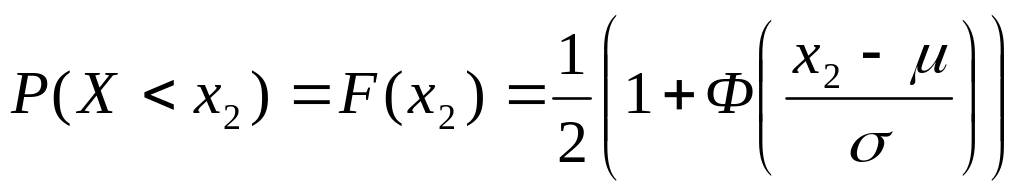; (1.47)

. (1.48)

2. Вероятность того, что отклонение случайной величины от ее математического ожидания не превысит величину (по абсолютной величине), равна:

. (1.49)

Д оказательство.

Используя формулу (1.46) и свойство нечетности Лапласа, получим:

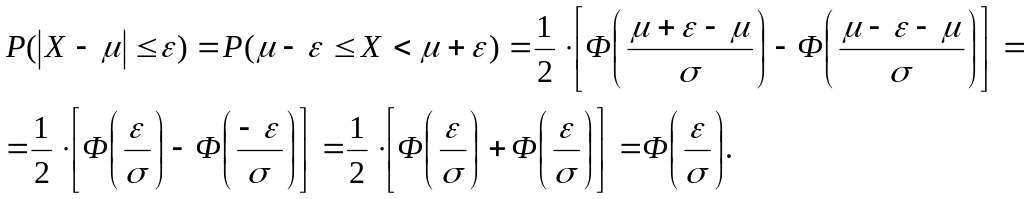
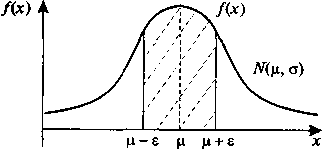
Рис. 22. Вероятность отклонения от среднего значений случайной величины Х, имеющей нормальный закон распределения

3. «Правило трех сигм».

Если случайная величина Х имеет нормальный закон распределения , то практически достоверно, что ее значения заключены в интервале (Вероятность «выброса» равна 0,0027).

Д оказательство.

Используя формулу (1.49) и таблицу значений функции Лапласа (табл. 1 Приложений), получим:

Рис. 23. «Правило трех сигм» для случайной величины Х, имеющей нормальный закон распределения

«Правило трех сигм» позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практических значений.

П ример 7.1. При сортировке случайные значения веса зерна распределены нормально со средним значением 0,15 г и средним квадратическим отклонением 0,03 г. Нормальные всходы дают зерна, вес которых более 0,10 г. Определить:

а) процент семян, от которых следует ожидать нормальные всходы;

б) величину, которую не превзойдет вес отдельного зерна с вероятностью 0,99.

Решение.

Обозначим случайную величину X – вес случайно отобранного зерна. По условию, X распределена по нормальному закону с математическим ожиданием 0,15 и средним квадратическим отклонением 0,03, т. е. .

а) Процент семян, от которых следует ожидать нормальные всходы – это вероятность получить нормальный всход от взятого наугад зерна. По условию, нормальный всход дают зерна, вес зерна которых удовлетворяет X>0,10. Вероятность этого события:

По таблицам значений функции Лапласа, учитывая, что Ф(-t)=-Ф(t) получим:

Ф(-1,67)=-0,9051, откуда т. е. от 95,2% семян следует ожидать нормальных всходов.

б) Пусть – величина, которую не превзойдет вес отдельного зерна с вероятностью 0,99, т. е.

С другой стороны, вероятность 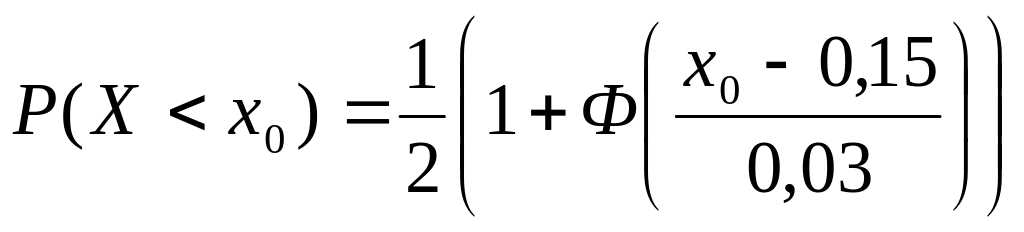, следовательно откуда и

По таблицам значений функции Лапласа: , откуда получаем

Таким образом, с вероятностью 0,99 вес взятого наугад зерна не будет превышать 0,22 г.

П ример 7.2. Случайные отклонения диаметра детали, выпускаемой цехом, от номинала распределены нормально. Математическое ожидание диаметра детали равно 20 мм, а дисперсия 0,36 мм. Найти:

а) вероятность того, что диаметр наудачу взятой детали имеет размеры от 19 до 22 мм;

б) вероятность того, что диаметр наудачу взятой детали отличается от математического ожидания не более чем на 1 мм (по абсолютной величине);

в) границы, в которых с вероятностью 0,9876 следует ожидать величину диаметра детали.

Решение.

Обозначим случайную величину X - диаметр случайно отобранной детали. По условию, X распределена по нормальному закону с математическим ожиданием 20 и дисперсией 0,36, т. е.

А. Вероятность того, что диаметр наудачу взятой детали имеет размеры от 19 мм до 22 мм, т. е. 19<X<22, определим по формуле:

По таблицам значений функции Лапласа, Ф(3,33)=0,9991 и так как Ф(-t) =-Ф(t): Ф(-1,67)=-0,9051, откуда .

Б. Вероятность того, что диаметр наудачу взятой детали отличается от математического ожидания не более чем на 1 мм (по абсолютной величине), т. е. , определим по формуле:

По таблицам значений функции Лапласа Ф(1,67)=0,9051, следовательно:

В. Пусть – величина отклонения диаметра случайно отобранной детали от среднего значения, определяет границы симметричного относительно математического ожидания интервала, в который с вероятностью 0,9876 попадает случайная величина Х, т. е.

С другой стороны, вероятность , следовательно,

П о таблицам значений функции Лапласа: отсюда получаем Таким образом, с вероятностью 0,9876 диаметр отобранной наугад детали будет находиться в пределах (20-1,5; 20+1,5), т. е. от 18,5 мм. до 21,5 мм.

Пример 7.3. Результат взвешивания химреактива распределен по нормальному закону со средним квадратическим отклонением веса 0,02 г. Какое отклонение массы реактива можно гарантировать с вероятностью 0,2?

Решение.

Обозначим случайную величину Х – масса случайно взвешенного реактива. По условию, X распределена по нормальному закону со средним квадратическим отклонением 0,02, т. е.

Пусть – величина отклонения массы случайно взвешенного реактива от среднего значения, s определяет границы симметричного относительно математического ожидания интервала, в который с вероятностью 0,2 попадает случайная величина X, т. е.

С другой стороны, вероятность , следовательно,

По таблицам значений функции Лапласа: , отсюда получаем

Таким образом, с вероятностью 0,2 отклонение массы реактива составит 0,005 г.