§ 8.2. Центральная предельная теорема

Выше были рассмотрены различные формы закона больших чисел, которые, при всем своем разнообразии, утверждают одно: сходимость по вероятности тех или иных случайных величин к определенным постоянным.

Все формы центральной предельной теоремы посвящены другой аспекту — установлению условий, при которых возникает самый распространенный в случайных явлениях нормальный закон распределения. Важнейшее место занимает теорема Ляпунова.

Теорема Ляпунова⁵

Рассмотрим n независимых случайных величин , удовлетворяющих условиям:

1. все величины имеют определенные математические ожидания _й конечные дисперсии ;

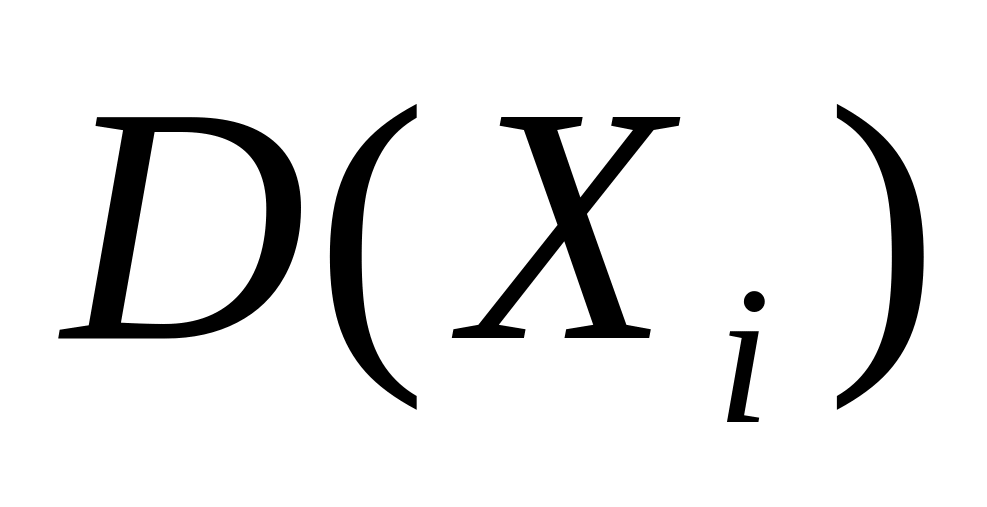2. ни одна из величин не выделяется резко среди остальных по своим значениям.

Тогда при неограниченном возрастании распределение случайной величины приближается к нормальному закону.

Таким образом, имеем следующую асимптотическую формулу:

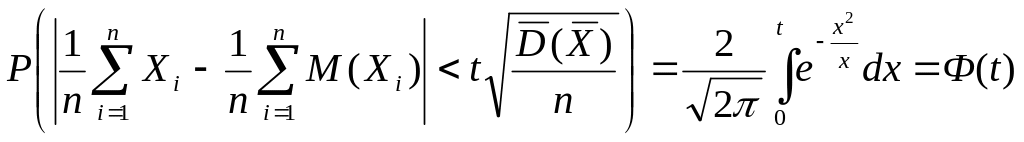, (1.56)

г де .

Пример 8.1. Дисперсия каждой из 400 независимых случайных величин равна 25. Найти вероятность того, что абсолютная величина отклонения средней арифметической случайных величин от средней арифметической их математических ожиданий не превысит 0,5.

Решение.

Применим теорему Ляпунова.

По условию задачи, n=400, =25, следовательно, =255 и =0,5.

П одставляя эти данные в формулу (1.56), , получим t=2, откуда по табл. 1 Приложений искомая вероятность .

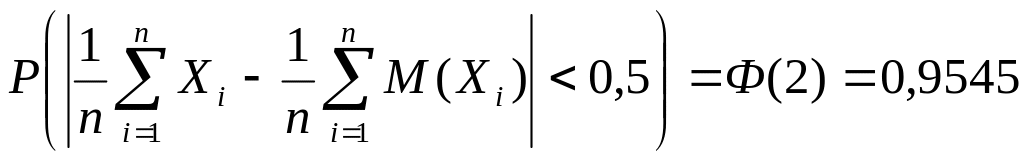Пример 8.2. Среднее количество вызовов наладчика станков, поступающих в течение часа в диспетчерскую, равно 21. Оценить вероятность того, что в течение часа поступит вызовов:

а) не менее 60;

б) менее 35.

Решение.

Случайная величина X – количество поступающих вызовов. X не принимает отрима тельных значений и, по условию, у нее существует математическое ожидание, равное М(Х)=21.

Поэтому в соответствии с неравенством Маркова (леммой Чебышева):

.

А. При а=60 получим оценку: Таким образом вероятность того, что в течение часа поступит не менее 60 вызовов не превышает 0,35.

Б. Так как , . При а=35 получима оценку:

Таким образом, вероятность того, что в течение часа поступит менее 35 вызовов –не менее 0,4.

П ример 8.3. Электрическая подстанция обслуживает сеть с 1 0 000 ламп, вероятность включения каждой из которых вечером равна 0,6. Оценить вероятность того, что число одновременно включенных ламп будет находиться в пределах от 5900 до 6100 включительно.

Решение.

Случайная величина Х – число одновременно включенных ламп. Так как вероятность включения каждой из лампочек есть величина постоянная, и при этом включение каждой лампочки является независимым событием, то X распределена по биномиальному закону. Поэтому ее числовые характеристики:

М(Х)=np=10000*0,6=6000,

D(X)=npq=10000*0,6*0,4=2400.

Событие, состоящее в том, что случайная величина X будет находиться в пределах от 5900 до 6100 включительно, означает:

т.е.

Так как для случайной величины X существует математическое ожидание и ограниченная дисперсия, то в соответствии с неравенством Чебышева:

.

По данным задачи получаем:

З начит вероятность того, что число одновременно включенных ламп будет находиться в пределах от 5900 до 6100 включительно, не менее 0,76.

Пример 8.4. Игральная кость подбрасывается один раз. Число выпавших очков есть случайная величина X. Определить вероятность того, что она примет значение меньшее 5, и оценить эту вероятность, пользуясь законом больших чисел.

Решение.

Случайная величина X- число очков, выпавших на кости, Х может принимать значения Вероятности определим в соответствии с классическим определением вероятности. Все возможные случаи представляют собой все возможные числа на верхней грани кости. Эти случаи равновозможны и несовместимы. Число всех возможных случаев N равно 6. Событие представляет собой выпадение на верхней грани кости числа . Число случаев М, благоприятствующих событию , равно 1. В соответствии с классическим определением вероятность события :

Таким образом, закон распределения случайной величины Х задается рядом распределения:

	1	2	3	4	5	6

Событие, состоящее в том, что число выпавших на кости очков примет значение меньшее 5, означает: (X<5)=(X=1)+(X=2)+(X=3)+(X=4). Так как события (X=1), (X=2), (X=3) и (X=4) несовместимы, то по теореме сложения для несовместимых событий:

По определению математического ожидания дискретной случайной величины,

Таким образом, случайная величина X не принимает отрицательных значений и у нее существует математическое ожидание: М(Х)=3,5.

Поэтому, в соответствии с неравенством Маркова (леммой Чебышева):

, а .

При а=5 получим оценку:

Таким образом, вероятность того, что число выпавших на кости очков примет значение меньшее 5, не менее 0,3.

Т о есть оценка вероятности, полученная с помощью закона больших чисел, не противоречит ее точному значению (0,6667>0,3).

П ример 8.5. Вероятность того, что изготовленный прибор удовлетворяет стандарту равна 0,9. Оценить наименьшее количество приборов, которое следует отобрать, чтобы доля стандартных приборов отличалась от вероятности не более чем на 0,0з (по абсолютной величине) с вероятностью, не меньшей 0,85.

Решение.

m/n – доля стандартных приборов среди отобранных. При этом вероятность удовлетворять стандарту каждого из приборов есть величина постоянная (р= ,9), и удовлетворение стандарту каждого прибора являются независимыми событиями. Поэтому в соответствии с теоремой Бернулли:

.

По данным задачи: =0,03;р=0,9; q=1-0.9=0,1 Р 0,85.

Следовательно,

Т аким образом, наименьшее количество приборов, которое следует отобрать, чтобы доля стандартных приборов отличалась от вероятности не более чем на 0,03 (по абсолютной величине) с вероятностью, не меньшей 0,85, составляет 667.

1 Бернулли (Bernoulli) Якоб (1654-1705) – швейцарский ученый-математик, профессор математики Базельского университета, родоначальник знаменитой семьи ученых.

2 Муавр (Moivre) Абрахам де (1667-1754) – английский математик. Лаплас (Laplace) Пьер Симон (1749-1827) – французский астроном, математик и физик. Теорема доказана П. Лапласом в книге «Аналитическая теория вероятностей» (1812). Один частный случай был известен ПА. Муавру (1730), в связи с чем и называется теоремой Муавра – Лапласа.

3 Пуассон (Poisson) Симеон Дени (1781-1840), французский ученый, выдающийся математик и физик, профессор Парижского университета.

4 Здесь и далее случайные величины обозначаются заглавными латинскими буквами, а принимаемые ими значения строчными.

5 Одна из наиболее общих форм центральной предельной теоремы была доказана русским математиком и механиком Александром Михайловичем Ляпуновым (1857-1918) в 1900 г.