Глава 5. Дискретная случайная величина

• Дискретная случайная величина — случайная величина, которая принимает конечное или бесконечное, но счетное число отдельных изолированных значений (т. е. их можно перенумеровать натуральными числами).

Понятие дискретной случайной величины тесным образом связано с понятием случайного события, являясь в некотором смысле его обобщением. При определении дискретной случайной величины первичным понятием также является испытание, результат которого характеризуется не альтернативным исходом (появится событие или нет), а некоторым числом (числом появления события в серии независимых испытаний; числом очков, выбиваемых стрелком; числом вкладчиков, посетивших отделение банка за определенный период времени, и т. д.).

Для дискретной случайной величины простейшей формой задания закона распределения является ряд распределения, представляющий собой таблицу, в верхней строке которой указаны возможные значения , дискретной случайной величины Х, а в нижней — соответственно вероятности , того, что X примет значение :

			…
			…

При построении ряда распределения необходимо помнить, что:

1. , по свойству вероятности ;

2. , так как события , , … , составляют полную группу попарно несовместных событий.

• Графическое представление ряда распределения называется многоугольником (полигоном) распределения.

.

х

Рис. 7. Полигон распределения дискретной случайной величины Х

Для его построения возможные значения дискретной случайной величины Х откладываются по оси абсцисс, а соответствующие вероятности — по оси ординат; точки с координатами ( ; ) соединяются отрезками.

§ 5.1. Функция распределения дискретной случайной величины

Другим способом представления закона распределения дискретной случайной величины является интегральная функция распределения или функция накопленных вероятностей.

• Функция распределения (интегральная функция) F(x) определяет для каждого возможного значения х вероятность того, что случайная величина X примет значение, меньшее х:

. (1.33)

• Функция распределения дискретной случайной величины F(x) равна сумме вероятностей всех значений х,, меньших заданного значениях:

. (1.34)

Свойства интегральной функции распределения дискретной случайной величины:

1. Функция распределения может принимать любые значения от 0 до 1, так как по определению является вероятностью:

.

2. Интегральная функция распределения является неубывающей:

.

3. Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков равна 1. Эта функция кусочно постоянна на интервалах, на которых нет ее значений.

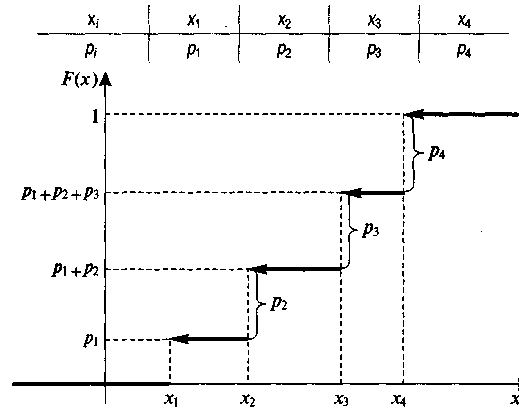
Рис. 8. Функция распределения дискретной случайной величины Х, принимающей 4 возможных значения.

4. Интегральная функция распределения дискретной случайной величины непрерывна слева:

,

.

5. Вероятность попадания дискретной случайной величины в интервал [а;b) равна приращению функции распределения в этих точках:

/

6. Если все возможные значения случайной величины X принадлежат интервалу то

7. Если все возможные значения дискретной случайной величины X расположены на всей числовой оси ОХ, то

(как вероятность невозможного события);

(как вероятность достоверного события).

Пример 5.1. Случайная величина Х задана законом распределения:

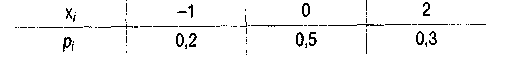
Решение.

По определению (1.33)

Если , то так как случайная величина не принимает ни одного значения, меньшего -1,F(x)=0.

Если , то в интервал ( ) попадает одно значение случайной величины х=-1 с вероятностью р=0,2, следовательно, .

Если , то в интервал ( ) попадает два значения случайной величины х=-1 с вероятностью р=0,2 и х=0 с вероятностью р=0,5, следовательно, по (1.34)

Если х>2, то в интервал ( ) попадают все значения случайной величины, следовательно,

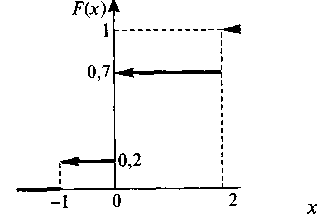
В итоге получаем интегральную функцию распределения: