Глава 7. Нормальный закон распределения

Рассмотрим еще один закон распределения непрерывной случайной величины, который, в силу его особой важности и исключительной роли в теории вероятностей, выносится в отдельную тему.

Нормальное распределение — наиболее часто встречающийся вид распределения. С ним имеют дело при анализе погрешностей ошибок, контроле технологических процессов, при анализе и прогнозировании различных экономических, социальных, демографических явлений. Наиболее важным условием возникновения нормального распределения является формирование признака как суммы большого числа независимых слагаемых, ни одно из которых не характеризуется исключительно большой по сравнению с другими дисперсией.

Еще одна причина, обусловливающая особое место этого закона распределения среди других, и главная особенность нормального распределения состоит в том, что оно является предельным, к которому с ростом числа наблюдений стремятся другие распределения.

Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами р. и о (обозначают ), если ее плотность вероятности имеет вид:

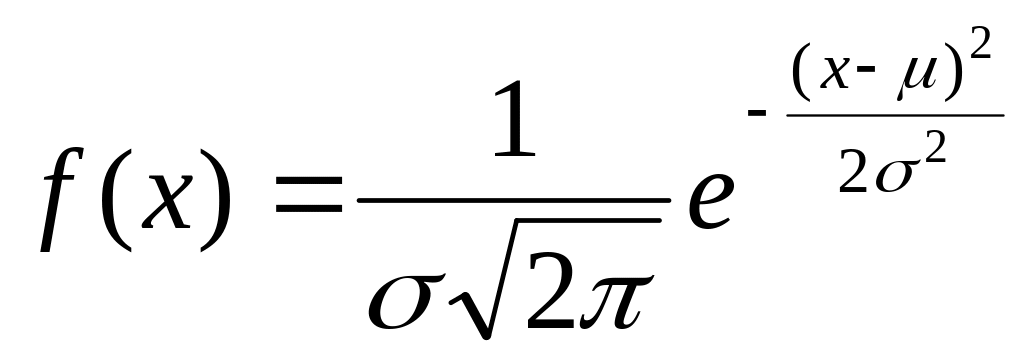, (1.42)

где – математическое ожидание Х,

– дисперсия ( – среднее квадратическое отклонение).

§ 7.1. Свойства функции плотности вероятности (кривой Гаусса) нормального закона распределения

1. существует при любых действительных Х.

2. .

3. Максимальное значение принимает в точке , при этом .

Рис. 16. Функция плотности вероятности (кривая Гаусса) нормального закона распределения

4. Кривая плотности нормального закона распределения симметрична относительно прямой .

5. Кривая плотности нормального закона распределения имеет две точки перегиба с координатами: .

§ 7.2. Математическое ожидание и дисперсия нормальной случайной величины

Рассмотрим, как будет изменяться кривая плотности вероятности нормального закона при изменении ее параметров — и .

Математическое ожидание или среднее значение ц характеризует центр рассеивания значений случайной величины и при изменении при неизменной дисперсии кривая будет смешаться вдоль оси абсцисс, не меняя своей формы (рис. 17).

Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, которая характеризует рассеяние значений случайной величины вокруг ее среднего, то кривая будет изменять свою форму, сжимаясь или растягиваясь, (так как площадь под ней должна оставаться единичной) не сдвигаясь вдоль оси абсцисс (рис. 18).

Таким образом, параметр (математическое ожидание) характеризует положение, а параметр (дисперсия) — форму кривой плотности вероятности.

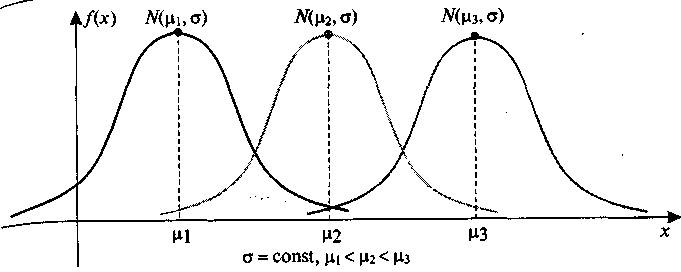
Рис. 17. Сравнение плотности вероятности трех нормальных случайных величин с разными математическими ожиданиями, но одинаковыми дисперсиями

Рис. 18. Сравнение плотности вероятности трех нормальных случайных величин с одинаковыми математическими ожиданиями, но разными дисперсиями.

§ 7.3. Функция распределения случайной величины, распределенной по нормальному закону

Вычислим функцию распределения случайной величины, имеющей нормальный закон распределения.

По определению функции распределения:

.

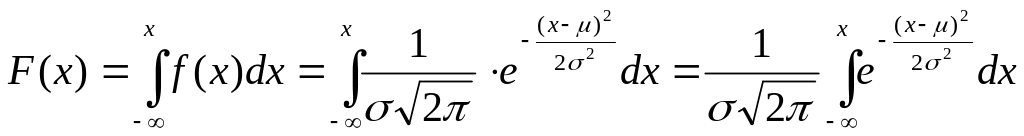Сделаем замену переменных и получим:

.

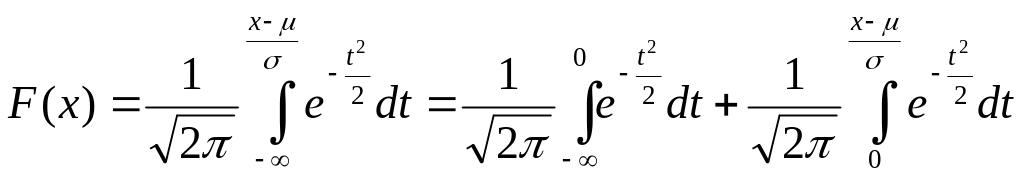Первый интеграл, используя четность подынтегральной функции и то, что интеграл Эйлера – Пуассона равен , можно вычислить:

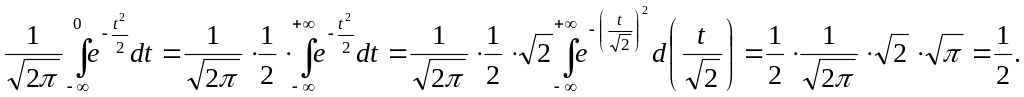
Таким образом, можно записать: .

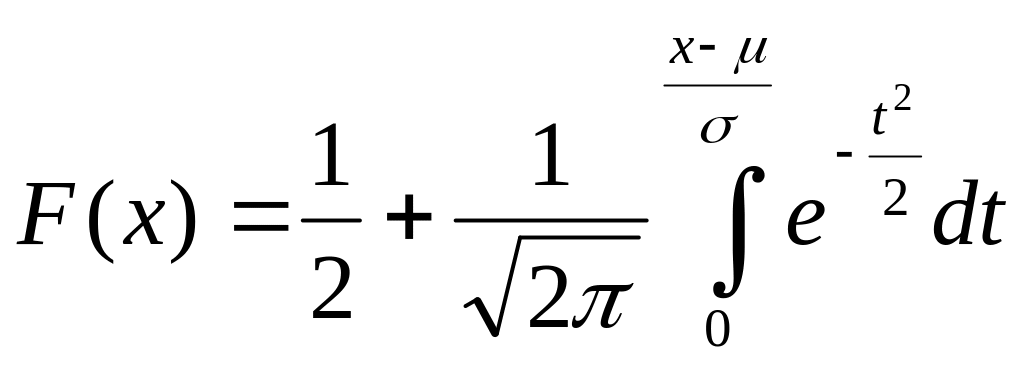Интеграл такого рода не выражается в элементарных функциях, но для — его нахождения используют особую функцию, так называемый интеграл вероятностей или функцию Лапласа, *" для которой составлены таблицы. Существует много разновидностей таких функций, например:

,

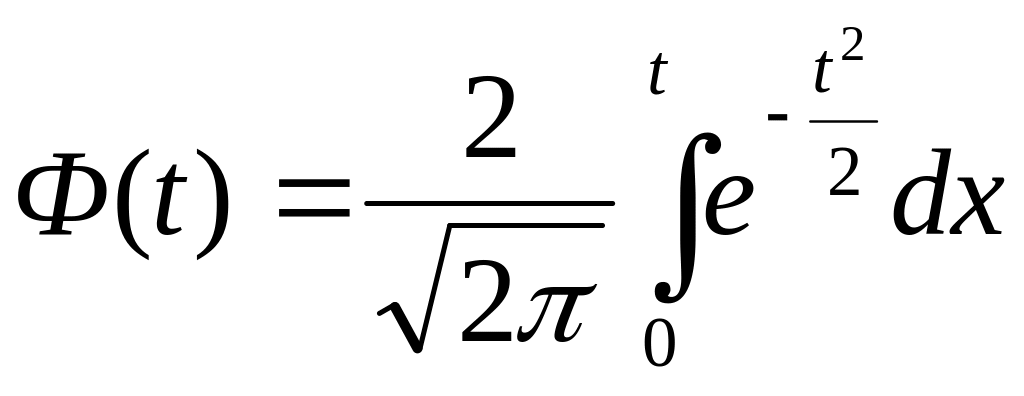значения которой приведены в табл. 1 Приложений.

Именно такой вид функции Лапласа будем использовать далее.

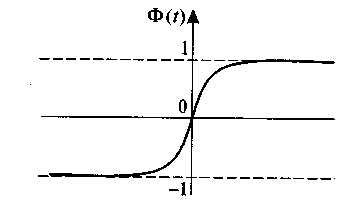
Рис. 19. Функция Лапласа (интеграл вероятностей) Ф(t)

1. Ф(t) — нечетная функция, т.е. Ф(-t)=-Ф(t).

2. Ф(t) — монотонно возрастающая функция, т. е. при ; при t>5 можно считать .

Итак, используя интеграл вероятностей или функцию Лапласа Ф(t) можно выразить функцию распределения нормального закона.

х

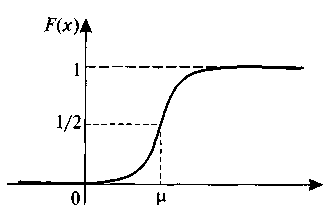
Рис. 20. Функция распределения нормального закона распределения

• Функция распределения случайной величины X, имеющей нормальный закон распределения с параметрами и , определяется по формуле:

, (1.43)

где – функция Лапласа (табл. 1 Приложений).

Стандартный нормальный закон распределения

Рассмотрим очень важный частный случай нормально распределенной случайной величины.

• Нормальный закон распределения случайной величины Х с параметрами и 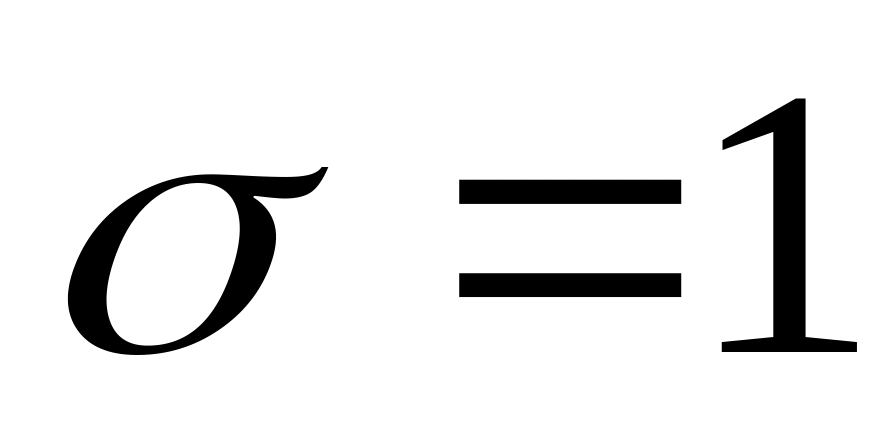(обозначается N(0;1)) называется стандартным или нормированным.

• Функция плотности вероятности стандартного нормального закона:

. (1.44)

• Функция распределения стандартного нормального закона:

, (1.45)

где – функция Лапласа (табл. 1 Приложений).

Значения функции плотности вероятности стандартного нормального закона или функции Гаусса представлены в табл. 7 Приложений.

Функция Гаусса:

1. f(t) – четная функция, т. е. f(t)=f(-t)/

2. 

   f(t) – монотонно убывающая функция, т. е. при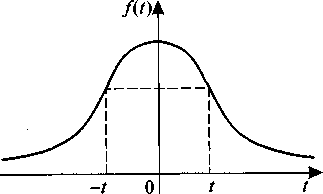 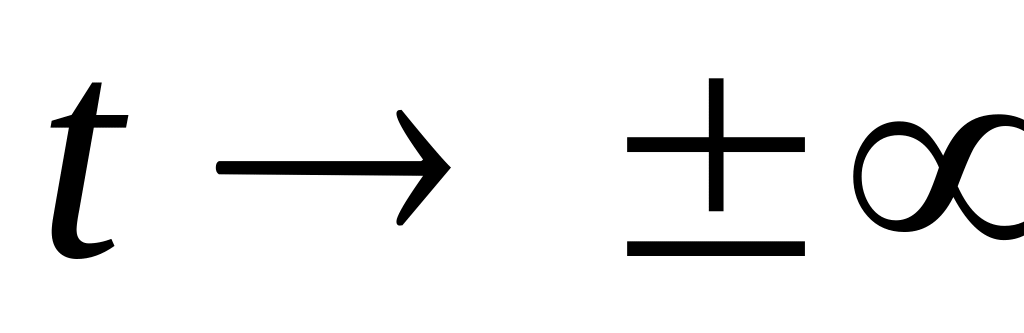; при t>5 можно считать .

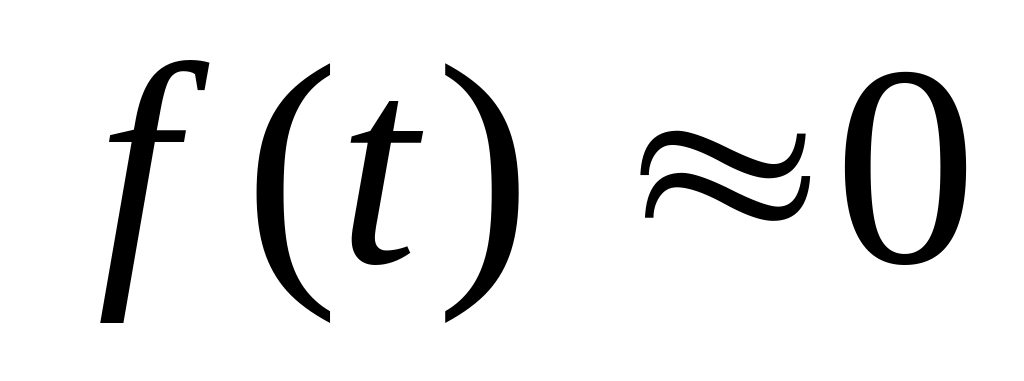Рис. 21. Функция Гаусса или плотности вероятности стандартного нормального закона распределения