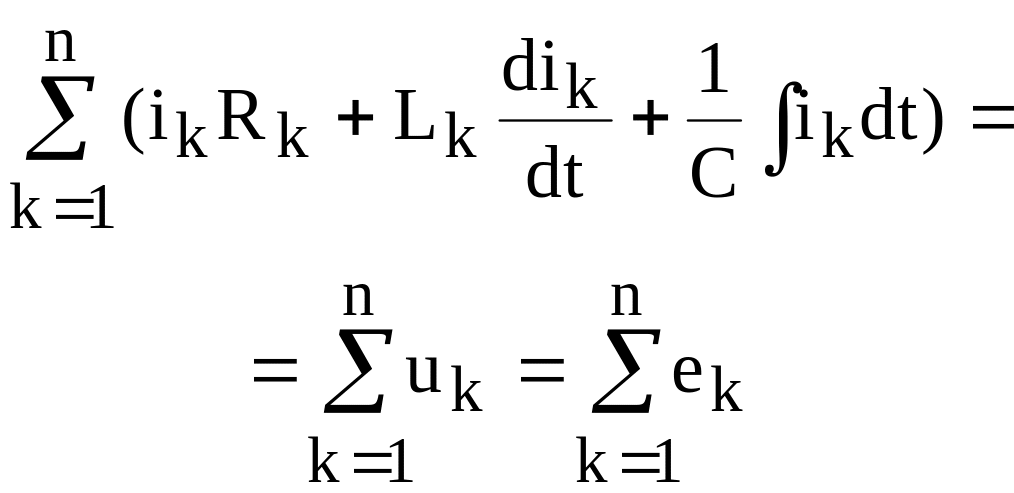- •А. М. Купцов
- •Основы теории цепей
- •Часть 1
- •Линейные электрические цепи
- •В ведение
- •I. Элементы и топологические свойства электрических цепей
- •Общие сведения и определения
- •Идеализированные схемные элементы электрической цепи
- •Линейные модели реальных элементов цепи
- •1.4. Схемы электрических цепей и их структура
- •1.5. Граф цепи. Топологические матрицы
- •1.6. Задачи исследования электрических цепей. Общие вопросы формирования уравнений
- •1.7. Общие свойства решений уравнений цепи
- •Основные методы расчета электричеких цепей
- •2.1. Комплексный метод
- •Метод наложения
- •Метод контурных токов
- •Порядок расчета цепи методом контурных токов
- •Метод узловых потенциалов
- •Правила записи узловых уравнений
- •Порядок расчета цепи методом узловых потенциалов
- •Метод эквивалентного источника
- •Эдс ег определяется напряжением на зажимах ab при размыкании ветви (режим холостого хода):
- •Методы узловых потенциалов и контурных токов в матричной форме
- •Порядок расчета цепи методом узловых потенциалов в матричной форме
- •Порядок расчета цепи методом контурных токов в матричной форме
- •Расчет электрических цепей с взаимной индуктивностью
- •В каждой из катушек индуктируется эдс, которая определяется собственным потокосцеплением kk и потокосцеплением связанной катушки :
Основные методы расчета электричеких цепей
Вынужденные составляющие в виде постоянной величины и периодической синусоидальной функции времени (частное решение дифференциального уравнения) называют установившимися составляющими, поскольку они характеризуют установившийся режим цепи после затухания свободной составляющей. Режим перехода цепи от одного установившегося состояния к другому принято называть переходным процессом или режимом.
Ниже рассматриваются методы расчета цепей в установившемся режиме.
2.1. Комплексный метод
Токи и напряжения, изменяющиеся во времени по синусоидальному закону, записывают:
![]() ,
,
где
![]() - амплитуда или максимальное значение,
- амплитуда или максимальное значение,
![]() )
– фаза, измеряемая в радианах или
градусах,
)
– фаза, измеряемая в радианах или
градусах,
![]() - начальная фаза,
определяющая значение функции при t
= 0,
- начальная фаза,
определяющая значение функции при t
= 0,
![]() - угловая частота
(рад/с), определяющая период колебаний
- угловая частота
(рад/с), определяющая период колебаний
![]() .
.
Число периодов в
секунду называют циклической или просто
частотой
![]() ,
измеряемой в герцах (Гц).
,
измеряемой в герцах (Гц).
Амплитуда, частота и начальная фаза полностью характеризуют синусоидально изменяющуюся величину, однако на практике для оценки действия синусоидальных токов и напряжений вводят действующее и среднее (по модулю) значения.
Действующим или среднеквадратичным называют величину:
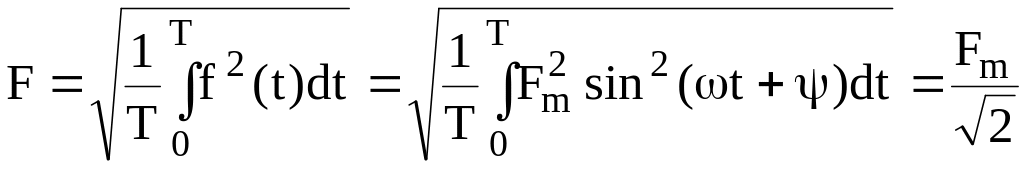 .
.
На действующие значения градуируются приборы, предназначенные для измерения переменных токов и напряжений.
Среднее значение по модулю определяется:
![]() .
.
На средние значения градуируются приборы, предназначенные для измерения постоянных токов и напряжений.
На рис. 2.1 показаны временной график синусоидальной функции (а) и ее векторное изображение или векторная диаграмма (б).
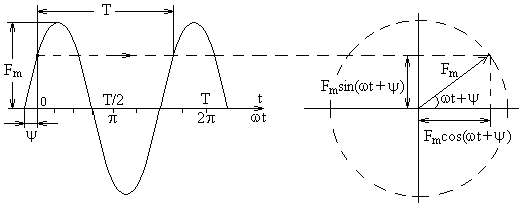
а б
Рис. 2.1
Нетрудно представить, что операции с синусоидальными токами и напряжениями, имеющими различные начальные фазы, в тригонометрической и графической формах сложны и громоздки. Поэтому широкое распространение получил комплексный (символический) метод.
Суть
его - в представлении синусоидальных
функций одинаковой частоты функциями
комплексной частоты. Для перехода от
функций времени к функциям комплексной
частоты используют формулу Эйлера:
![]() ,
где
,
где
![]() - мнимая единица (йот). Согласно этой
формуле,
- мнимая единица (йот). Согласно этой
формуле,
![]() , где
, где
![]() обозначает мнимую часть комплексного
числа, которое, в свою очередь, можно
представить
обозначает мнимую часть комплексного
числа, которое, в свою очередь, можно
представить
![]() .
Здесь
.
Здесь
![]() -
фазовый множитель, а
-
фазовый множитель, а
![]() - временной множитель.
- временной множитель.
Если
ввести в рассмотрение знак соответствия
![]() , то для фиксированного момента времени
t
= 0 будем иметь: f(t)
, то для фиксированного момента времени
t
= 0 будем иметь: f(t)
![]() .
Здесь
.
Здесь
![]() -
комплексная амплитуда;
-
комплексная амплитуда;
![]() - комплексное действующее значение
функции.
- комплексное действующее значение
функции.
При сложении (вычитании) комплексных чисел их записывают в алгебраической форме и отдельно складывают (вычитают) их действительные и мнимые части.
Например,
если
![]() ,
,
а
![]() ,
,
то
![]() ,
,
где
![]() ;
;
![]() .
.
Умножение и деление комплексных величин производят, как правило, в показательной форме:
![]() ;
;
![]() .
.
В комплексной форме дифференцирование по времени соответствует умножению, а интегрирование - делению комплексных значений рассматриваемых функций на j, так что:
![]()
![]()
![]() ;
;
![]()
![]() .
.
Величины XL и XC - индуктивное и емкостное сопротивления гармоническому току;
ZL и ZC – соответственно индуктивное и емкостное сопротивления в комплексной форме.
Для резистивного элемента напряжение в комплексной форме определяется:
uR = R i U mR = R I m = Z R I m ,
где ZR = R - величина вещественная.
Если пользоваться действующими значениями, тогда:
U R = Z R I ; U L = Z L I ; UC = ZC I.
Примеры определения входных (эквивалентных) комплексных сопротивлений двухполюсников, состоящих (образованных) из R, L, C – элементов приведены в табл. 2.1.
Таблица 2.1
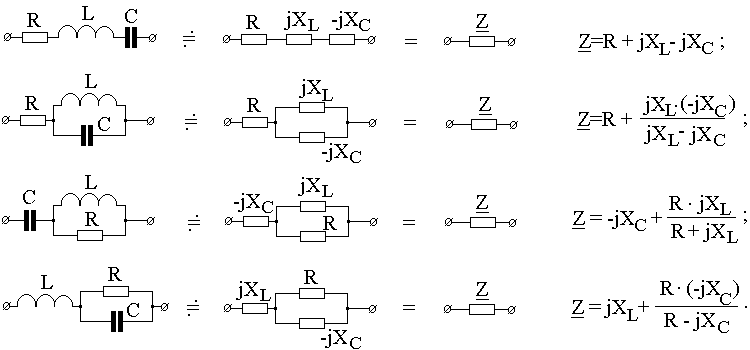
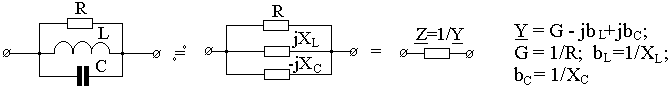
Величину,
обратную комплексному сопротивлению,
называют комплексной проводимостью
![]() .
Как следует из приведенной табл. 2.1, при
последовательном соединении пассивных
элементов суммируются алгебраически
их комплексные сопротивления, а при
параллельном – комплексные проводимости.
.
Как следует из приведенной табл. 2.1, при
последовательном соединении пассивных
элементов суммируются алгебраически
их комплексные сопротивления, а при
параллельном – комплексные проводимости.
Выражения комплексных сопротивления Z и проводимости Y для любого двухполюсника содержат информацию как о соотношении между действующими (амплитудными) значениями тока I и напряжения U, так и фазовом сдвиге между ними:
![]() ;
;
![]() .
.
Вещественная и мнимая части комплексного сопротивления представляют его активное R и реактивное X сопротивления:
![]() .
.
Аналогично вещественная и мнимая части комплексной проводимости Y представляют активную G и реактивную b проводимости:
![]() .
.
Нетрудно установить, что
![]() ;
;
![]() ;
;
![]() .
.
Соотношения между R, X, Z, G, b, y иногда изображают графически в виде треугольников сопротивлений и проводимостей, показанных на рис. 2.2, а и б соответственно.
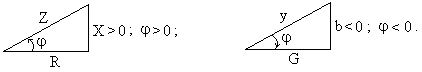
а б
Рис. 2.2
Согласно
рис. 2.2, активные и реактивные сопротивления
и проводимости без фазового множителя
![]() складывать н е л ь з я.
складывать н е л ь з я.
ПРИМЕР 2.1. Определите комплексную амплитуду тока, изменяющегося по закону i(t) = 10sin(100t + 300).
РЕШЕНИЕ. Комплексная амплитуда представляет собой функцию, модуль которой равен амплитуде заданной функции времени, а фазовый множитель еj определяется ее начальной фазой во временной области. Таким образом, I m = 10ej30 или в алгебраической форме I m = 8,65 + j5.
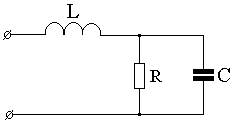
ПРИМЕР 2.2. Определить входные комплексные сопротивления цепи по рис. 2.3 с элементами R = 10 Ом; L = 50 мГн; С = 1 мФ на частотах 1 = 0 и 2 = 100 рад/с.
![]() .
Эквивалентное комплексное сопротивление
по отношению к входным зажимам:
.
Эквивалентное комплексное сопротивление
по отношению к входным зажимам:
Рис. 2.3
![]() .
.
Подставляя численные значения параметров элементов для частоты 1 = 0, получаем:
![]() Ом.
Ом.
Для частоты 2 = 100 рад/с имеем:
![]() Ом.
Ом.
ЗАМЕЧАНИЯ. 1. Сигнал с частотой 1 = 0 и периодом Т = является постоянным во времени, поэтому входное сопротивление данной цепи чисто вещественное, соответствующее сопротивлению R.
Отсутствие мнимой составляющей в комплексном сопротивлении Z(100) на частоте 2 = 100 рад/с объясняется взаимной компенсацией сопротивлений индуктивности и емкости.
Уравнения цепи в комплексной форме записывают на основе законов Кирхгофа, как показано в табл. 2.2.
Для однозначности записи уравнений цепи соблюдают следующие правила:
1. Положительные направления напряжений ветвей совпадают с произвольно выбранными положительными направлениями токов;
2. При записи первого закона Кирхгофа токи, выходящие из узла, считаются положительными, а входящие в узел - отрицательными;
Таблица 2.2
|
Для мгновенных значений |
В комплексной форме |
Закон Ома для ветви с ЭДС
|
|
|
Первый закон Кирхгофа для узлов |
|
|
Второй закон Кирхгофа для контуров |
или
|
или
|
3. При записи второго закона Кирхгофа положительным считают напряжение, направление которого совпадает с направлением обхода контура;
4. Положительные направления напряжения и тока на источниках энергии - противоположны.
Например, для узла, изображенного на рис. 2.4, а, следует записать:
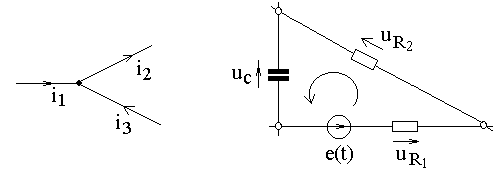
а б
Рис. 2.4
![]() или
или
![]() ,
,
если токи синусоидальные, одинаковой частоты.
Для контура, показанного на рис. 2.4, б, имеем:
![]() .
.
или
![]() .
.
Из первого закона Кирхгофа, в частности, следует:
![]() .
.
Это дает возможность определять один из токов по m-1 известным. Аналогичное равенство записывается и для второго закона Кирхгофа:
![]() .
.
ПРИМЕР 2.3. Определить ток i1 по рис. 2.4, а, если i2 = 3sint A; i3 = 4cost A.
РЕШЕНИЕ. На основании первого закона Кирхгофа
i1 = i2 - i3 = 3sint - 4cost.
Вычисления произведем комплексным методом, изобразив
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ,
,
тогда
![]() .
.
Переходя во временную область, получаем: i1 = 5sin(t - 53,130) А.
ПРИМЕР 2.4. Определить действующие комплексные значения токов I 3, I 5 и I 6 для фрагмента цепи, показанного на рис. 2.5, по заданным токам, изменяющимся по синусоидальному закону:
![]() А;
А;
![]() А;
А;
![]() А.
А.
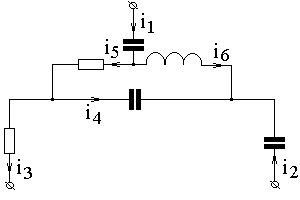
Рис. 2.5
РЕШЕНИЕ. Нетрудно показать, что первый закон Кирхгофа применим не только к узлу, но и к любому сечению, поэтому
- i1 - i2 + i3 = 0.
Отсюда i3 = i1 + i2 . Затем i5 = i3 + i4 и i6 = - i2 - i4.
Записывая
заданные токи в комплексной форме для
действующих значений
![]() ;
;
![]() ;
;
![]() ;
;
![]() и подставляя их в уравнения, составленные
по первому закону Кирхгофа, находим:
и подставляя их в уравнения, составленные
по первому закону Кирхгофа, находим:
![]() А;
А;
![]() А;
А;
![]() А.
А.
ПРИМЕР 2.5. Определите в комплексной форме действующее значение напряжения ветви по рис. 2.6, если R = 86,5 Ом; XL = 20 Ом;
XC
= 150 Ом;
![]() В;
В;
![]() А.
А.
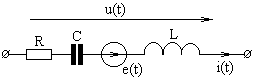
Рис. 2.6
РЕШЕНИЕ. Согласно второму закону Кирхгофа для действующих значений напряжений имеем:
![]()
или
![]() ,
,
где
![]() А;
А;
![]() В.
В.
Подставляя численные значения, получаем:
![]() В.
В.