7. Свойство Архимеда. Плотное множество.
Линейно упорядоченная группа
Пусть 
— линейно
упорядоченная группа (англ.), 
и 
—
положительные элементы
.
Элемент
называется бесконечно
малым по
отношению к элементу
(а
— бесконечно
большим по
отношению к
),
если для любого натурального
имеет
место неравенство
Группа называется архимедовой, если для неё выполнена аксиома Архимеда: в не существует пары элементов , , таких что — бесконечно мал по отношению к .
Упорядоченное поле
Пусть 
— упорядоченное
поле.
Поскольку всякое упорядоченное поле
является линейно упорядоченной группой,
то все вышеприведенные определения
бесконечно малого и бесконечно большого
элементов, а также формулировка аксиомы
Архимеда сохраняют силу. Однако здесь
имеется ряд специфических особенностей,
благодаря которым формулировка аксиомы
Архимеда упрощается.
Пусть 
—
положительные элементы
.
элемент бесконечно мал по отношению к элементу , тогда и только тогда, когда
бесконечно
мал по отношению к 
(такие
элементы называются просто, бесконечно
малыми)элемент бесконечно большой по отношению к элементу , тогда и только тогда, когда бесконечно большой по отношению к (такие элементы называются просто, бесконечно большими)
Бесконечно малые и бесконечно большие элементы объединяются под названием инфинитезимальных элементов.
формулировка аксиомы Архимеда:
Для
всякого элемента
поля
существует
натуральный элемент
,
такой что 
Или, эквивалентная формулировка,
Для
всякого положительного элемента
поля 
существует
натуральный элемент
,
такой что 
Примеры и контрпримеры
Множество действительных чисел
Наиболее известный пример архимедова поля — это множество действительных чисел. Если рассматривать множество действительных чисел как пополнениесовокупности рациональных (например, с помощью дедекиндовых сечений), то свойство Архимеда для действительных чисел вытекает из того, что им обладают рациональные числа. В связи с этим следует отметить, что в одной из систем аксиом действительных чисел, которая была предложена Гильбертом[4], совокупность действительных чисел определяется как максимальное архимедово упорядоченное поле, то есть упорядоченное поле, удовлетворяющее аксиоме Архимеда (то есть не содержащее инфинитезимальных элементов), которое нельзя расширить до большего архимедова упорядоченного поля.
Неархимедово упорядоченное поле
В качестве примера (вернее, контрпримера) упорядоченного поля, для которого не выполнена аксиома Архимеда, рассмотрим совокупность рациональных функций с действительными коэффициентами, то есть функций вида
Относительно
обычных операций сложения и умножения
эта совокупность образует поле.
Введем отношение
порядка на
совокупности рациональных функций
следующим образом. Пусть 
и 
—
две рациональные функции. Мы скажем,
что 
,
если и только если в
некоторой окрестности 
разность 
имеет
строго положительный знак. Это условие
можно сформулировать и в терминах
коэффициентов рациональных функций
и
.
Запишем разность
в
виде многочлен + правильная рациональная
дробь:
где
второе слагаемое в правой части —
правильная рациональная дробь, то есть
степень числителя меньше степени
знаменателя: 
.
Будем также считать что старший
коэффициент знаменателя 
равен 
.
Тогда
тогда
и только тогда, когда либо 
,
либо полиноминальная часть отсутствует
и 
.
Несложно проверить корректность этого
определения порядка (следует проверить
как то, что введенное отношение
действительно является отношением
порядка, и что это отношение согласовано
с операциями поля).
Таким образом, совокупность рациональных функций образует упорядоченное поле. Заметим, что оно является расширением поля действительных чисел, но аксиома Архимеда здесь не имеет места (см. конец предыдущего раздела!). Действительно, рассмотрим элементы и . Очевидно, каким бы ни было натуральное число , имеет место неравенство:
Другими словами, — бесконечно большой элемент поля. Тем самым аксиома Архимеда в этом поле не имеет места.
Пло́тное мно́жество — подмножество пространства, точками которого можно сколь угодно хорошо приблизить любую точку объемлющего пространства.
Определения
Пусть даны топологическое пространство
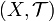и
два подмножества 
Тогда множество
называется плотным
в множестве
,
если любаяокрестность любой
точки
содержит
хотя бы одну точку из
,
то есть
Множество называется всюду плотным, если оно плотно в
