
- •Примеры
- •5. Ограниченное снизу множество. Инфимум множества.
- •7. Свойство Архимеда. Плотное множество.
- •Неархимедово упорядоченное поле
- •8. Единственность поля действительных чисел. Расширенное множество действительных чисел.
- •10. Теорема Больцано – Вейерштрасса.
- •12. Окрестность точки. Внутренняя точка. Открытое и замкнутое множества.
- •13. Проколотая окрестность точки. Открытый и замкнутый интервалы.
- •15. Открытое покрытие. Теорема Гейн-Бореля.
- •Лемма Гейне — Бореля
- •16. Понятие функций. Область определения. Область значения.
- •17. Кольцо функций. Деление двух функций.
- •Примеры
- •Алгоритм Евклида
- •Свойства евклидовых колец
- •Свойства модулей над евклидовым кольцом
- •20. Односторонние пределы функций.
- •21. Пределы функций в бесконечности. Бесконечный предел.
- •22. Монотонная функция.
- •Условия монотонности функции
- •2) В. П. (н. П.) функции f(X) в точке x0 предел верхних (нижних) граней множеств значений функции f(X) в окрестности точки х0, когда эти окрестности стягиваются к точке х0. Он обозначается
- •Непрерывность функции в точке
- •Определение 25 (точки разрыва). A - точка разрыва f, если
- •28. Композиция двух функции и её непрерывность.
- •29. Ограниченная функция. Ограниченность непрерывных функции в замкнутом интервале.
- •Определение
- •37. Дифференцирование сложной функции.
- •38. Односторонние производные функции.
- •39. Экстремумы и точки перегиба функции.
- •Экстремумы
- •В ыпуклость и вогнутость.
- •40. Теорема Ролля.
- •Теорема (Ролля):
- •41. Теорема о промежуточном значении для производной.
- •Отношение бесконечно больших
- •43. Полином Тейлора. Остаточный член.
- •44. Теорема Тейлора.
- •45. Расширенная теорема о главном значении.
Математический анализ 1
1. Свойства операций поля действительных чисел. Пример некоммутативных и не ассоциативных операций.
(А) а+в=в+а, а*в=в*а – коммутативность
(В) (а+в)+с=а+(в+с) - ассоциативность
(С) а*(в+с)=а*в+а*с – дистрибутивность
(D) ᴲ 0,1; 0≠1 » а+0=а и а*1=а – свойство нейтральных элементов.
(Е) для любого а ᴲ -а : а+(-а)=0
а≠0 ᴲ а-1: а* а-1 =1
(F) для любого а, в € R: а=в, а<в, в <а – линейный порядок
(G) а<в и в<с » а<с - свойство транзитивности
(H) а<в для любого с € R
а+с < в+с, 0<с а*с<в*с
[R, (А)-(Е), (F)-(Н)] – упорядоченное поле.
Пример: некоммутативных операций.
4-2=2 ≠ 2-4=-2
4/2=2 ≠ 2/4=½
не ассоциативных операций:
8-(4-2)=6 ≠ (8-4)-2=2
не дистрибутивности:
8/(4-2)=4 ≠ 8/4-8/2=-2
2. Упорядоченность поля действительных чисел. Неупорядоченное поле.
Определение
Пусть ![]() — алгебраическое
поле и
для его элементов определён линейный
порядок,
то есть задано отношение
— алгебраическое
поле и
для его элементов определён линейный
порядок,
то есть задано отношение ![]() (меньше
или равно) со следующими свойствами:
(меньше
или равно) со следующими свойствами:
Рефлексивность:
 .
.Транзитивность: если
 и
и 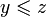 ,
то
,
то 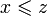 .
.Антисимметричность: если и
 ,
то
,
то 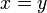 .
.Линейность: все элементы сравнимы между собой, то есть либо
 ,
либо
.
,
либо
.Согласованность со сложением: если , то для любого z:
 .
.Согласованность с умножением: если
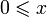 и
и 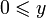 ,
то
,
то 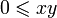 .
.
Связанные определения
Для удобства записи вводятся дополнительные вторичные отношения:
Отношение больше
или равно: ![]() означает,
что
.
означает,
что
.
Отношение больше: ![]() означает,
что
и
означает,
что
и ![]() .
.
Отношение меньше: ![]() означает,
что
означает,
что ![]() .
.
Формула с любым из этих 4 отношений называется неравенством.
Числа, бо́льшие нуля, называются положительными, а меньшие нуля — отрицательными.
Конструктивное построение порядка
Один
из способов определить в поле F линейный
порядок — выделить в нём подмножество
положительных чисел P,
замкнутое относительно сложения и
умножения и обладающее следующим
свойством. три подмножества ![]() ,
ноль и
,
ноль и ![]() не
пересекаются и вместе образуют разбиение
всего поля.
не
пересекаются и вместе образуют разбиение
всего поля.
Пусть
такое P выделено.
Обозначим ![]() (это
множество тоже замкнуто относительно
сложения и умножения) и определим
линейный порядок в Fследующим
образом:
(это
множество тоже замкнуто относительно
сложения и умножения) и определим
линейный порядок в Fследующим
образом:
,
если ![]()
Все приведенные выше аксиомы порядка тогда выполнены.
Некоторые свойства
Всякий элемент упорядоченного поля относится к одной и только одной из трёх категорий: положительные числа, отрицательные числа, нуль. Если
 положителен,
то
положителен,
то  отрицателен,
и наоборот.
отрицателен,
и наоборот.В любом упорядоченном поле
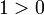 и
квадрат любого ненулевого элемента
положителен.
и
квадрат любого ненулевого элемента
положителен.Однотипные неравенства можно складывать:
Если
и ![]() ,
то
,
то ![]() .
.
Неравенства можно умножать на положительные элементы:
Если
и ![]() ,
то
,
то ![]() .
.
Место в иерархии алгебраических структур
Подполе упорядоченного поля наследует родительский порядок и, следовательно, тоже является упорядоченным полем.
Характеристика упорядоченного поля всегда равна нулю. Поэтому конечное поле не может быть упорядочено.
Поле допускает упорядочение тогда и только тогда, когда
 не
может быть представлена как сумма
квадратов элементов поля. Поэтому
нельзя продолжить вещественный порядок
на комплексные
числа.
не
может быть представлена как сумма
квадратов элементов поля. Поэтому
нельзя продолжить вещественный порядок
на комплексные
числа.Наименьшее упорядоченное поле — это поле рациональных чисел, которое может быть упорядочено только одним способом. Это или изоморфное емурациональное поле содержится как подполе в любом другом упорядоченном поле. Если в поле не существует элемента больше, чем все элементы рационального поля, поле называется архимедовым.
Примеры
Рациональные числа
Вещественные числа
Вещественные алгебраические числа
Поле вещественных рациональных функций:
 ,
где
,
где  — многочлены,
— многочлены, 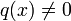 .
Упорядочим его следующим образом.
.
Упорядочим его следующим образом.Вещественные константы (как многочлены нулевого порядка) упорядочены традиционным образом.
Пусть
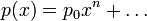 ,
, 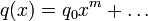 Будем
считать, что дробь
Будем
считать, что дробь 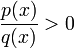 ,
если
,
если 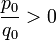 .
.Из определения вытекает, что многочлен
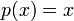 больше,
чем любая константа, то есть аксиома
Архимеда для
этого поля не выполняется, поле
неархимедово.
больше,
чем любая константа, то есть аксиома
Архимеда для
этого поля не выполняется, поле
неархимедово.
Гипервещественные числа — ещё один пример неархимедова поля.
3. Неравенство треугольника, абсолютное значение действительных чисел.
Если а, в € R, то |a+в|≤|а|+|в|
а, в ≥0 » а+в≥0
|a+в|=а+в=|а|+|в|
а, в≤0 » а+в≤0
|a+в|=-(а+в)=-а+(-в)= |а|+|в|
а≤0, в≥0 » а+в= -|а|+|в|
|a+в|=|-|а|+|в|| ≤ |а|+|в|
а≥0, в≤0
|a+в|=|а|-|в|
|a+в|=||а|-|в||≤ |а|+|в|
Следствие: если а, в € R, тогда |а|-|в|≥||а|-|в||
|а|+|в|≥||а|-|в||
Абсолютное
значение
или модуль
действительного числа a
(обозначается как |a|) определяется как
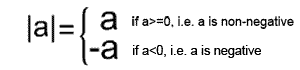
Пример |5|=5 Так как 5>0 |-4/7|= -(-4/7) = 4/7 Так как -4/7<0 |0|=0 Так как 0≥0
Замечание |a| есть не отрицательным числом для всех значений a и -|a|≤ a ≤ |a|
4. Ограниченное сверху множество. Супремум множества.
1)
Точной (наименьшей) верхней гранью
(границей),
или супре́мумом
подмножества
![]() упорядоченного
множества
(или класса)
упорядоченного
множества
(или класса)
![]() ,
называется наименьший элемент
,
который равен или больше всех элементов
множества
.
Другими словами, супремум — это наименьшая
из всех верхних граней. Обозначается
,
называется наименьший элемент
,
который равен или больше всех элементов
множества
.
Другими словами, супремум — это наименьшая
из всех верхних граней. Обозначается
![]() .
.
Более
формально:
![]() —
множество верхних
граней
,
то есть элементов
,
равных или больших всех элементов
—
множество верхних
граней
,
то есть элементов
,
равных или больших всех элементов
![]()
Либо
2) Пусть X – линейно упорядоченное множество с отношением >= и Y ⊆ X.
Элемент m ∈ X называется верхней границей множества Y , если m > y для любого y ∈ Y . Элемент m ∈ X называется точной верхней гранью множества Y , если он является верхней границей этого множества и для любой другой верхней границы m0 выполнено неравенство m0> m. Точная верхняя грань обозначается supY или sup y∈Yy и по другому называется супремумом множества Y .
Примеры
Для множества
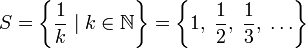
![]() ;
;
![]() .
.
Множество положительных рациональных чисел
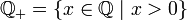 не
имеет точной верхней грани в
не
имеет точной верхней грани в
 ,
точная нижняя грань
,
точная нижняя грань
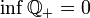 .
.Множество
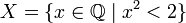 рациональных
чисел, квадрат которых меньше двух, не
имеет точных верхней и нижней граней
в
,
но если его рассматривать как подмножество
множества действительных
чисел,
то
рациональных
чисел, квадрат которых меньше двух, не
имеет точных верхней и нижней граней
в
,
но если его рассматривать как подмножество
множества действительных
чисел,
то
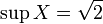 и
и
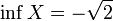
5. Ограниченное снизу множество. Инфимум множества.
Пусть X – линейно упорядоченное множество с отношением >= и Y ⊆ X.
Элемент m ∈ X называется нижней границей множества Y , если y > m для любого y ∈ Y .
Элемент m ∈ X называется точной нижней гранью множества Y , если он является нижней границей этого множества и для любой другой нижней границы m0 выполнено неравенство m > m0. Точная нижняя грань обозначается inf Y или inf y∈Yy и по другому называется инфимумом множества Y .
либо:
Точной
(наибольшей) нижней гранью (границей),
или и́нфимумом
(лат.
infimum
— самый низкий) подмножества
упорядоченного
множества
(или класса)
,
называется наибольший элемент
,
который равен или меньше всех элементов
множества
.
Другими словами, инфимум — это наибольшая
из всех нижних граней. Обозначается
![]() .
.
Примеры
1)На
множестве всех рациональных
чисел,
больших пяти, не существует минимума,
однако существует инфимум.
![]() такого
множества равен пяти. Инфимум не является
минимумом, так как пять не принадлежит
этому множеству. Если же определить
множество всех натуральных чисел,
больших пяти, то у такого множества есть
минимум и он равен шести. Вообще говоря,
у любого непустого подмножества множества
натуральных чисел существует минимум[1].
такого
множества равен пяти. Инфимум не является
минимумом, так как пять не принадлежит
этому множеству. Если же определить
множество всех натуральных чисел,
больших пяти, то у такого множества есть
минимум и он равен шести. Вообще говоря,
у любого непустого подмножества множества
натуральных чисел существует минимум[1].
2)Для множества
; .
3)Множество положительных рациональных чисел не имеет точной верхней грани в , точная нижняя грань .
4)Множество рациональных чисел, квадрат которых меньше двух, не имеет точных верхней и нижней граней в , но если его рассматривать как подмножество множества действительных чисел, то
и
6. Аксиома полноты. Пример неполных множеств.
Аксиома
непрерывности (полноты). Каковы
бы ни были непустые множества ![]() и
и ![]() ,
такие что для любых двух
элементов
,
такие что для любых двух
элементов ![]() и
и ![]() выполняется
неравенство
выполняется
неравенство ![]() ,
существует такое число
,
существует такое число ![]() ,
что для всех
и
имеет
место соотношение
,
что для всех
и
имеет
место соотношение
![]()
Геометрически,
если трактовать действительные числа
как точки
на прямой,
данное утверждение представляется
очевидным. Если два множества ![]() и
и ![]() таковы,
что на числовой прямой все элементы
одного из них лежат левее всех элементов
второго, то найдется число
, разделяющее эти
два множества, то есть лежащее правее
всех элементов
(кроме,
возможно, самого
)
и левее всех элементов
(та
же оговорка).
таковы,
что на числовой прямой все элементы
одного из них лежат левее всех элементов
второго, то найдется число
, разделяющее эти
два множества, то есть лежащее правее
всех элементов
(кроме,
возможно, самого
)
и левее всех элементов
(та
же оговорка).
Здесь следует отметить, что несмотря на «очевидность» данного свойства, для рациональных чисел оно не всегда выполняется. Для примера, рассмотрим два множества:
![]()
Легко
видеть, что для любых элементов
и
выполняется
неравенство ![]() .
Однако рационального числа
,
разделяющего эти два множества, не
существует. В самом деле, этим числом
может быть только
.
Однако рационального числа
,
разделяющего эти два множества, не
существует. В самом деле, этим числом
может быть только ![]() ,
но оно не
является рациональным.
,
но оно не
является рациональным.
Доказательство иррациональности
Применим доказательство
от противного:
допустим,
рационален,
то есть представляется в виде несократимой
дроби ![]() ,
где
,
где ![]() и
и ![]() — целые
числа.
Возведём предполагаемое равенство в
квадрат:
— целые
числа.
Возведём предполагаемое равенство в
квадрат:
![]() .
.
Отсюда
следует, что ![]() чётно,
значит, чётно и
.
Пусть
чётно,
значит, чётно и
.
Пусть ![]() ,
где
,
где ![]() целое.
Тогда
целое.
Тогда
![]()
Следовательно, ![]() чётно,
значит, чётно и
.
Мы получили, что
и
чётны,
что противоречит несократимости дроби
.
Значит, исходное предположение было
неверным, и
—
иррациональное число.
чётно,
значит, чётно и
.
Мы получили, что
и
чётны,
что противоречит несократимости дроби
.
Значит, исходное предположение было
неверным, и
—
иррациональное число.
