
- •Примеры
- •5. Ограниченное снизу множество. Инфимум множества.
- •7. Свойство Архимеда. Плотное множество.
- •Неархимедово упорядоченное поле
- •8. Единственность поля действительных чисел. Расширенное множество действительных чисел.
- •10. Теорема Больцано – Вейерштрасса.
- •12. Окрестность точки. Внутренняя точка. Открытое и замкнутое множества.
- •13. Проколотая окрестность точки. Открытый и замкнутый интервалы.
- •15. Открытое покрытие. Теорема Гейн-Бореля.
- •Лемма Гейне — Бореля
- •16. Понятие функций. Область определения. Область значения.
- •17. Кольцо функций. Деление двух функций.
- •Примеры
- •Алгоритм Евклида
- •Свойства евклидовых колец
- •Свойства модулей над евклидовым кольцом
- •20. Односторонние пределы функций.
- •21. Пределы функций в бесконечности. Бесконечный предел.
- •22. Монотонная функция.
- •Условия монотонности функции
- •2) В. П. (н. П.) функции f(X) в точке x0 предел верхних (нижних) граней множеств значений функции f(X) в окрестности точки х0, когда эти окрестности стягиваются к точке х0. Он обозначается
- •Непрерывность функции в точке
- •Определение 25 (точки разрыва). A - точка разрыва f, если
- •28. Композиция двух функции и её непрерывность.
- •29. Ограниченная функция. Ограниченность непрерывных функции в замкнутом интервале.
- •Определение
- •37. Дифференцирование сложной функции.
- •38. Односторонние производные функции.
- •39. Экстремумы и точки перегиба функции.
- •Экстремумы
- •В ыпуклость и вогнутость.
- •40. Теорема Ролля.
- •Теорема (Ролля):
- •41. Теорема о промежуточном значении для производной.
- •Отношение бесконечно больших
- •43. Полином Тейлора. Остаточный член.
- •44. Теорема Тейлора.
- •45. Расширенная теорема о главном значении.
28. Композиция двух функции и её непрерывность.
Определение
Пусть ![]() и
и ![]() две
функции. Тогда их композицией называется
функция
две
функции. Тогда их композицией называется
функция ![]() ,
определённая равенством:
,
определённая равенством:
![]() .
.
Связанные определения
Термин «сложная функция» может быть применим к композиции двух функций, тем не менее он чаще употребляется в ситуации когда на вход функции нескольких переменных подаётся набор функций от одной или нескольких исходных переменных. Например функция вида
![]()
Свойства композиции
Композиция ассоциативна:
![]() .
.
Если
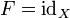 — тождественное
отображение на
,
то есть
— тождественное
отображение на
,
то есть
![]() ,
,
то
![]() .
.
Если
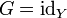 —
тождественное отображение на
—
тождественное отображение на  ,
то есть
,
то есть
![]() ,
,
то
![]() .
.
Рассмотрим пространство всех биекций множества на себя и обозначим его
 .
То есть если
.
То есть если  ,
то
,
то  —
биекция. Тогда композиция функций
из
является бинарной
операцией,
а
—
биекция. Тогда композиция функций
из
является бинарной
операцией,
а  — группой.
— группой.  является нейтральным
элементом этой
группы. Обратным к
элементу
является
является нейтральным
элементом этой
группы. Обратным к
элементу
является  — обратная
функция.
— обратная
функция.Группа , вообще говоря, не коммутативна, то есть
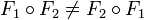 .
.
Дополнительные свойства
Композиция непрерывных функций непрерывна. Пусть
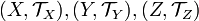 — топологические
пространства.
Пусть
— топологические
пространства.
Пусть  и
и 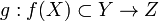 две
функции,
две
функции, 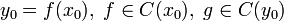 .
Тогда
.
Тогда  .
.
Композиция дифференцируемых функций дифференцируема. Пусть
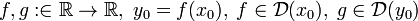 .
Тогда
.
Тогда  ,
и
,
и
![]() .
.
29. Ограниченная функция. Ограниченность непрерывных функции в замкнутом интервале.
Ограниченная функция. Пусть функция (одного или многих переменных) определена на множестве D. Если множество ее значений ограничено, когда аргумент (аргументы) пробегают все множество D, функция называется ограниченной. Соответственно, если множество значений функции ограничено сверху (снизу), то функция также называется ограниченной сверху (снизу).
Пример1.
Рассмотрим функцию ![]() Она
ограничена на луче [1; +) (её модуль на
этом множестве не больше 1), но не
ограничена и не ограничена сверху на
интервале (0; 1), хотя на нём ограничена
снизу (например, числом 1). На луче (–∞;
1) она ограничена (её модуль на этом
множестве также не больше 1), не ограничена
и не ограничена снизу на интервале (–1;
0), хотя на нём она ограничена сверху
(например, числом 0 или числом –1). Все
указанные свойства хорошо видны на
графике функции.
2. Функция z = x2 + y2 ограничена
на любом ограниченном множестве точек
плоскости; на таком множестве она,
естественно, ограничена и сверху, и
снизу.
Она
ограничена на луче [1; +) (её модуль на
этом множестве не больше 1), но не
ограничена и не ограничена сверху на
интервале (0; 1), хотя на нём ограничена
снизу (например, числом 1). На луче (–∞;
1) она ограничена (её модуль на этом
множестве также не больше 1), не ограничена
и не ограничена снизу на интервале (–1;
0), хотя на нём она ограничена сверху
(например, числом 0 или числом –1). Все
указанные свойства хорошо видны на
графике функции.
2. Функция z = x2 + y2 ограничена
на любом ограниченном множестве точек
плоскости; на таком множестве она,
естественно, ограничена и сверху, и
снизу.
Теорема (об
ограниченности непрерывной функции)
Пусть
функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() .
Тогда
.
Тогда ![]() ограничена
на
,
то есть существует такая постоянная
ограничена
на
,
то есть существует такая постоянная ![]() ,
что
,
что ![]() при
всех
при
всех ![]() .
.
Доказательство.
Предположим обратное: пусть
не
ограничена, например, сверху. Тогда все
множества ![]() ,
, ![]() ,
, ![]() ,
не пусты. По предыдущей лемме в каждом
из этих множеств
,
не пусты. По предыдущей лемме в каждом
из этих множеств ![]() имеется
наименьшее значение
имеется
наименьшее значение ![]() ,
, ![]() .
Покажем, что
.
Покажем, что
![]() Действительно,
Действительно, ![]() .
Если какая-либо точка из
.
Если какая-либо точка из ![]() ,
например
,
лежит между
,
например
,
лежит между ![]() и
и ![]() ,
то
,
то
![]() то
есть
то
есть ![]() --
промежуточное значение между
--
промежуточное значение между ![]() и
и ![]() .
Значит, по теореме о промежуточном
значении непрерывной функции, существует
точка
.
Значит, по теореме о промежуточном
значении непрерывной функции, существует
точка ![]() ,
такая что
,
такая что ![]() ,
и
,
и ![]() .
Но
.
Но ![]() ,
вопреки предположению о том, что
--
наименьшее значение из множества
,
вопреки предположению о том, что
--
наименьшее значение из множества ![]() .
Отсюда следует, что
.
Отсюда следует, что ![]() при
всех
при
всех ![]() .
.
Точно
так же далее доказывается, что ![]() при
всех
при
всех ![]() ,
, ![]() при
всех
при
всех ![]() ,
и т. д. Итак,
,
и т. д. Итак, ![]() --
возрастающая последовательность,
ограниченная сверху числом
--
возрастающая последовательность,
ограниченная сверху числом ![]() .
Поэтому существует
.
Поэтому существует ![]() .
Из непрерывности функции
следует,
что существует
.
Из непрерывности функции
следует,
что существует ![]() ,
но
,
но ![]() при
при ![]() ,
так что предела не существует. Полученное
противоречие доказывает, что
функция
ограничена
сверху.
,
так что предела не существует. Полученное
противоречие доказывает, что
функция
ограничена
сверху.
Аналогично доказывается, что ограничена снизу, откуда следует утверждение теоремы.
30. Теорема о промежуточном значении.
Теорема
(о промежуточном значении).
Пусть функция
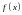 непрерывна на отрезке
непрерывна на отрезке
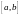 и
и
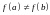 .
.
Тогда
каждое число
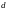 ,
принадлежащее интервалу с концами в
точках
,
принадлежащее интервалу с концами в
точках
 и
и
 является значением функции хотя бы в
одной точке
является значением функции хотя бы в
одной точке
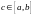 ,
то есть
,
то есть
 .
.
Доказательство.
►Рассмотрим функцию
 .
Очевидно, что
.
Очевидно, что
 и
и
 непрерывна на
.
Тогда по предыдущей теореме существует
точка
непрерывна на
.
Тогда по предыдущей теореме существует
точка
 ,
откуда получаем
.◄
,
откуда получаем
.◄
Замечание. Требование непрерывности функции в последних теоремах существенно.
Примером,
иллюстрирующим этот факт, может служить
функция
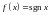 ,
определенная на отрезке
,
определенная на отрезке
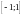 и не принимающая значения
и не принимающая значения
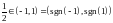 .
.
31. Равномерная непрерывность функции. Примеры. Теорема.
О
п р е д е л е н и е 1. Функция ![]() ,
определенная на множестве
,
определенная на множестве ![]() ,
называется равномерно непрерывной на
этом множестве, если для всякого
,
называется равномерно непрерывной на
этом множестве, если для всякого ![]() найдется
найдется ![]() ,
зависящее только от
,
зависящее только от ![]() ,
такое, что
,
такое, что
![]()
для
всех ![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ![]() .
.
Т
е о р е м а 1. Если функция ![]() определена
и непрерывна на отрезке
определена
и непрерывна на отрезке ![]() ,
то она равномерно непрерывна на нем.
,
то она равномерно непрерывна на нем.
Д
о к а з а т е л ь с т в о. Допустим, что
теорема неверна. Тогда существует
такое ![]() ,
что для любого
найдется
пара точек
,
что для любого
найдется
пара точек ![]() ,
удовлетворяющих неравенству
,
для которых
,
удовлетворяющих неравенству
,
для которых
![]() .
.
Зададим
стремящуюся к нулю последовательность
положительных чисел ![]() .
Для каждого
.
Для каждого ![]() найдутся
точки
найдутся
точки ![]() такие,
что
такие,
что
![]() ,
но
,
но ![]() .
(1)
.
(1)
Так
как последовательности ![]() принадлежат
к
,
то эта последовательность ограничена
и из нее по теореме Больцано-Вейерштрасса
можно выделить подпоследовательность
принадлежат
к
,
то эта последовательность ограничена
и из нее по теореме Больцано-Вейерштрасса
можно выделить подпоследовательность ![]() ,
сходящуюся к некоторой точке
,
сходящуюся к некоторой точке ![]() .
Так как
.
Так как ![]() ,
, ![]() ,
то подпоследовательность
,
то подпоследовательность ![]() тоже
сходится к точке
тоже
сходится к точке ![]() .
По условию функция
непрерывна
на
.
По условию функция
непрерывна
на ![]() и,
следовательно, непрерывна в точке
.
Конечно, если
и,
следовательно, непрерывна в точке
.
Конечно, если ![]() или
или ![]() ,
то надо считать, что
непрерывна
в
справа
или соответственно слева. Поэтому
,
то надо считать, что
непрерывна
в
справа
или соответственно слева. Поэтому
![]() .
.
После перехода к пределу в (1) при получим
![]() ,
(2)
,
(2)
и
мы пришли к противоречию: ![]() .
.
Заметим, что в (2) мы воспользовались непрерывностью функции Теорема доказана.
П р и м е р 1. Функция
![]()
непрерывна
на отрезке ![]() ,
поэтому на основании теоремы 1 она
равномерно непрерывна на этом отрезке.
,
поэтому на основании теоремы 1 она
равномерно непрерывна на этом отрезке.
С
другой стороны, на полуинтервале ![]() эта
функция хотя и непрерывна, но не является
равномерно непрерывной. Это показывает,
что требование в теореме 1, чтобы
непрерывная функция была задана на
отрезке, а не на интервале, существенно.
эта
функция хотя и непрерывна, но не является
равномерно непрерывной. Это показывает,
что требование в теореме 1, чтобы
непрерывная функция была задана на
отрезке, а не на интервале, существенно.
Убедимся
в том, что наша функция не является
равномерно непрерывной на
.
Точки ![]() ,
очевидно, принадлежат полуинтервалу
,
и для них
,
очевидно, принадлежат полуинтервалу
,
и для них
 .
.
Если
задать ![]() ,
то при любом
найдется
такое
,
то при любом
найдется
такое ![]() ,
что
,
что
![]() ,
,
между тем как
![]() .
.
Из
сказанного следует, что нашу функцию
нельзя продолжить на отрезок ![]() ,
доопределив ее в точке
,
доопределив ее в точке ![]() так,
чтобы она стала непрерывной на
,
потому что тогда, согласно теореме 1,
она была бы равномерно непрерывной
на
,
а следовательно, и на
,
чего быть не может.
так,
чтобы она стала непрерывной на
,
потому что тогда, согласно теореме 1,
она была бы равномерно непрерывной
на
,
а следовательно, и на
,
чего быть не может.
32. Непрерывность непостоянной монотонной функции на отрезках.
33. Дифференцируемость функции во внутренней точке.
34. Различные интерпретации производной функции.
35. Дифференцируемость и непрерывность.
36. Дифференцирование и арифметические операций.
