2) В. П. (н. П.) функции f(X) в точке x0 предел верхних (нижних) граней множеств значений функции f(X) в окрестности точки х0, когда эти окрестности стягиваются к точке х0. Он обозначается

Пусть функция f(x) определена на метрич. пространстве R и принимает действительные значения на R. Если x₀ ∈ R и О(х₀; ε) есть ε-окрестность точки х₀, ε > 0, то

соответственно

В каждой точке x ∈ R у функции f(x) существуют как в. п. f̄(x), так и н. п. f̠(x) (конечные или бесконечные). Функция f̄(x) полунепрерывна сверху, а функция f̠(x) полунепрерывна снизу на пространстве R (в смысле понятия полунепрерывности функций, принимающих значения из расширенной числовой прямой).

Для того чтобы функция f(x) в точке х₀ имела предел (конечный или бесконечный, равный одному из символов +∞ или -∞), необходимо и достаточно, чтобы

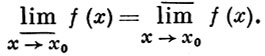
Естественным образом понятие в. п. (н. п.) функции в точке переносится на действительные функции, определенные на топологич. пространствах.

3) В. п. (н. н.) последовательности множеств А_n, n = 1, 2, ... , множество

состоящее из таких элементов х, к-рые принадлежат бесконечному числу множеств А_n; соответственно, множество

таких элементов х, к-рые принадлежат всем множествам А_n, начиная с нек-рого номера n = n(х). Очевидно, А̠ ⊂ А̄.

24. Непрерывность функций. Первая и левая непрерывность.

Непрерывность функции в точке

Пусть f:E® R, a -точка области определения.

Определение 21 (непрерывность функции в точке). Функция  f(x) называется непрерывной в точке a, если

" U(f(a)) $ U(a) (f(U(a))М U(f(a))).

Дадим определение непрерывной функции в точке на "языке e–d " (ср. с определением предела по Коши.)

Определение 22 (непрерывность функции по Коши). Функция f(x) называется непрерывной в точке a, если " e > 0 $ d(e)>0: " x удовлетворяющих условию |x-a|< d, выполнено неравенство |f(x)-f(a)|< e

Замечание. Если a – изолированная точка множества E, то есть точка, что в некоторой окрестности этой точки нет других точек множества E, кроме точки a, то U(a) = a. Следовательно, f(U(a)) = f(a)М U(f(a)), " U(f(a)). Таким образом, в любой изолированной точке функция непрерывна. Поэтому содержательная часть понятия непрерывности относится к случаю, когда a- предельная точка множества E.

Из определения непрерывной функции следует, что

f:E® R непрерывна в aО E, где a- предельная точка EЫ Ы lim_x® af(x) = f(a)

Последнее равенство можно переписать в следующей форме

lim_x® af(x) = f(lim_x® ax),

которое говорит о том, что непрерывные в точке функции перестановочны с операцией предельного перехода.

Определение 25 (точки разрыва). A - точка разрыва f, если

$ e>0 " d(e)>0 $ xО E : |x-a|<d Ю |f(x)-f(a)|>e.

Различают точки разрыва первого рода (когда существуют конечные односторонние пределы функции слева и справа при x® a, не равные друг другу) и второго рода (когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует). Так в примере на рис. 15 x = 0 является точкой разрыва первого рода. К точкам разрыва первого рода относятся точкиустранимого разрыва, когда предел функции при x® a существует, но в точке aфункция либо неопределена, либо f(a)№ lim x® af(x).

Пример 23.

f(x) =

м sin x/x, если x№ 0 н о 0, если x = 0.

Так как lim_x® asin x/x = 1, то x = 0 является точкой устранимого разрыва.

Пример 24. Функция Дирихле разрывна во всех точках и все точки разрыва второго рода, так как на любом интервале есть рациональные и иррациональные числа.

Свойства функций, непрерывных в точке

Отметим основные локальные свойства непрерывных функций.

Теорема 9 (локальные свойства непрерывных функций).

1. Пусть функция f:E® R непрерывна в точке a. Тогда f(x) ограничена в некоторой окрестности точки a.

2. Пусть функция f(x) непрерывна в точке a и f(a)№ 0, то в некоторой окрестности точки a все значения функции положительны или отрицательны вместе с f(a).

3. Если f(x), g(x) - непрерывны в точке a, то функции: f(x)+g(x), f(x)g(x), f(x)/g(x) (при g(a)№ 0 ) непрерывны в точке a.

4. Если функция g(x):Y® R непрерывна в точке bО Y, а функция f:E® Y непрерывна в точке a, f(a) = b, тогда композиция g_° f также непрерывна в точке a.

Данная теорема следует из определения непрерывности функции и соответствующих свойств предела функции.

Глобальные свойства непрерывных функций

Определение 26 (непрерывность функции на множестве).  Функция называется непрерывной на множестве, если она непрерывна в каждой точке множества.

То, что f(x) непрерывна на множестве X обозначается следующим образом: f(x)ОC_X.

Определение 27. Функция называется непрерывной на отрезке [a,b] , если она непрерывна в каждой внутренней точке этого отрезка и непрерывна справа в точке a и непрерывна слева в точке b.

То, что f(x) непрерывна на отрезке [a,b] обозначается следующим образом: f(x)ОC_[a,b].

Перечислим основные глобальные свойства непрерывных функций.

Теорема 10 (глобальные свойства непрерывных функций).

1. (Первая теорема Вейерштрасса) Если функция f(x)О C_[a,b], то онаограничена на [a,b] (см. рис. 18).

2. (Вторая теорема Вейерштрасса) Если f(x)О C_[a,b], то она достигает на [a,b] своих точных верхней и нижней граней (рис. 19)

3. (Теорема Коши) Если f(x)О C_[a,b] и f(a)f(b)<0, то существует cО [a,b] f(c) =0 (см.рис. 20).

Замечание.

1. Функции, не являющиеся непрерывными на данном отрезке, могут принимать точную верхнюю и точную нижнюю грани, например функция Дирихле.

2. Если в условиях теоремы отрезок заменить на интервал, то теорема будет неверна, например, функция 1/x на интервале (0,1) непрерывна, но не является ограниченной; функция y = x на интервале (0,1) не достигает своих точных граней.

25. Непрерывность функций на языке «ɛ-σ».

Определение (непрерывность "на языке приращений").  Функция называется непрерывной в точке a, если выполнено условие

lim_D x® 0D y = 0,

где D y = f(a+D x)-f(a).

Пример 20. Функция f(x) = sin x непрерывна на R. Действительно,

|sin x-sin a| = 2|cos((x+a)/2)sin ((x-a)/2)|Ј 2|sin((x-a)/2)|Ј Ј |x-a|/2 = |x-a|<e,

как только |x-a|<d =e.

Пример 21. Любая последовательность f:N® R есть функция, непрерывная на множестве N, так как каждая точка множества N является его изолированной точкой.

Точки разрыва

Пример 22. Исследовать на непрерывность

f(x) =

м x+1, если xі 0 н о x-1, если x<0.

(рис. 17)

По графику видно, что функция не является непрерывной в точке x = 0. Существуют односторонние пределы функции справа и слева в точке x = 0, которые не равны lim_x® -0f(x) = -1 и lim_x® +0f(x) = 1. То есть определение непрерывной функции в точке не выполнено и точка x = 0 - точка разрыва функции.

Определение 24. Точка a называется точкой разрыва функции f(x), если эта функция не является непрерывной в данной точке.

26. Кусочно-непрерывная функция. Скачок функции.

Теорема (о непрерывности сложной функции). Пусть функция   непрерывна в точке  , а функция   непрерывна в точке  . Тогда сложная функция непрерывна в точке  .

Всевозможные арифметические комбинации простейших элементарных функций, которые рассматривают в школьном курсе алгебры и начал анализа, мы будем называть элементарными функциями. Например,  является элементарной.

Все элементарные функции непрерывны в области определения. Так что   всюду непрерывна, так как всюду определена, а функция   разрывна в точке  .

Дадим теперь классификацию точек разрыва функции. Возможны следующие случаи.

1. Если   и  существуют и конечны, но не равны друг другу, то точку  называют точкой разрыва первого рода. При этом величину  называют скачком функции в точке  .

Пример 20. Исследовать на непрерывность функцию

Решение. Эта функция может претерпевать разрыв только в точке  , где происходит переход от одного аналитического выражения к другому, а в остальных точках области определения функция непрерывна.

Найдем левосторонний предел функции при  . Cлева от точки  , т.е. при  , а  .

Справа от точки    . Тогда  . Значение функции в точке  , т.е.  . Функция в точке  имеет разрыв первого рода. Это видно и на графике функции (рис. 25).

 

 

Рис. 25

 

2. Если в точке    , но в точке   функция   либо не определена, либо  , то точка   является точкой устранимого разрыва.

Последнее объясняется тем, что если в этом случае доопределить или видоизменить функцию  , положив  , то получится непрерывная в точке   функция.

27. Устранимый разрыв функций. Примеры.

Устранимые точки разрыва

Если предел функции существует, но он не совпадает со значением функции в данной точке:

тогда точка   называется точкой устранимого разрыва функции   (в комплексном анализе — устранимая особая точка).

Если «поправить» функцию   в точке устранимого разрыва и положить  , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением фукции до непрерывной илидоопределением фукции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.

Точки разрыва первого и второго рода

Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:

• если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;

• если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода

Пример

Найти точки разрыва функции  , если они существуют. Решение. Данная функция существует при всех значениях x, однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем "поведение" этой функции вблизи точки x = 0, где ее аналитическое выражение изменяется.  Вычислим односторонние пределеы при x = 0.        Следовательно, функция имеет точку разрыва первого рода при x = 0. Скачок функции в этой точке равен        При всех других значениях x функция является непрерывной, поскольку обе составляющие функции слева и справа от точки x = 0 представляют собой элементарные функции без точек разрыва.