В. И. Герчиков взаимное ориентирование социологических шкал

Потребность в методах ранжирования шкал качественных признаков объясняется тем, что, с одной стороны, большинство признаков социальных объектов могут быть адекватно измерены лишь с помощью номинальных шкал, фиксирующих лишь отличие одной позиции от другой. С другой стороны, существующие методы математической обработки данных, полученных анкетированием или опросом, применимы в большинстве случаев к метрическим или порядковым (ранговым) шкалах.

37

Ориентирование шкал является обратной задачей по сравнению с задачей выявления связей. Здесь целью является не получение численной оценки связи между двумя шкалами, а получение такого порядка одной из окал, который максимизировал бы величину коэффициента связи при заданном порядке второй шкалы –базовой.

Необходимые определения

Длиной шкалы признака S назовем число делений шкалы ns. Под направлением шкалы мы понимаем некоторый порядок её значений. Таким образом, шкала S может иметь ns! Направлений. Выделим из этой совокупности два направления – строго по возрастанию и строго по убыванию значений – и назовем их соответственно прямым и обратным.

Ниже будет дан способ вычисления коэффициента  соответствия направлений шкал ориентируемого и базового признаков. Соответствие направлений шкал признаков^ S и q назовем положительным, если оно указывает на одинаковую направленность шкал, и – отрицательным, если оно указывает на противоположную их направленность.

Под ориентированием шкалы S по шкале q мы будем теперь понимать установление такого порядка значений шкалы S, который дает максимум коэффициенту соответствия  направлений шкал этих признаков.

Вычисление коэффициента соответствия

Итак, исследуется соответствие двух фиксированных направлений шкал признаков S и q. Условимся, nsnq. В распоряжении социолога имеется выборка N пар чисел (i, j) первое из которых указывает значение S – того признака, второе – q – того признака для k – того члена иссле

38

дуемой социальной группы или k –того измерения значений признаков исследуемого объекта.

Для характеристики соответствия направлений шкал предлагается следующий метод, аналогичный методам, применяемым в теории обучения и при математическом моделировании психических явлений. Просматривая последовательно выборку N, будем накапливать характеристическое число  увеличивая его при просмотре k –того элемента на некоторую величину _sq^(k)

Величина _sq^(k) показывает, какую информацию о соответствии направлений шкал несет на себе k–тая пара выборки. По просчете всей выборки результирующее характеристическое число нормируется делением на величину выборки – N и на максимальное значение  _sq –.

Итак, для коэффициента соответствия  предлагается следующая формула:

^(k)_sq (1)

Задача, следовательно, сводится к определению формулы для приращения . Для этого подробнее рассмотрим связь направлений шкал двух признаков на примере. Пусть n_s =7, n_q =5. Поместим шкалы одну под другой, причем "вытянем" (см.рис.1) меньшую до размеров большей. При растяжении между элементами меньшей шкалы образуются "промежутки" длиной

(2)

В нашем примере r = 1/2 . Для удобства здесь же нарисуем эти шкалы в обратном порядке.

1	2	3	4	5	6	7
1	2	3		4		5
7	6	5	4	3	2	1
5	4	3		2		1

Рис.1.

39

Пусть признаки S и q принимают значения I и I.

Эта пара, так же, как и пара (7,5), свидетельствует о наличии положительной связи, причем обе пары свидетельствуют об этом

в равной мере. Пары (7,1) или (1,5)свидетельствуют об отрицательной связи направлений шкал. Появление пар (1,2) или (2,2) также свидетельствует о наличии положительной связи, но в меньшей степени, чем пара (I,I). Пары (1,3), (2,3),..., (7,3), (Ф,I), (Ф,2). .., , (Ф,5) не несут, очевидно, никакой информации о связи направлений, так как в эти пары входят средние числа шкал, и, следовательно, они в равной мере могут свидетельствовать как об одинаковой, так и о противоположной направленности шкал.

В соответствии со сказанным мы должны при появлении пары ( i , j ) присвоить положительное значение, если i и j расположены в одноименных половинах шкал S и q, отрицательное значение, если i и j расположены в разных половинах шкал, и нулевое значение, если i или j суть середина соответствующей шкалы. Кроме того, должно быть тем большим по модулю, чем больше соответствующие i и j характеризуют относительность шкал.

Обозначим:

- расстояние между положением i -го значения шкалы S

при прямом и обратном её направлении;

- то же для j -го значения на шкале q.

минимальную из этих величин и предлагается принять в качестве величины приращения коэффициента соответствия направлений при появлении в выборке пары ( i , j ).

Для расстояний ( см. рис. 1) мы получаем следующие формулы:

(3)

(4)

И тогда

если i и j из одноименных половин шкал;

 если i и j из разных половин шкал; (5)

40

формализация условий в (5) приведет нас к формулам:

(6)

(7)

при (8)

Их мы и примем в качестве определения . Шкала для рассматриваемого примера приведена в табл. I.

Таблица I

		i
		1	2	3	4	5	6	7
j	1	6	4	2	0	-2	-4	-6
	2	3	3	2	0	-2	-3	-3
	3	0	0	0	0	0	0	0
	4	-3	-3	-2	0	2	3	3
	5	-6	-4	-2	0	2	4	2

Очевидно, что В итоге

(9)

Из изложенного становится ясно, что по знаку и величине коэффициента соответствия мы можем судить о связи направлений

41

исследуемых шкал. Если , соответствие положительное; если — отрицательное. Чем больше , тем больше соответствие данных направлений шкал исследуемой пары признаков.

Ориентирование. Как явствует из определение процесса ориентирования, мы должны найти такую перестановку значений ориентируемой шкалы, которая дает максимум коэффициенту . Так как число возможных перестановок множества из n элементов равно n! и очень быстро растет с увеличением n , непосредственное применение предложенного метода громоздко:

требуется или переборов.

Для уменьшения необходимой работы предлагается следующий способ. Пусть, например, мы ориентируем шкалу S по шкале q. Разобьем множество данных N на подмножества

тех элементов выборки, в которых признак S принимает значение i. Возьмем множество и просчитаем раз коэффициент , считая последовательно первое деление шкалы S первым, вторым, ... , -тым, Коэффициент каждый раз показывает, какую часть интегрального коэффициента связи несет на себе первый элемент шкалы S в данной перестановке.

Берем теперь множество и проделываем всю работу, перемещая второй элемент по шкале до . Получим таблицу коэффициентов для всех элементов i шкалы S и для всех их положений на шкале. Из этих элементов составляем такую перестановку шкалы S, при которой суммарный коэффициент соответствия максимален. Объем необходимой работы составляет уже не циклов, а лишь , а чаще 2n –3n.

Пример. Ориентирование шкалы S длиной 5 по шкале длиной 4.

Пусть N =25, (здесь , как и , обозначает одновременно как подмножества, так и числа их элементов). Пусть N представлено таблицей 2.

42

Таблица 2

N	1	2	3	4	5	6	7	8	9	10
S	1	1	1	1	1	2	2	2	2	2
q	1	2	2	4	2	2	3	3	3	1

N	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
S	3	3	3	3	3	4	4	4	4	5	5	5	5	5	5
q	2	3	2	3	2	4	4	3	3	4	2	2	2	1	2

имеет следующий вид.

Таблица 3

		i
		1	2	3	4	5
j	1	4	2	0	-2	-4
	2	4/3	4/3	0	-4/3	-4/3
	3	-4/3	-4/3	0	4/3	4/3
	4	-4	-2	0	2	4

Результаты вычисления показаны в табл. 4.

Таблица 4

		i
		1	2	3	4	5
j	1	0.040	-0.013	0.013	-1.147	0.093
	2	0.040	-0.007	0.013	-0.087	0.073
	3	0	0	0	0	0
	4	-0.040	0.007	-0.013	0.087	-0.073
	5	-0.040	0.013	-0.013	0.147	-0.093

43

Из таблицы 4 видно, что наибольшую долю в суммарном коэффициенте соответствия дает четвертое деление шкалы S, если в результирующей перестановке оно станет пятым. Аналогично для пятого деления лучшим положением в результирующей перестановке после фиксации места четвертого деления является первое место шкалы; для второго деления - четвертое (пятое место уке занято); для первого деления - второе место; для третьего остается третье место. Итак, результирующая перестановка шкалы S по шкале q принимает вид 5, I, 3, 2, 4. Коэффициент соответствия для неё

= 0,093 + 0,040 + 0,007 + 0,I47 = 0,287.

Мы видим, что и при такой ориентировке связь признаков S и q остается слабой в рамках данной выборки N.

Программа ориентирования реализует алгоритм относительного ориентирования n шкал различных признаков по шкале одного из них, базового: . Точнее, программа реализует лишь первую часть алгоритма - определение коэффициентов .

Второй этап процесса - выбор перестановки шкалы, дающей максимум результирующему коэффициенту соответствия, выполняется вручную.

Исходные данные вводятся двумя массивами.

Массив А - константы:

- — длина икал рассматриваемых признаков (все )

Шкалы занумерованы по убыванию длин.

- величина выборки N.

- количество рассматриваемых признаков - n.

Если n<9 оставшиеся .

— номер базового признака.

массив В - выборка.

44

Её элементы – целые числа из десятичных цифр.

На S-том месте справа стоит значение S –того признака.

Работа программы. Блок-схема программы представлена на рис. 2.

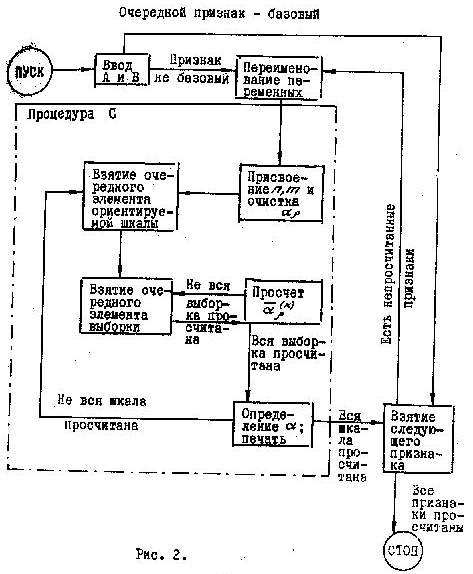
После ввода исходных данных берется первый признак и, если он не базовый, начинается процесс его ориентирования (процедура С). В противном случае берется следующий признак. При просчете каждого следующего признака он обозначается символом S , если его номер меньше номера базового признака, и символом q, если - больше. Соответственно базовый признак получает обозначение q или s .

Процесс ориентирования (работа процедуры С) начинается с замещения символов l, u, v, f символами i, , j, n или j, i, , m. Далее очищаются ячейки , где — номер места, занимаемого перемещаешься делением шкалы ориентируемого признака. Берется очередное деление ориентируемой шкалы ( цикл по l ) и вызывается очередной элемент выборки ( цикл по k ). Определяется значение сравниваемых признаков на данном элементе выборки и по известным формулам подсчитывается приращение , после чего соответствующий коэффициент увеличивается на .

После перебора всей выборки коэффициенты нормируются и на печать выдается номер ориентируемого признака, номер перемещаемого деления шкалы, коэффициенты , соответствующие положению этого деления на -м месте. Затем программа переходит к ориентировке следующего признака. После ориентирования последнего из заданной совокупности признаков программа прекращает работу. На печать, таким образом, выдается массивов по + 2 кодов каждый.

Программа

Begin integer array

Begin integer array

Integer

Procedure c(l,u,v,f);

Begin real array real

Integer k,b,m,n,t;

46

for step 1 until A[1] do

for step 2 until f do

begin for k:=1 step 1 until A[10] do

begin b:=B[k];

u:=entier (b/10 (s-1))-10x entier (b/10 s);

v:=entier (b/10 (q-1))-10x entier (b/10 q);

t:=n+1-2xi; :=(m+1-2xj)x(n-1)/(m-1);

:=if abc(t) abc( ) then abc(t) else

abc( ); if tx <0 then ;

p 1041 (a,l, )

end по l ; go to L2

47

end описаний процедуры;

p 0042(B); a=1;

L : go to if a L A[12] then L 1 else if a=A[12]

Then L 2 3;

L 1 S:=a; q:=A[12]; c(I, ,j,n);

L 2 :s:=A[12]; q:=a; c(j,I, ,m);

L 3 :a:=a=a+1; if a A[11] go to L

End операций,

End программы.

Отладочный пример.

Исходные данные:

Счет (ограничимся ориентированием только первого признака):

a=1; управление передается на L 1;

S=1; q=3; производится замена l на I, uна ,

v на j, f на n;

48

n=3; m=2;

I=1; k=1; b=2113; j=2; t=2;

k=2; b=121;

печать: 1, 1,

I=2; k=1; b=213;

k=2; b=121;

печатать: 1, 2, 0, 0, 0;

I=3; k=1; b=213;

k=2; b=121;

печать: 1, 3, - 0,

Конец ориентирования первого признака.

49

Получили таблицу

Таблица 5

		I
		1	2	3
p	1	0.5	0	-0.5
	2	0	0	0
	3	-0.5	0	0.5

Прямой порядок шкалы (I,2,3) дает наибольший коэффициент при данной выборке =1.

Выводы. Нами описан алгоритм и реализующая его программа ориентирования различных социологических шкал. Мы молем теперь в рамках данной социологической задачи установить, как долина быть построена шкала одного из признаков в зависимости от имеющейся выборки и шкалы другого признака. Более того, этот метод даст нам возможность пользоваться результатами различных социологических исследований. Для этого надо взять совпадающие шкалы за базовые, а шкалы остальных признаков ориентировать по ним.

Подчеркиваем, что все эти выводы можно делать лишь с той степенью точности, с какой отражает реальное положение дел имеющаяся в распоряжении социолога выборка N. В этой связи возникают задачи оценки величины требуемой выборки, точности измерений, надежности результатов применительно к излагаемым методам.

50

Б. Г. Миркин

НОВЫЙ ПОДХОД К ОБРАБОТКЕ СОЦИОЛОГИЧЕСКОЙ ИНФОРМАЦИИ

Данные социологического обследования можно представить следующим образом.

Имеется конечное множество объектов

причем каждый объект характеризуется значениями признаков . Например, признаками могут быть возраст, пол, профессия, удовлетворенность своей работой и т. д.

Предполагается, что каждый признак может принимать значений: Таким образом, каждый объект характеризуется упорядоченным набором

где - значение признака соответствующее объекту . Например, если - профессия, - пол, - возраст, то некоторый объект может характеризоваться набором: (токарь, женский, 26 лет).

Каждый признак порождает разбиение множества n на классов, в один из которых входят объекты с во второй – объекты с и так далее, а последний класс состоит из объектов , таких, что Это разбиение будем обозначать

Полезно различать следующие типы признаков.

Признак p называется количественным, если его значения-

51

ми , являются числа. Таковы, например, возраст, зарплата и т.д.

Признак p называется качественным, если его значения не являются числами, но характеризуют различную степень проявления этого признака, так что между ними имеется естественное упорядочение по степени проявления признака. Качественными признаками являются, например, квалификация ( от "низкой" до "высокой"), удовлетворенность своей работой ( от "очень нравится" до "очень не нравится").

Признак p относится к классификационным, если его значения не являются числами и не связаны естественным упорядочением. К классификационным признакам можно отнести пол, профессию, причину отъезда из данного города и т.д.

Существующие методы обработки данных социологического обследования связаны в основном с обработкой количественных признаков. Качественные признаки обычно при обработке сводят

к количественным (иногда неявно), приписывая их значениям баллы, и применяют далее статистические методы. Например, коэффициент ранговой корреляции для качественных признаков является обычным коэффициентом корреляции для числовых признаков, полученных приписыванием соответствующих баллов значениям данных качественных признаков.

Статистическая обработка таких балльных признаков (например, подсчет среднего значения, дисперсии и т.д.) встречает сильные возражения, поскольку приписанные баллы, вообще говоря, характеризуют лишь упорядочение значений признака, и применение к ним арифметических операций требует обоснования в каждом конкретном случае. Исследование вопросов, связанных с таким обоснованием, потребовало пересмотра и значительного углубления концепции измерения. Полученные к 1963 г. результаты были подытожены в переведенном на русский язык сборнике[2], из которого видно, что разработка обоснования находится пока в зачаточной стадии.

Еще более неясны вопросы, связанные с обработкой классификационных признаков. Иногда значения классификационного признака предварительно упорядочивают ( приписывая баллы) в соответствии с какой-либо содержательной гипотезой (например, по их частости) или мнениями экспертов. В некоторых случаях рас-

52

сматривают статистические показатели, которые имеют смысл и для классификационных признаков (например, мода или энтропия распределения). Иногда, основываясь на эвристических соображениях вводят специальные показатели. Например, наиболее употребительными показателями связи классификационных признаков являются коэффициенты Пирсона и Чупрова [1], которые, по существу, оценивают статистическую значимость отличия n-мерного эмпирического распределения от теоретического равномерного. Предполагается, что, чем более эмпирическое распределение отличается от равномерного, тем теснее связаны признаки. В основе этих коэффициентов лежит подсчет величины , а эта величина указывает лишь на значимость отличия эмпирического распределения от теоретического, но не степень этого отличия.

Таких эвристических показателей можно ввести много, а какой предпочесть — неясно.

Таким образом, существующие методы обработки данных ориентированы в основном на количественные признаки. Это заставляет исследователя для комплексной обработки данных использовать количественные или балльные, качественные признаки.

Между тем классификационные признаки играют существенную роль в характеристике социологических объектов. Поэтому представляет интерес разработка специального аппарата для обработки классификационных признаков. Такой аппарат должен решать широкий круг задач с единой точки зрения.

Заметим, что при обработке данных в терминах классификационных признаков потребуется иногда для единообразия результатов рассматривать количественные и качественные признаки как классификационные (аналогично тому, как теперь часто сводят к количественным признаки других типов). При этом часть информации будет теряться. Однако, поскольку количество значений признаков социологических объектов, как правило, несравнимо меньше объема N обследованных объектов, основная информация о признаках содержится в соответствующих им разбиениях и теряемая информация невелика. В то же время существующие методы обработки, сводящие признаки к количественным, привлекают дополнительную информацию о неколичественных признаках, истинность которой, как правило, очень мало обоснована.

53

Далее мы рассмотрим возможный путь создания аппарата обработки классификационных признаков, дающего единообразные методы решения широкого круга задач.

Информация о классификационном признаке p, собранная

при обследовании множества n, задается разбиением на классы объектов, отвечающих одним и тем же значениям признака. Поэтому вопрос об изучении признаков сводится к изучению соответствующих разбиений.

Мы считаем, что основным инструментом при обработке классификационных признаков должна служить количественная мера близости разбиений данного множества n. Меру близости разбиений обозначим и потребуем, чтобы она удовлетворяла некоторым условиям.

Одно из этих условий состоит в том, чтобы обладала основными свойствами геометрического расстояния. Это требование обусловлено потребностями дальнейшей обработки величин , поскольку применение математического аппарата наиболее эффективно и естественно для мер, удовлетворяющих свойствам геометрического расстояния. Можно возразить, что такое условие не связано с внутренними свойствами признаков объектов и, возможно, в некоторых случаях противоречит им. Однако обнаружение такого противоречия априори невозможно, оно связано именно с практическим применением "геометрических" мер и само по себе явится важным результатом. Пока же соображения удобства обработки являются решающими.

Приведем точную формулировку первого условия.

Аксиома I . Мера обладает следующими свойствами геометрического расстояния:

а) и =0 тогда, когда ( т.е. классы совпадают с классами );

б) = ;

в) для любых разбиений

причем точное равенство достигается, только если разбиение ле-

54

жит между разбиениями и ¹⁾ [3].

Следующая аксиома продиктована требованием равноправия всех объектов , независимо от их конкретных особенностей относительно меры .

Аксиома 2. Если разбиение получено из разбиения перестановкой некоторых объектов, а разбиение - из той же самой перестановкой, то

Потребуем теперь, чтобы при частичном совпадении разбиений и , расстояние между ними можно было вычислить, используя лишь те их классы, на которых они не совпадают.

Аксиома 3. Если разбиения и совпадают всюду, за исключением множества , являющегося сегментом²⁾ их обоих, то вычисляется так, как если бы рассматривались разбиения лишь на множестве Е.

Последняя аксиома дает масштаб измерения.

Аксиома 4. Максимальное расстояние между разбиениями множества n равно ³⁾.

Имеет место следующий результат [3].

Теорема. Мера близости разбиений, удовлетворяющая аксиомам I-4 существует и определяется единственным образом.

Можно проверить, что аксиомы 1-4 выполняются для следующей меры:

(*)

55

1, если и находятся в одном классе :

где  0, если и находятся в разных классах .

Аналогично определяются величины ( для ).

Таким образом, если признать аксиомы 1-4 естественными, то следует вычислять по формуле (*); в силу теоремы никакая другая мера не удовлетворяет всем аксиомам 1-4 одновременно.

Подобно тому как в геометрическом пространстве для нескольких зафиксированных точек можно находить центр тяжести, так и в множестве всех разбиений на n , геометризованном мерой , можно для нескольких разбиений находить усредненное разбиение. Приведем точную формулировку этого понятия. Пусть заданы разбиения . Расстоянием от разбиения до множества разбиений { } называется . Усредненным разбиением по отношению к { } называется разбиение , для которого это расстояние минимально, т.е.

Рассмотрим теперь некоторые задачи обработки данных социологического обследования и методы их решения в терминах меры .

Классификация.

Под классификацией ( таксономией) обычно понимают разбиение обследованной совокупности на группы объектов, "похожих" в выбранной системе признаков. В нашей терминологии классификация — это разбиение множества и на классы "близких' по системе признаков объектов .

Если система состоит из одного признака , то классификацией является соответствующее разбиение ,если имеется да признака и , то классификация - это разбиение, среднее для и . В общем случае (для т признаков) мы предлагаем в качестве классификации брать усредненное ( в вышеопределенном смысле) разбиение по отношению к множеству разбиений

56

Заметим, что для применения данного метода классификации в отличие от известных сейчас методов [4] не нужно знание расстояний между объектами . Именно определение расстояний меду между является камней преткновения для существующих методов [4], поскольку для этого необходимо соизмерять значения различных признаков.

Аналогичным образом, если имеется насколько классификаций данного множества по разным системам признаков, то классификацию по всем признакам одновременно находим как усредненное разбиение по отношению к данным разбиениям.

Распознавание образов [4].

Пусть N объектов уже расклассифнцированы в соответствии c принимаемыми ими значениями признаков Требуется для некоторого (N+1)-го объекта с данными значениями признаков указать, в каком классе он должен находиться.

Для решения этой задачи нужно присоединить (N+1)-й объект к первоначальной совокупности, рассмотреть разбиения на полученном множестве из N+1 объекта и найти усредненное по отношению к ним разбиение , согласно которому и следует классифицировать (N+1)-й объект.

Заметим, что при малом N разбиение будет, возможно, меняться при добавлении новых объектов (что соответствует этапу самообучения), а для больших N будет относительно, стабильным, так что можно будет сразу определять класс(N+1)-го объекта, не прибегая к отысканию .

Оценка взаимосвязи признаков.

Содержательные соображения показывают, что близкие признаки характеризуются близкими разбиениями. Поэтому примем меру близости признаков пропорциональной мере близости соответствующих разбиений . Для удобства выберем коэффициент пропорциональности таким, чтобы максимальное расстояние между признаками равнялось 1.

Тогда в соответствии с формулой (*)

(**)

57

Тот факт, что , означает, что признаки P и Q дублируют друг друга; означает, что признаки P и Q независимы.

Заметим, что есть, по сути дела, статистическая оценка вероятности того, что в генеральной совокупности произвольные два объекта находятся в одном классе одного из разбиений и в разных классах другого разбиения. Легко доказать несмещенность [I] этой оценки.

Оценка значимости признаков.

Пусть на множестве n задано некоторое разбиение . Понятно, что значимость признака P для выявления разбиения тем выше, чем ближе разбиения и . Следовательно, значимость признака по отношению к разбиению можно принять обратно пропорциональной расстоянию .

Абсолютная значимость признака есть его значимость по отношению к классификации, описанной в .

Здесь, как обычно, значимость признака понижается в смысле его информативности. Однако при конкретных исследованиях такую значимость часто трактуют как "силу влияния" признака P на фактор, порождающий разбиение . То, что такая трактовка не лишена оснований, подтверждается тем, что в конкретных ситуациях она не противоречит сложившимся представлениям.

. Измерение скрытых признаков (латентный анализ [5]).

Рассмотрим задачу измерения относительно независимых факторов по данной системе зависимых признаков.

Такая задача обычно решается для количественных признаков методами факторного анализа: по данным признакам строятся их линейные комбинации (факторы), корреляция между которыми равна 0[6].

В случае классификационных признаков поступим следующим образом.

Составим матрицу расстояний между признаками и разобьем признаки на группы, внутри которых признаки максимально близки, а в разных группах — максимально далеки. Это можно сделать, например, известными методами таксономии [4] или решая соответствующую задачу оптимизации, поставленную автором в [7]. Полученные группы и являются искомыми факторами.

58

0ни, правда, лишь относительно независимы, но и в факторном анализе такая же ситуация: равенство корреляции о лишь необходимое, но не достаточное условие независимости.

Зато здесь облегчается содержательная интерпретация факторов, поскольку они являются группами признаков. Разбиения, соответствующие факторам, получаются как усредненные разбиения по отношению к множествам признаков, составляющих факторы. Зная эти разбиения, можно, например, оценивать значимость факторов методом .

Отличительной чертой приведенных методов обработки по сравнению с существующими является то ,что они дают возможность решать широкий класс задач в рамках единого подхода, основанного на четких аксиоматических построениях.

Понятно, что в данной работе лишь намечен каркас аппарата обработки данных с единой точки зрения: не приведены необходимые алгоритмы, нет статистической разработки оценки "доверия" к получаемым по выборке результатам и т.д. При этом перспективность намеченного подхода комет быть доказана лишь успешным применением его в конкретных исследованиях.

На этом пути сделаны лишь первые шаги. На материалах обследования приживаемости населения в районах, нового промышленного освоения (руководитель канд.экон.наук Е.Д. Малинин) использовался метод при оценке значимости признаков для приживаемости. Полученные результаты естественно вписываются как в другие результаты обработки, так и в интуитивные представления.

А имеющиеся отклонения позволяют сделать выводы, подтверждаемые другими данными. Например, город, для которого значимость признака "удовлетворенность общественным питанием" существенно выше, чем в других городах, и реально значительно хуке обеспечен столовыми. Не совсем тривиальным является вывод, что субъективное мнение опрошенных о том, как влияют их доходы на

их приживаемость, довольно далеко от реального влияния (оказалось, что признак "Доход на одного члена семьи" относится к наиболее значимым, тогда как признак " Удовлетворен ли материальным состоянием семьи?" относится к наименее значимым).

59

Другой эксперимент был связан с нахождением усредненной экспертной оценки. Учителя из некоторой совокупности оценивались по мастерству тремя экспертами: директором, завучем и коллегой-учителем. Таким образом, имелось три разбиения множества учителей на группы учителей с одинаковой оценкой эксперта. Описанным методом было найдено усредненное разбиение, которое должно символизировать собой некоторого объективного эксперта.

Была проделана следующая проверка объективности найденного разбиения. Каждый из трех сотрудников Института экономики и организации промышленного производства СО АН СССР нашел усредненную оценку самостоятельно, на основе интуитивных соображений, для некоторой случайной выборки из обследованной совокупности. Оказалось, что полученное разбиение лежит в центре сферы (в геометрическом пространстве разбиений), на которой находятся остальные три усредненных разбиения, выполненные на основе интуитивных соображений.

Результат эксперимента можно интерпретировать следующим образом. Наше разбиение находится в центре, так как оно в некотором смысле представляет собой объективную оценку, а остальные разбиения дают разброс по отношению к нему в результате флуктуаций, присущих субъективным оценкам.

60

Литература

1. Юл Д.Э., Кендэл М.Д. Теория статистики. М., 1960..

2. Психологические измерения. М., 1967

3. Миркин Б.Г., Черный Л.Б. Об измерении расстояния между разбиениями конечного множества. – В сб.: Математические методы моделирования и решения экономических задач. Новосибирск, «Наука», 1969.

4. Распознавание образов в социальных исследованиях. Новосибирск, «Наука», 1968.

5. Лазарсфельд П. Логические и математические основания латентно-структурного анализа. – В сб.: Математические методы в современной буржуазной социологии. М., 1966.

6. Лоули Д., Максвелл А. Факторный анализ как статистический метод. М., 1967.

7. Черный Л.Б. Обобщение метода последовательных расчетов в одной задаче классификации. – В сб.: Математические модели и методы в социально-экономических исследованиях. Новосибирск, 1968.

61

В.Л. Устюжанинов

ИНФОРМАЦИОННЫЕ МЕРЫ И ИХ ИСПОЛЬЗОВАНИЕ В СОЦИОЛОГИЧЕСКОМ АНАЛИЗЕ

В дальнейшем изложении под объектом будет пониматься заполненная анкета, состоящая из ответов на вопросы. Множество таких анкет будет именоваться множеством объектов α. Набор вопросов для всех объектов обозначается как множество признаков F. Так как на один вопрос можно дать несколько ответов, то длю каждого признака существует множество градаций , где - количество градаций признака , равное количеству логических возможностей на вопрос, соответствующий признаку . Вероятность того, что объект по признаку попадает в градацию будем обозначать как Очевидно, набор совместных вероятностей признаков будет где Информация признака о признаке дается формулой.

(1)

62

где ) и - энтропии признаков и ; - их совместная энтропия. Свойства этих величин описаны К. Шенноном [1].

Эквивалентным признаком для данного множества признаков имеющих множество градаций назовем признак, множество градаций которого равно декартовому произведению множеств градаций каждого из признаков

Множество градаций эквивалентного признака обозначим как . Очевидно, что . Условимся, что разбиение множества объектов на подмножества по признаку порождает множество подмножеств объектов

Процедура образования эквивалентного признака соответствует замене комплекса вопросов в анкете на один сложный вопрос.

Введение эквивалентного признака удобно в тех случаях, когда, например, изучается связь между комплексами признаков. Тогда можно заменить рассмотрение связи между комплексами признаков на рассмотрение связи между эквивалентными признаками, представляющими эти комплексы признаков.

За меру различия между подмножествами объектов и по признаку принимается «разностное информационное отношение»

(2)

Здесь - потеря информации признака о признаке при объединении градаций и в признаке .

(3)

63

где штрихованные величины вычисляются после объединения градаций, а не штрихованные – до объединения.

Докажем несколько свойств:

1.

Правая часть этого неравенства следует из (3). Докажем левую часть неравенства. Для этого достаточно показать, что

(4)

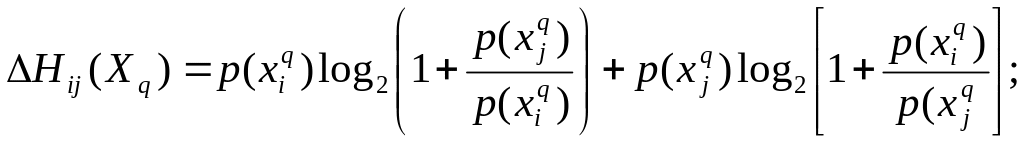
(5)

Покажем, что

К последнему выражению применимо неравенство Иенсена из теории выпуклых функций [2], так как и функция выпукла вверх.

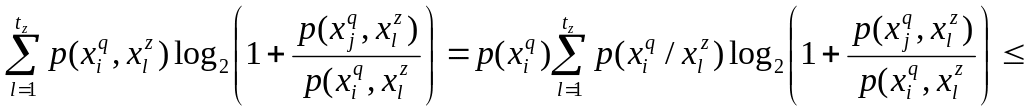
64

2. Если множества объектов и максимально различны по признаку , то и .

Определение 1. Множества объектов и называются максимально различными по признаку , если – пустое множество.

Очевидно, что в этом случае в не будет ни одного объекта одинакового по с каким-либо другим объектом из

Определение 2. Множества и называются одинаковыми по признаку , если

Учитывая сказанное, нетрудно получить, что

Пусть и Введем Тогда будет иметь вид

График функции дан на рис. 1.

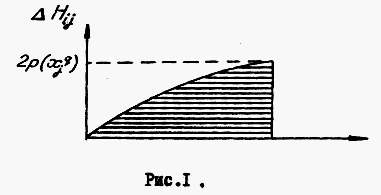
Если множества и максимально различны по признаку , то потеря информации о признаке при объединении и будет тем меньше, чем больше отношение количества объектов в и .

Из свойства 1 следует, что в общем случае значения лежат в заштрихованной области (см. рис. 1).

65

3. Если и одинаковы по признаку , то . Это легко доказывается, если использовать определение (2). Очевидно также, что в этом случае .

4. Если , то и одинаковы по признаку . Введем обозначения 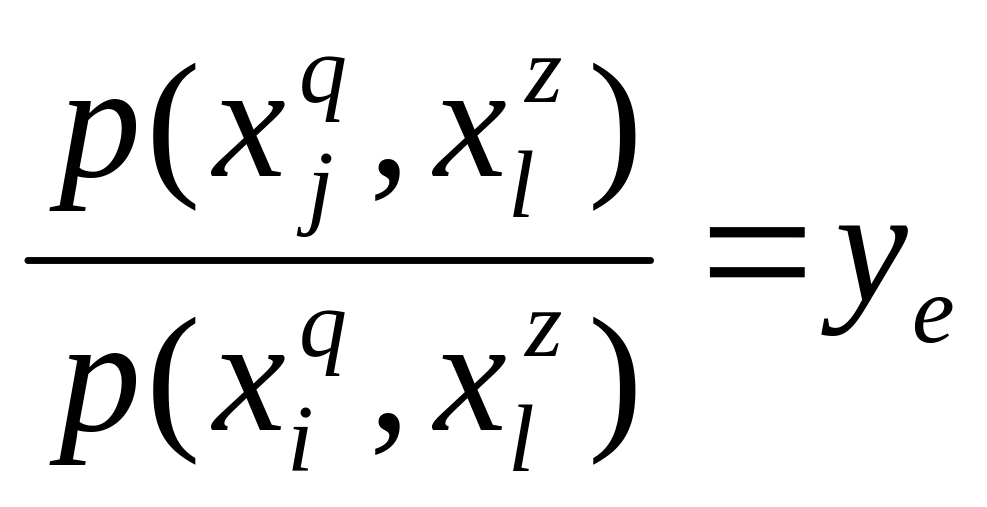и . В них запишется в виде

(5а)

Докажем, что

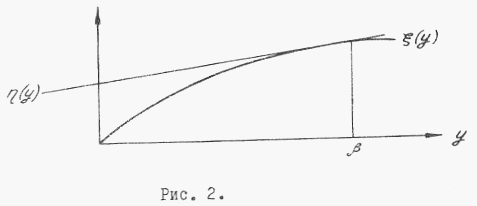
На рис. 2. даны графики и

Очевидно, что и т.е. в точке кривые и касаются. Покажем, что левее и правее точки разница и положительна. Для этого разложим функцию в ряд Тейлора . Получим Единственность точки касания следует из графиков и .

66

Если , то , т.е. для или 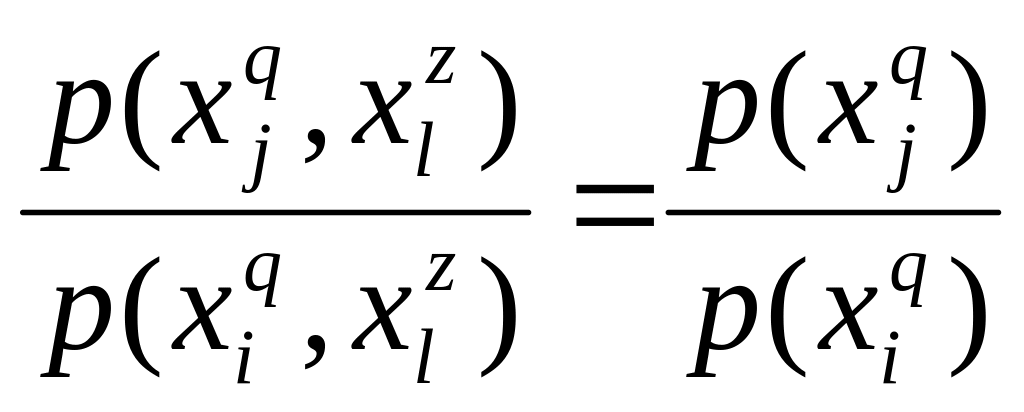. Отсюда следует, что и это доказывает свойство.

5. Если , то множества объектов и максимально различны по признаку .

Используя обозначения, принятые при доказательстве свойства 4, нетрудно показать, что

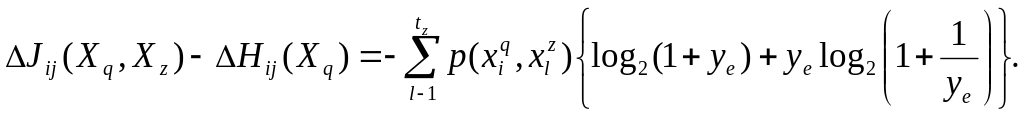
Из равенства следует, что

Это равенство выполняется только тогда, когда или т.е. при условии, если то и наоборот. Отсюда следует, что – пустое множество, т.е. и максимально различны по признаку .

Пример 1. Группе опрошенных задавали два вопроса: «Ваш возраст?» и «Чем Вы занимаетесь в свободное время?». Было введено несколько возрастных групп и две группы по видам занятий в свободное время.

К первой группе по признаку , относились те, кто предпочитал в свободное время заниматься спортом, совершать прогулки, любил бывать на улице. Ко второй группе относились домоседы, предпочитавшие быть в кругу семьи. К первой возрастной группе относились самые молодые из опрошенных, к последней - самые старшие.

Замерим разницу между различными возрастными группами опрошенных по признаку , если известно, что распределение условных вероятностей имеет следующий вид:

67

Здесь - вероятность того, что член возрастной группы предпочитает занятие в свободное от работы время.

Разница между различными возрастными группами измеряется с помощью меры различия Результаты удобно представить в виде следующей таблицы.

Таблица 1.

№ группы
	0	0,0551	0,4058	0,4556
	0,0551	0	0,2740	0,4058
	0,4058	0,2740	0	0,0559
	0,4556	0,4058	0,0551	0

Здесь стоит на пересечении строки i со столбцом j. Видим, что наиболее далекими по признаку оказались группы и , т.е. самые молодые из опрошенных и самые старшие. Это же было видно и из распределений условных вероятностей, помещенных выше. Наиболее похожи друг на друга группы и , что объясняется их близостью друг к другу по возрасту, а также группы и .

Может возникнуть вопрос об области применения, продемонстрированной на данном примере методики.

По-видимому, настоящий аппарат может быть применен в тех случаях, когда различия между группами объектов по некоторому

68

признаку (или комплексу признаков) заранее не очевидны и мера различия может быть замерена экспериментально, кроме того, в поиске полярных, т.е. наиболее удаленных или наиболее близких по некоторому признаку групп объектов, а также в поиске таких признаков, по которым данные пары объектов наиболее различались бы, и т.д.

Разностное информационное отношение обладает тем свойством, что с его помощью можно сравнивать отдельные объекты на схожесть друг с другом по некоторому признаку .

Покажем это. Пусть имеются объекты и . Признак принимает на объекте множество значений а на объекте множество значений Иными словами на вопрос опрашиваемый дает ответов, а опрашиваемый дает ответов. Допустим, что опрашиваемые и дают m одинаковых ответов на вопрос . Тогда множество будет иметь m элементов.

Введем - вероятность того, что на объекте примет значение , и , которая понимается аналогично. Определим также

Очевидно, что

если , то

если , то

если , то

если , то

Формула (7) для данного случая имеет вид

69

где

Используя значения вероятностей, можно показать, что два первых члена в (9) равны нулю, а третий равен Итак,

Очевидно, что и . Подставляя в (6) и вместо и соответственно и используя (4, 5), получим

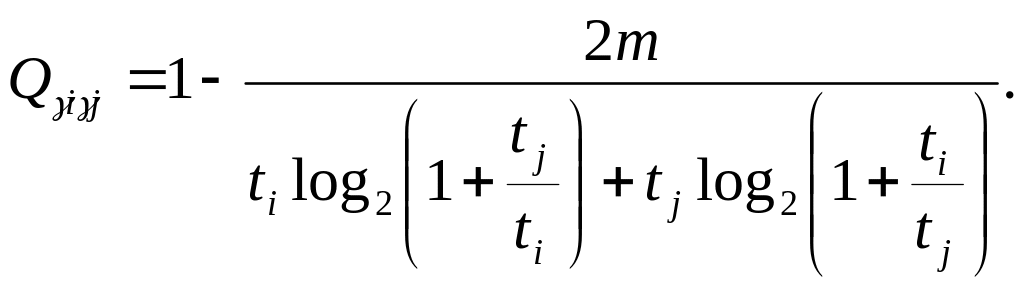(7)

Это и есть мера различия между двумя объектами.

Пример.

Допустим, что . Отсюда следует, что Если и , то . Если же Если и , то .

В первом случае объекты совпадают по , а во втором случае они различны, т.е. если признак может принимать на объекте не более одного значения, то объекты по такому признаку могут быть либо одинаковыми, либо максимально различными.

Пример 2. Петру и Юрию задали вопрос: «На какие издания Вы подписались в этом году?» Петр сказал, что он выписал «Известия», «Комсомольскую правду», «Техника-молодежи», «Новый мир», и «Советский спорт». Юрий ответил что он будет получать «Правду», «Новый мир», «Советский спорт», «Советский экран» и «Новое время».

Замерим различие между Юрием и Петром. Количество ответов, данное Петром на поставленный вопрос, будет Количество ответов, данное Юрием на поставленный вопрос, будет Количество совпадающих ответов, данных Юрием и Петром, будет Теперь по формуле (7) вычислим значение различия между ответами Юрия и Петра - Q_ЮП=0,6. Если бы Юрий и Петр подписались на одни и те же газеты и журналы, то Q_ЮП=0. Если же Юрий подписался не на те газеты и журналы, на которые подписался Петр, то Q_ЮП=1.

70

Естественным обобщением парной меры близости множеств объектов является мера близости для множеств объектов, количество которых больше двух.

Пусть имеется множество множеств объектов , различающихся по эквивалентному признаку . Из выберем произвольные множества объектов ; . Введем и изучим меру различия между этими множествами по признаку .

Вероятность принадлежности объекта к множеству обозначим Если объект, принадлежащий к по признаку попадает в градацию , то вероятность этого события обозначается Введем также совместную вероятность

За меру различия множеств по признаку принимается величина

(8)

где

Докажем основные свойства этой меры.

1. и

2. Если множества объектов одинаковы по , то и Q=1. Доказательства аналогичны тем, которые даны для парной меры.

3. Если множества объектов максимально различны по , то Введем множества градаций по признаку , в которые попадают объекты из Из смысла максимального различия множеств следует, что - пустое множество. Поэтому произвольная градация может либо принадлежать одному из множеств , либо не принадлежать ни одному из этих множеств.

Если то и величина

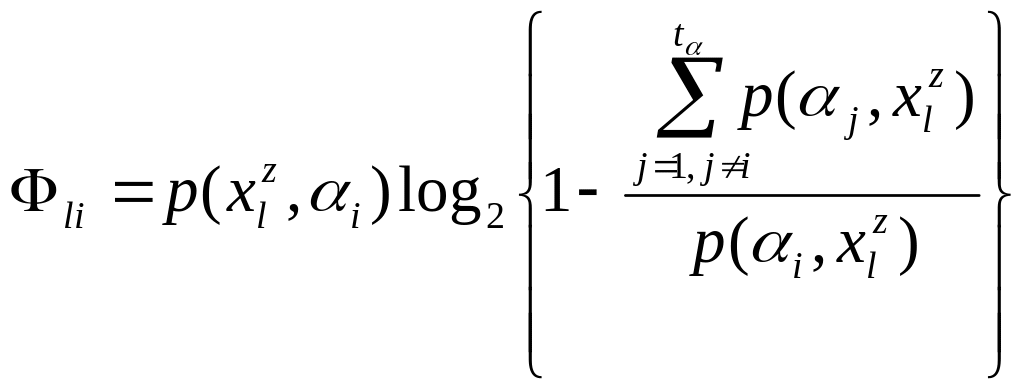
72

равна нулю.

Если то и .

Если же , то и , т.е. , т.к. , что доказывает это свойство.

4. Если Q=0, т.е. если , то множества объектов максимально одинаковы по признаку ^*).

5. Если Q=1, т.е. если , то множества объектов максимально различны по . Из равенства и выражения (8)

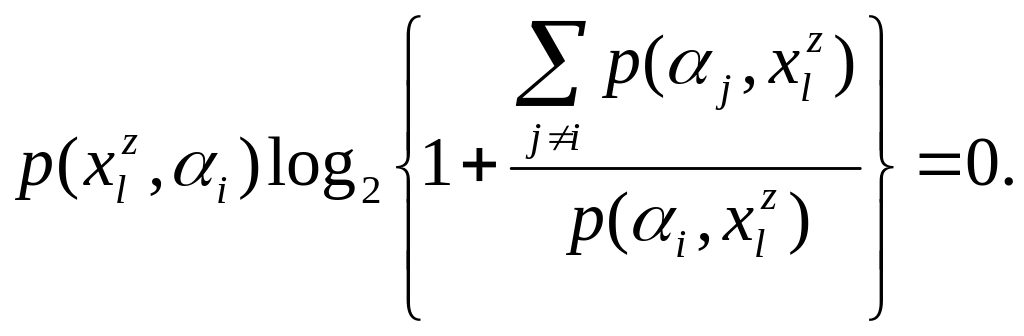
Если , то необходимо, чтобы и только .

Если же , то

Допустим строгое неравенство. Докажем, что в этом случае принадлежит только одному множеству из

В самом деле, если допустить, что принадлежит r, то из равенства

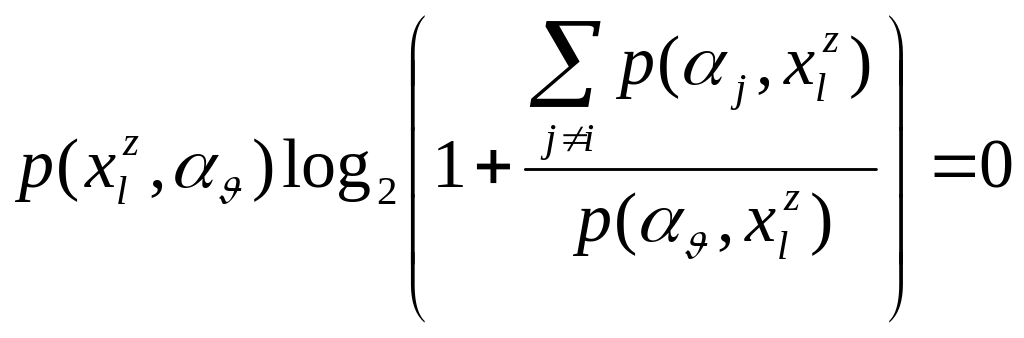
следует, что т.е. и только , что и требовалось доказать.

В частном случае меры близости для всех множеств , образованных с использованием признака , нетрудно показать, что будет выражаться формулой

(9)

72

Здесь - потеря информации при объединении всех множеств объектов в одно, равная информации ; - потеря энтропии признака , равная .

Пример 3. В анкете выпускника содержится вопрос: «Где Вы думаете учиться? (Укажите название учебного заведения)». Исходя из названия учебного заведения, указанного при ответе, школьников можно было разбить на группы по отраслям народного хозяйства и культуры, в которых они, вероятнее всего, должны будут работать по окончании выбранного учебного заведения. Подобное разбиение на группы будем называть разбиением на группы по признаку , где - символ, присвоенный нами ответу на вышеуказанный вопрос: «Где Вы думаете учиться?»

Символом обозначим признак, обозначающий информацию о том, к какой отрасли относятся учебные заведения, в которые реально попали выпускники после окончания школы. Каждую группу выпускников, полученную в результате разбиения по признаку , разбивали на подгруппу по признаку , т.е. производили двухпризнаковую группировку выпускников. Ниже приведены возможные ответы по признакам и , принятые авторами анкеты.

‑ нет ответа;

- промышленность тяжелая;

- промышленность легкая;

- строительство;

- сельское хозяйство

- лесное –“-

- транспорт;

- связь;

- торговля;

- общественное питание;

- жилищно-коммунальное хозяйство;

- здравоохранение;

- просвещение;

73

- наука;

- искусство;

- кредитные учреждения;

- аппарат государственного и хозяйственного управления;

- прочие.

Через обозначим группу выпускников, давших ответ l по признаку (т.е. выбравших отрасль l, одну из вышеуказанных отраслей), а через группу выпускников, попавших в отрасль j по признаку . Количество выпускников, давших ответ на вопрос , обозначим . Аналогично введем . Количество выпускников, планировавших свое будущее в соответствии с ответом на вопрос и реально попавших в такие учебные заведения, что их ответы по признаку оказались обозначим . Например, - количество выпускников, планировавших по окончании школы поступить в учебные заведения, готовящие специалистов для тяжелой промышленности, а реально поступивших в учебные заведения связи.

Введем условную вероятность того, что опрошенный, давший ответ на вопрос , дает ответ на вопрос . Она равна доле опрошенных, давших ответ на вопрос и ответ на вопрос , из общего количества людей, давших ответ на вопрос , т.е.

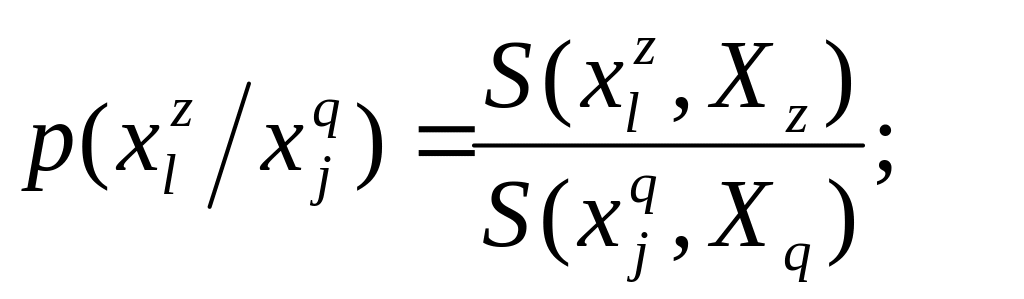
Таблица условных вероятностей для конкретного случая приведена ниже.

74

Таблица 2.

q\z
	0,006	0,39						0,06				0,06	0,06	0,37
				0,05										0,85		0,05		0,05
	0,18			0,09										0,18	0,09			0,27

В пустых клетках подразумеваются нули; строки и столбцы, состоящие из одних нулей вычеркнуты. Из 18 групп выпускников, полученных при разбиении их на группы по признаку , рассмотрены лишь 3, так как все остальные группы либо пусты, либо содержат по 3-4 человека.

Вычислим общую меру близости по признаку между группами выпускников, образованными при делении всей совокупности выпускников по признаку . Иными словами, определим, насколько близки по своим ответам выпускники, относящиеся к группам , , . Вспомним, что эти выпускники, поступившие после окончания школы в учебные заведения, готовящие специалистов для тяжелой промышленности ( ), для науки ( ) и для прочих отраслей ( ). Вычислим эту меру близости по формуле (9), используя (1) и (3). В нашем слу-

75

чае Выше показано, что если , т.е. , то выпускники из групп , , максимально различны по своим ответам на вопрос . Т.е. если выпускники из группы дают ответы ответам на вопрос , то ни один человек из группы не дает подобных ответов. Например, выпускники из могут давать в этом случае ответы а - ответы В этом и только случае , т.е. группы , , максимально различны. Реальная ситуация, как это видно из табл. 1, совершенно иная. Так некоторые члены группы дают тот же ответ , что и большинство выпускников из . Некоторые члены группы дают общие ответы с (это , , ) и с (это , , ). Т.е., между группами , и есть некоторое сходство и это сходство можно заметить с помощью общей меры близости .

Заметим, что группы (пусть это будут и ) одинаковы по признаку , если процент людей в группе , давших ответ , равен проценту людей в группе , давших тот же ответ из всех возможных ответов на вопрос . Иными словами, В этом и только в этом случае .

Приведем пример групп, весьма похожих друг на друга. Среди других вопросов «Анкеты выпускника» были такие вопросы:

- «Каков средний месячный доход одного члена семьи?»^*)

- «Что Вы думаете делать после окончания школы?»

Возможные ответы на 1-й вопрос:

- нет ответа;

- до 10 руб.;

- 10, 1 – 20 руб.;

- 20,1 – 30 руб.;

76

- 30,1-40 руб.;

- 40,1-50 руб.;

- 50,1-60 руб.;

- 60,1-70 руб.;

- 70,1-80 руб.;

- 80,1 руб. и выше.

Возможные ответы на 2-й вопрос:

- работать;

- совмещать работу и учебу;

- учиться.

Распределение условных вероятностей представлено в табл. 3.

q\z
	0,14			0,14	0,21	0,21			0,14	0,08
	0,12	0,02		0,06	0,15	0,20	0,10	0,10	0,08	0,17
	0,06		0,08	0,13	0,17	0,19	0,11	0,17	0,03	0,06

Мера различия между группами , , равна , т.е. мала, и названные группы в общем сходны.

Из приведенного примера следует такой вывод: исследование по признаку групп людей, образованных по признаку , тем «выгоднее» для исследователя, чем больше мера , т.е. тем более отличаются друг от друга по группы, образованные при делении всей совокупности людей по признаку .

Допустим, что методическая цель исследования – выявить комплекс таких вопросов в анкете (или хотя бы один вопрос), что-

77

бы, зная ответы опрошенного на эти вопросы, можно было бы предсказать его ответы на другой, интересующий исследователя вопрос. Так как комплекс вопросов всегда можно свести к одному сложному вопросу, то достаточно рассмотреть эту задачу для случая одного вопроса, с помощью которого удобнее всего угадывать ответы на другой. Переведем задачу на формальный язык. Идеальным предсказанием было бы предсказание, которое позволило, не зная, в какую группу попал объект по признаку , однозначно указать группу, в которую попадает объект по признаку .

у нас 6 групп: , , , , , , , , , , а по признаку - 3 группы: , , .

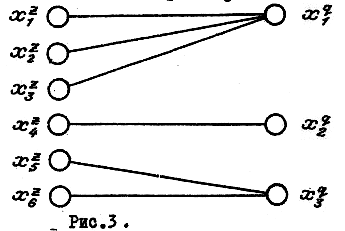
На рис. 3 стрелками показано, в какие группы по признаку попадают объекты,

оказавшиеся в группах по признаку . Видим, что объекты из группы , , попадают в группу , а объекты из - в .

В этом случае, зная ответ на вопрос , можно однозначно указать ответ на вопрос . Вспомним, что именно в ситуации, изображенной на рис. 3, группы объектов , , максимально различны по признаку , т.е. . Следовательно, можно утверждать, что наиболее выгоден для предсказания ответов по , случай, когда .

Если , то это означает, что есть группы, по признаку , которые не являются максимально различными по признаку . Если это и , то обязательно в обеих группах найдутся объекты, попавшие в одну и ту же группу, по признаку . Сказанное поясняется рис.4.

78

В этом случае, зная группу объектов, в которую попал объект по , невозможно однозначно указать группу объектов, в которую он попал по . Итак, чем больше , чем ближе оно по своему значению к 1, тем точнее можно предсказывать (для точного предсказания необходимо, чтобы было как можно ближе к ).

Если нужно среди признаков выбрать такой, используя который можно предсказать ответы по вопросу q наиболее точно, то следует брать тот , у которого мера максимальна.

Допустим, что для предсказания ответов по вопросу q используется комплекс вопросов, т.е. комплекс признаков, тогда

Из теории информации известно, что если из комплекса признаков X удалить хотя бы один признак, то , где через обозначен комплекс признаков X без удаленного признака. Отсюда Последнее неравенство означает, что предсказание ответов по вопросу не может быть лучше предсказания с использованием . Говоря «социологическим» языком, если предсказание ответов по какому-нибудь вопросу в анкете с использованием всех вопросов анкеты дает плохие результаты, то

79

любая комбинация вопросов, используемая для предсказания, не даст лучшего результата, т.е. анкета не отвечает цели исследования.

Пусть имеется множество объектов , исследуемых по признаку , что подразумевает разбиения на подмножества по признаку и вычисление распределений вероятностей в момент времени .

Здесь , как и прежде, есть количество градаций (в общем случае) эквивалентного признака . Для простоты допустим, что во время всего исследования, от момента времени до , множество объектов содержит одни и те же элементы.

Если хотя бы для одного выполняется равенство , то будем говорить о наличии измерения по признаку , происшедшего с множеством объектов за период от до и рассматриваемого как целое.

Запишем множество градаций по признаку , в которые попали объекты в момент . Получим.

Определение 3. Изменение, происшедшее с с момента времени до момента времени назовем максимальным, если - пустое множество.

Определение 4. Изменение, происшедшее с с момента времени до момента времени назовем минимальным, если для всех .

Для измерения, происшедшее за период до можно использовать парную меру различия для групп объектов . , поскольку одно и то же множество, изучаемое в два разных момента времени, можно представить как два различных множества, сравниваемых друг с другом по одному и тому же признаку .

Если распределение вероятностей совпали, то . И наоборот, из следует, что за время от до

80

изменения не произошло.

Если измерение максимально, то . И наоборот, если , то за время от до с множеством произошло максимальное изменение по признаку . Изменения, заключенные между этими крайними случаями, естественно приведут к .

За скорость изменения в момент примем отношение

И (10)

Очевидно, что, чем меньше срок, за который произошло изменение, тем выше его скорость. Так как , то И .

В заключение приведем вывод формулы , где - произвольные моменты времени. Выпишем пригодную в данном случае формулу для парной меры близости между множествами объектов и затем преобразуем ее:

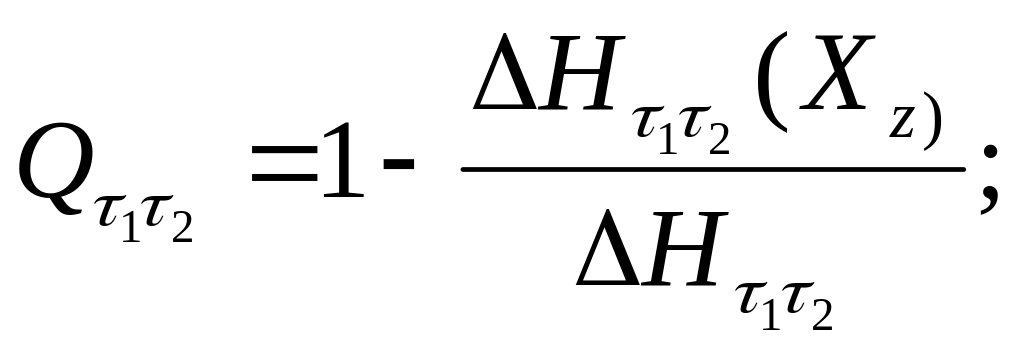
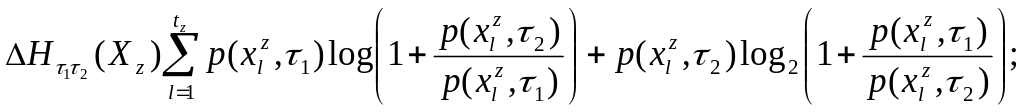(11)

Здесь - то же, в момент времени .

Упростим учитывая, что по допущению в начале параграфа. Тогда

81

=1 или = 1 ( X ). Вероятность p(x ,  ) равна p(x ,  ) = S(x ,  )  S k = 1, 2; l = 1, t ,

где S(x , t ) – количество объектов, попавших в градацию по признаку X в момент  . Так как

S( ) = S( ), то p(x ,  ) = p( )p(x   ) = p(x   ).

Учтя это, получим

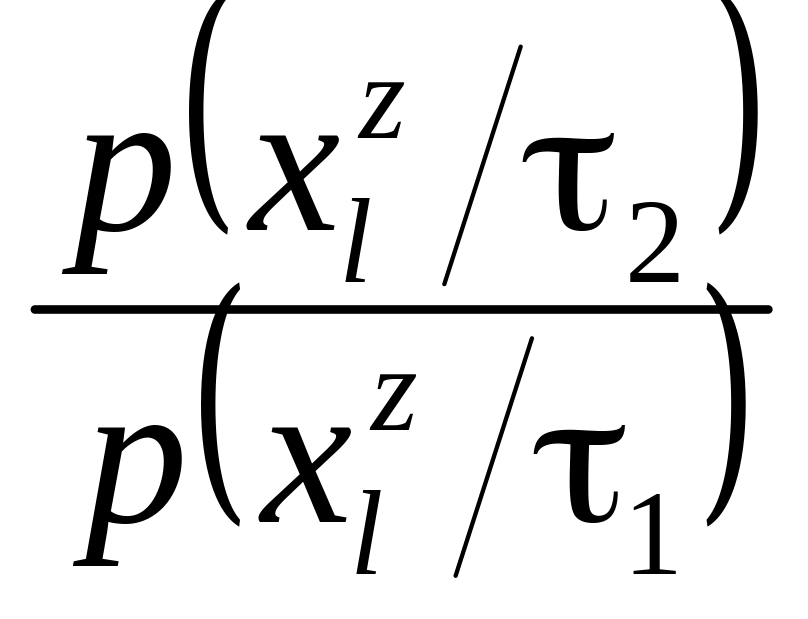
(X ) = p(x   ) log 1 + + p(x   ) log 1 + ;

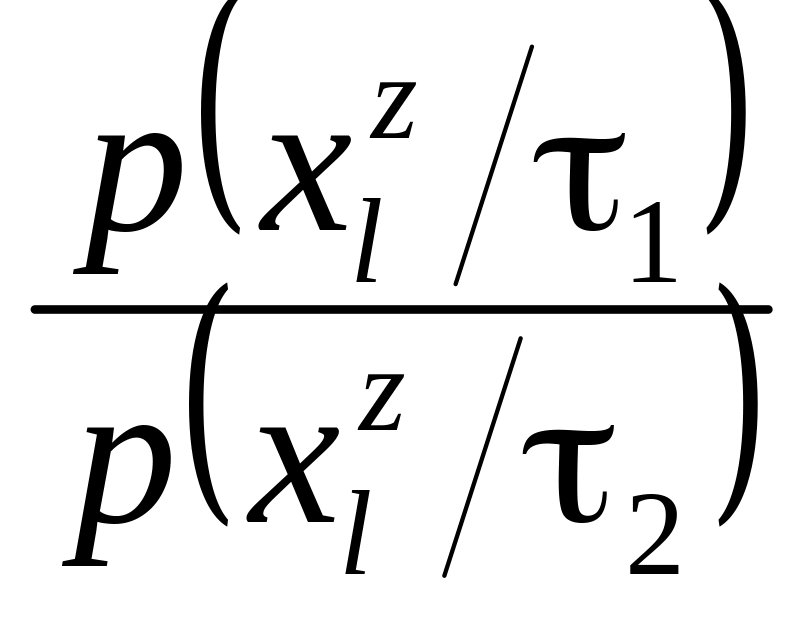= 1 ( X ).