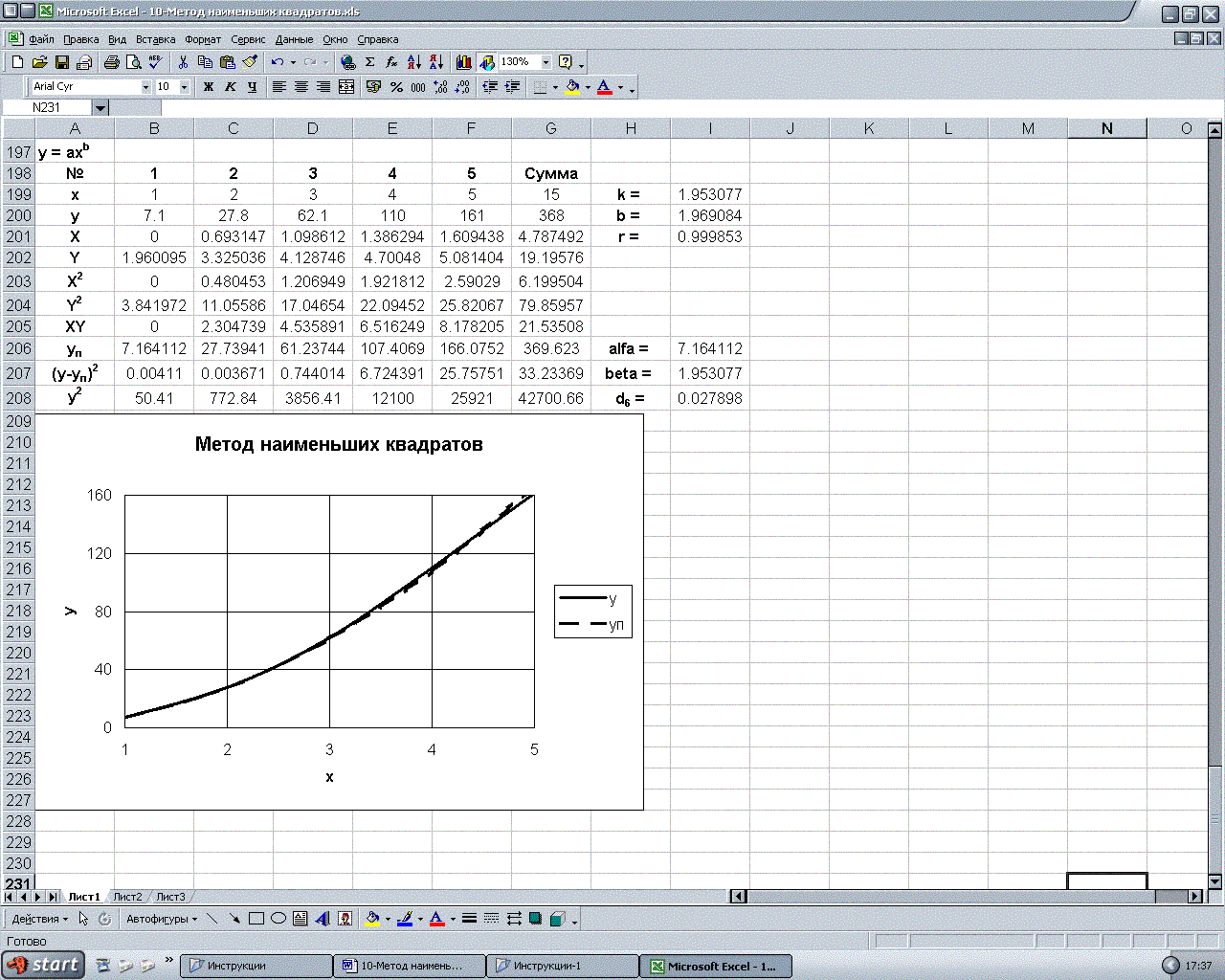
Типовой отчет.
Результаты эксперимента представлены в виде таблицы значений переменных x и y :
-
xi
1
2
3
4
5
yi
7,1
27,8
62,1
110
161
Для семи вариантов аппроксимирующих зависимостей с двумя параметрами и методом наименьших квадратов определить их оптимальные значения, вычислить коэффициенты регрессии и оценки уклонения аппроксимирующих зависимостей от экспериментальных точек, на основе чего выбрать лучший вариант эмпирической формулы.
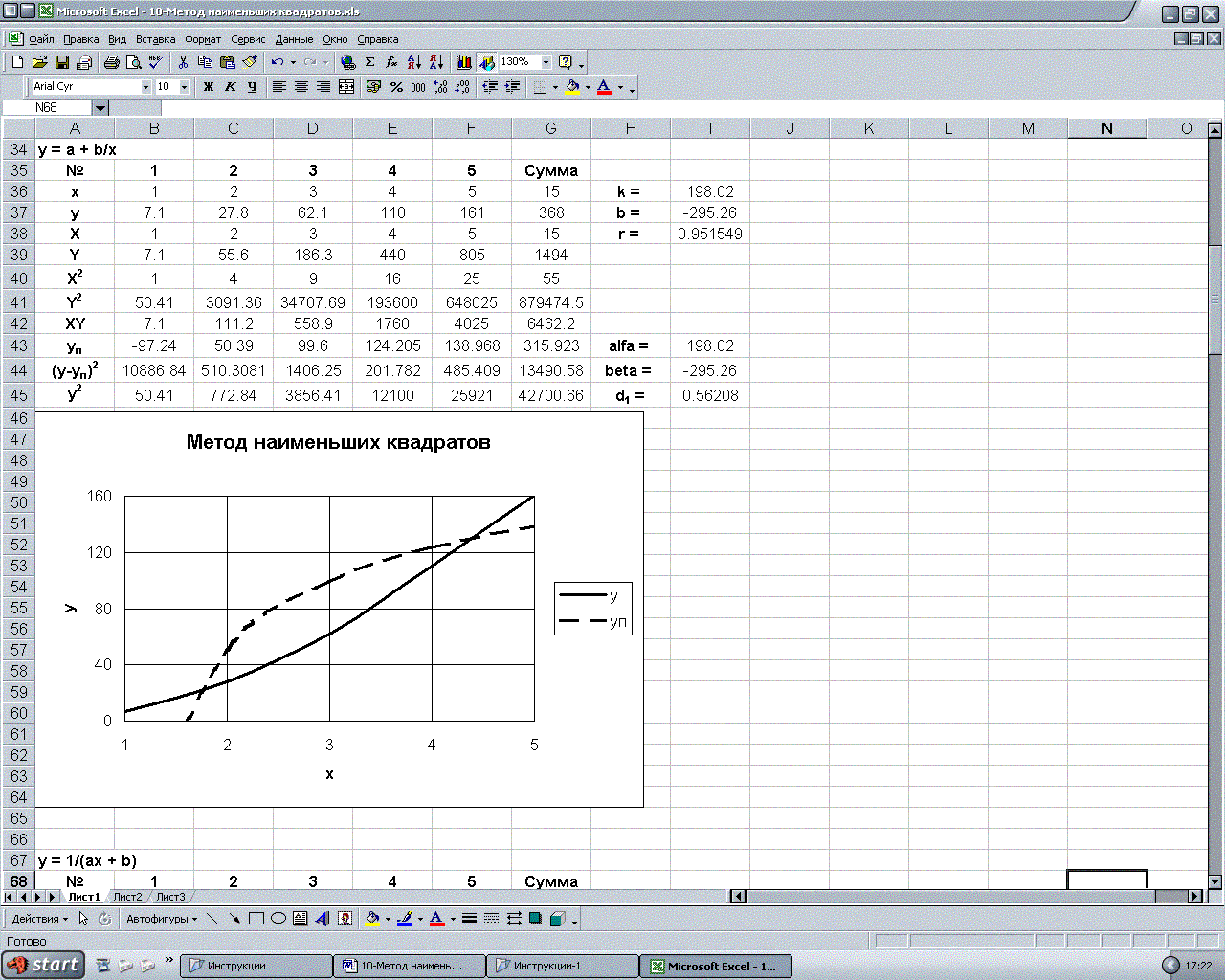
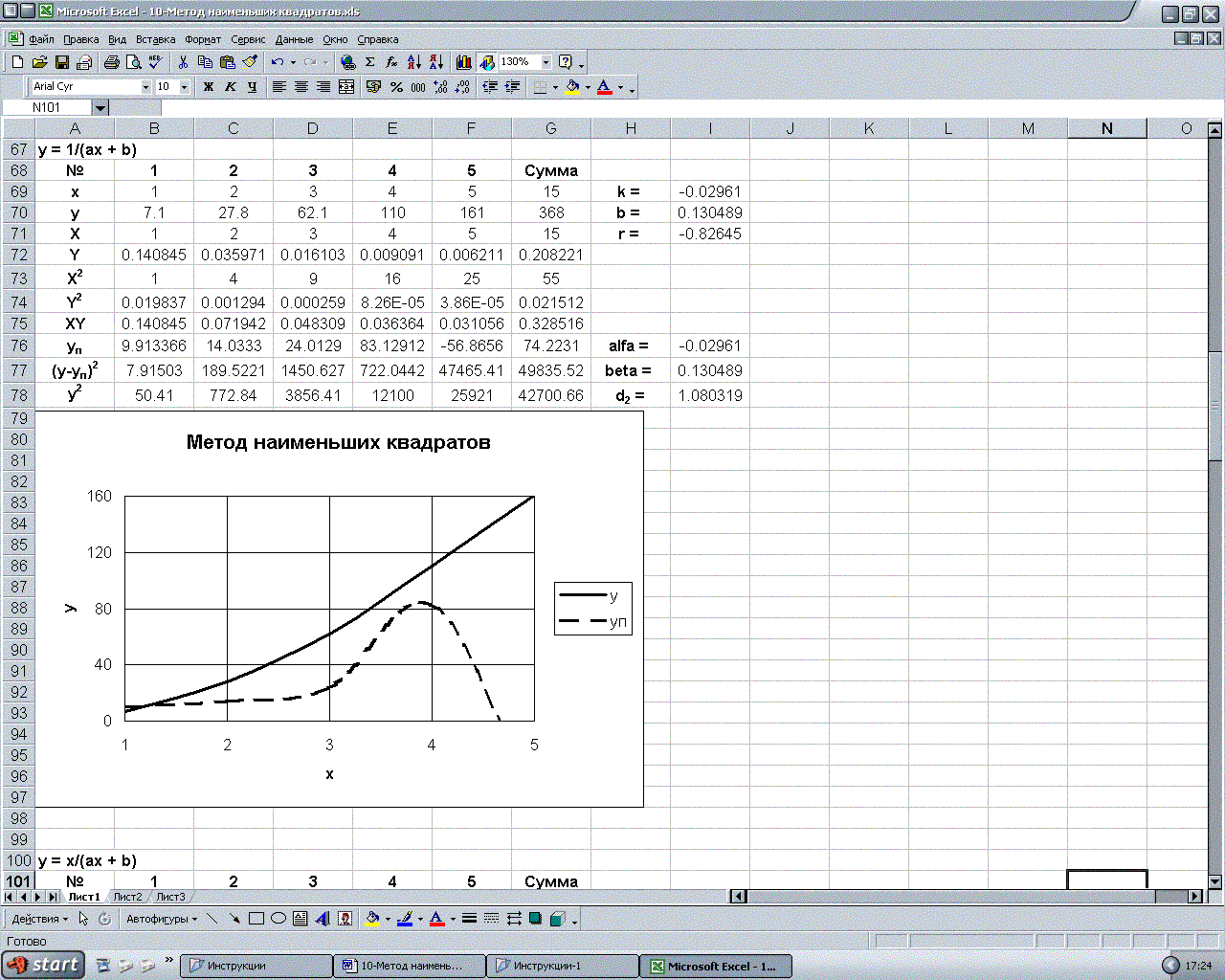
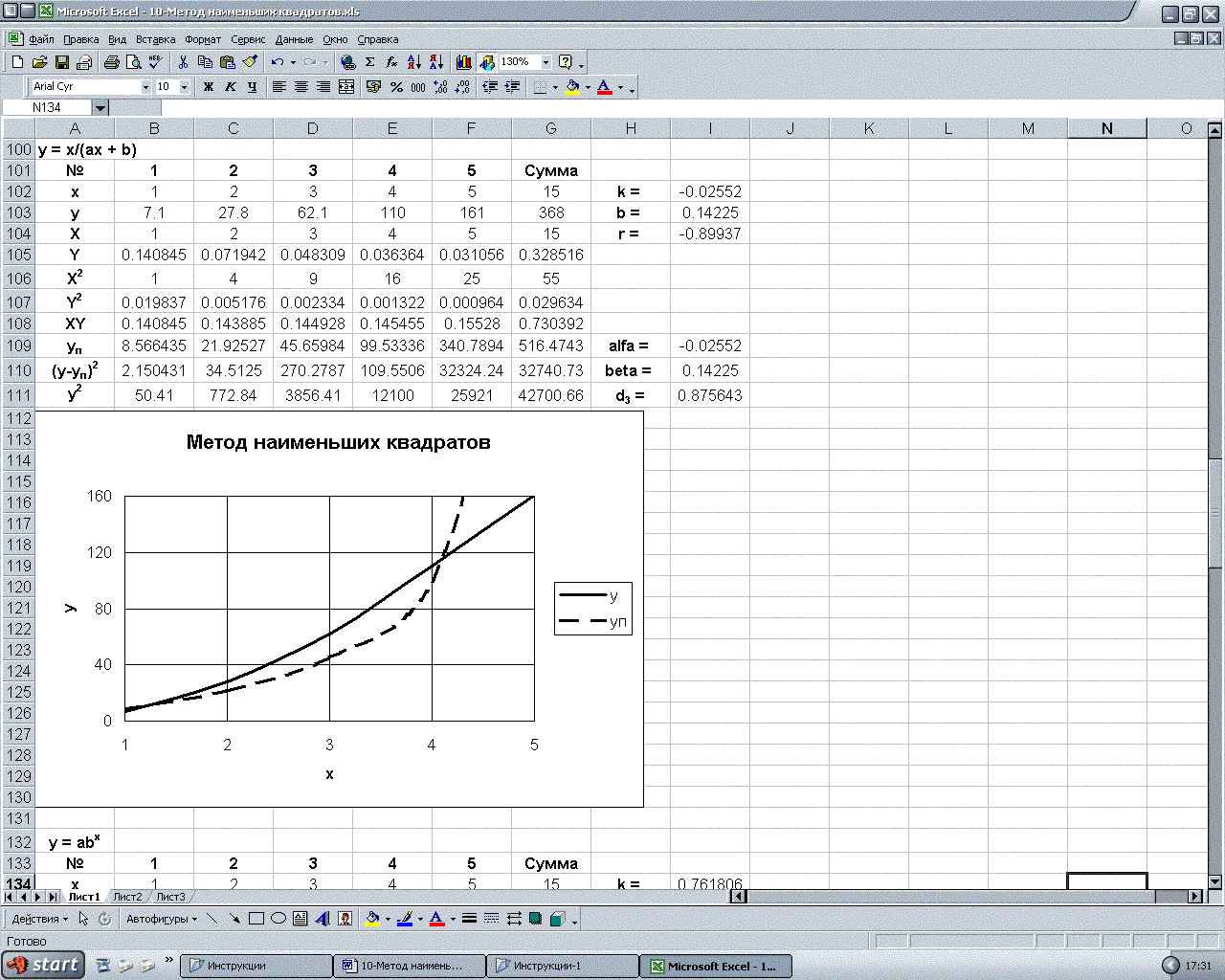
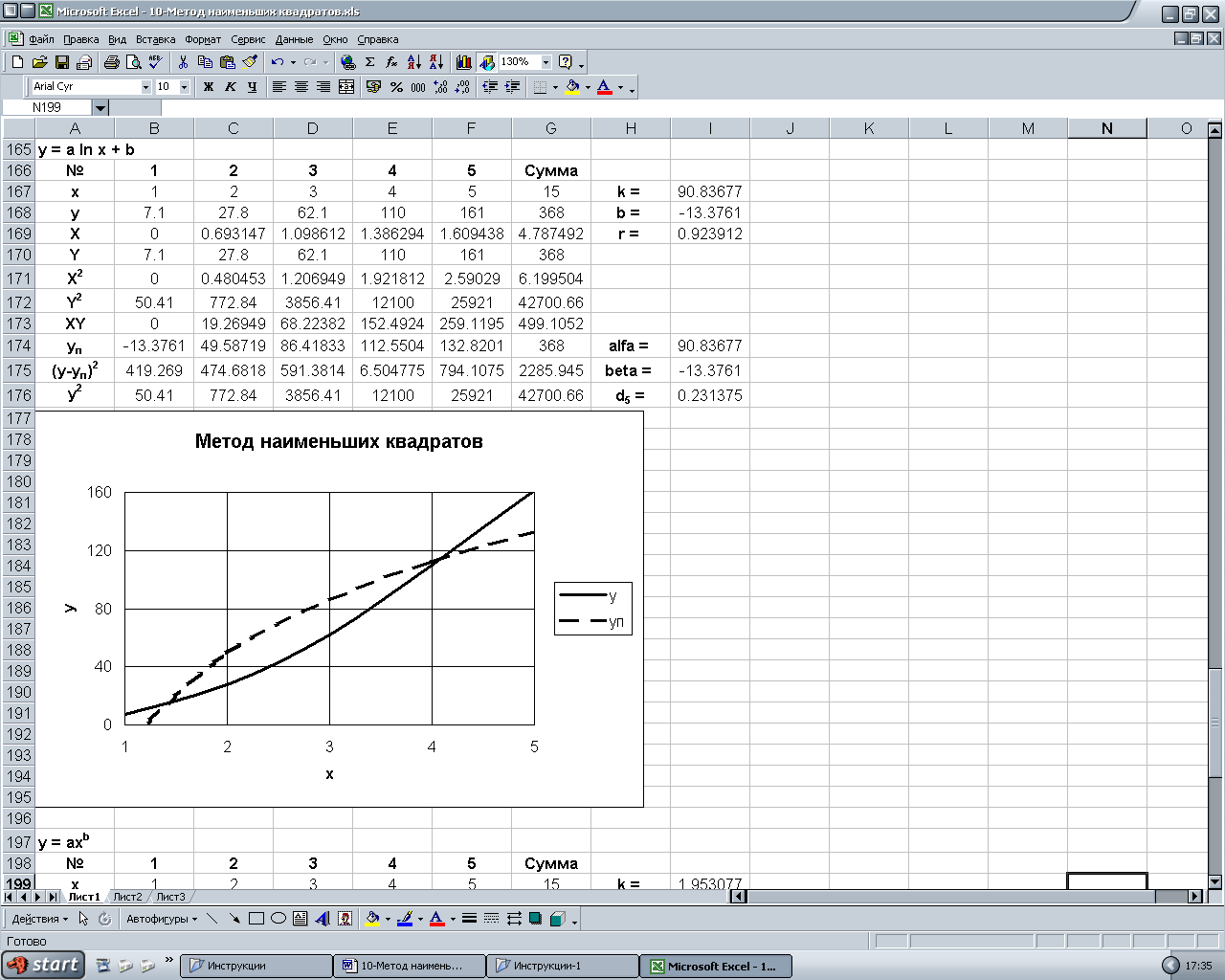
Результаты применения метода наименьших квадратов к эмпирическим формулам представлены в таблице.
Функция |
k |
b |
r |
|
|
d |
y = x + |
39 |
-43,4 |
0,987 |
39 |
-43,4 |
0,097 |
|
198,02 |
-295,26 |
0,915 |
198,02 |
-295,26 |
0,562 |
|
-0,0296 |
0,130 |
-0,826 |
-0,0296 |
0,130 |
1,080 |
|
-0,0255 |
0,142 |
-0,899 |
-0,0255 |
0,142 |
0,876 |
y = x |
0,762 |
1,554 |
0,970 |
4,729 |
2,142 |
0,271 |
y = ln x + |
90,837 |
-13,376 |
0,924 |
90,837 |
-13,376 |
0,231 |
y = x |
1,953 |
1,969 |
0,9999 |
7,164 |
1,953 |
0,0279 |
Наименьшей оценкой уклонения аппроксимирующей зависимости от экспериментальных точек, равной d6 = 0,0279 , обладает функция .
Варианты.
Результаты эксперимента представлены в виде таблицы значений переменных x и y . Для семи вариантов аппроксимирующих зависимостей с двумя параметрами и методом наименьших квадратов определить их оптимальные значения, вычислить коэффициенты регрессии и оценки уклонения аппроксимирующих зависимостей от экспериментальных точек, на основе чего выбрать лучший вариант эмпирической формулы.
1. |
xi |
1 |
2 |
3 |
4 |
5 |
2. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
1,1 |
1,4 |
1,6 |
1,7 |
1,9 |
|
yi |
1,06 |
1,55 |
1,7 |
1,75 |
1,8 |
3. |
xi |
1 |
2 |
3 |
4 |
5 |
4. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
0,4 |
0,55 |
0,13 |
0,09 |
0,07 |
|
yi |
7,5 |
6,2 |
5,5 |
3,5 |
3 |
5. |
xi |
1 |
2 |
3 |
4 |
5 |
6. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
8,2 |
5,9 |
4,9 |
4 |
3,2 |
|
yi |
7,2 |
5,9 |
4,9 |
4 |
3,2 |
7. |
xi |
1 |
2 |
3 |
4 |
5 |
8. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
7,1 |
6,1 |
4,9 |
4, |
3,1 |
|
yi |
0,55 |
0,7 |
0,77 |
0,82 |
0,85 |
9. |
xi |
1 |
2 |
3 |
4 |
5 |
10. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
1,1 |
1,55 |
1,9 |
2,3 |
2,6 |
|
yi |
1,1 |
1,55 |
1,9 |
2,25 |
2,5 |
11. |
xi |
1 |
2 |
3 |
4 |
5 |
12. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
5,1 |
4,4 |
3,2 |
2,7 |
2,55 |
|
yi |
5,1 |
3,4 |
3,2 |
2,7 |
2,55 |
13. |
xi |
1 |
2 |
3 |
4 |
5 |
14. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
1,9 |
5,5 |
10 |
15 |
21 |
|
yi |
3 |
3,5 |
3,67 |
3,75 |
3,8 |
15. |
xi |
1 |
2 |
3 |
4 |
5 |
16. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
0,25 |
0,09 |
0,07 |
0,05 |
0,04 |
|
yi |
0,25 |
0,111 |
0,071 |
0,053 |
0,042 |
17. |
xi |
1 |
2 |
3 |
4 |
5 |
18. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
0,20 |
0,28 |
0,33 |
0,36 |
0,38 |
|
yi |
4,8 |
5,76 |
6,912 |
8,294 |
9,95 |
19. |
xi |
1 |
2 |
3 |
4 |
5 |
20. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
1 |
3,08 |
4,3 |
5,16 |
5,83 |
|
yi |
0,33 |
0,5 |
0,6 |
0,67 |
0,71 |
21. |
xi |
1 |
2 |
3 |
4 |
5 |
22. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
1,5 |
1,75 |
1,83 |
1,87 |
1,9 |
|
yi |
1 |
0,2 |
0,11 |
0,077 |
0,059 |
23. |
xi |
1 |
2 |
3 |
4 |
5 |
24. |
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
1 |
0,4 |
0,33 |
0,31 |
0,29 |
|
yi |
2,25 |
3,37 |
5,06 |
7,59 |
11,4 |
Вид рабочего листа MS Excel.
Лабораторная работа № 11
"Интерполяционная формула Лагранжа"
Элементы теории.
Пусть функция y = f(x) определена таблицей:
-
xi
x0
x1
…
xn
yi
y0
y1
…
yn
Значения аргументов xi , i = 0, 1, … , n называются узлами интерполяции. Задачей интерполяции является построение многочлена L(x), значения которого в узлах интерполяции xi равны соответствующим значениям заданной функции, то есть L(xi ) = yi , i = 0, 1, … , n. Интерполяционной формулой Лагранжа называется формула, представляющая многочлен L(x) в виде:
,
где pi (x) – многочлен степени n, принимающий значение равное единице в узле xi и нулю в остальных узлах xk , k i и имеющий вид:
.
Многочлен L(x) называют интерполяционным многочленом Лагранжа и его степень не превышает числа n.
Если функция f(x) на отрезке [ x0 , xn ] имеет непрерывные производные до (n + 1)-го порядка включительно, то погрешность интерполяционной формулы в каждой точке этого отрезка оценивается неравенством:
,
где
,
.