Варианты.

Построить кубический сплайн, интерполирующий заданную функцию на отрезке [1,00; 1,20] для равномерного разбиения с шагом h = 0,04 при краевых условиях I и II типа. Найти значения сплайна в точках от х = 1 до точки х=1,2 с шагом х = 0,01. Получить оценку точности сплайн-интерполяции и сравнить ее с фактической погрешностью вычислений.

Вариант	1	2	3	4	5	6	7	8
Функция	e x	e –x	sh x	ch x	sin x	cos x	ln x	1/x

Вариант	9	10	11	12	13	14	15	16
Функция	e 2x	e –2x	sh 1,5x	ch 2x	sin 2x	cos 2x	ln 2x	2/x

Вариант	17	18	19	20	21	22	23	24
Функция	e 3x	e –3x	sh 3x	ch 3x	sin 3x	cos 3x	ln 3x	3/x

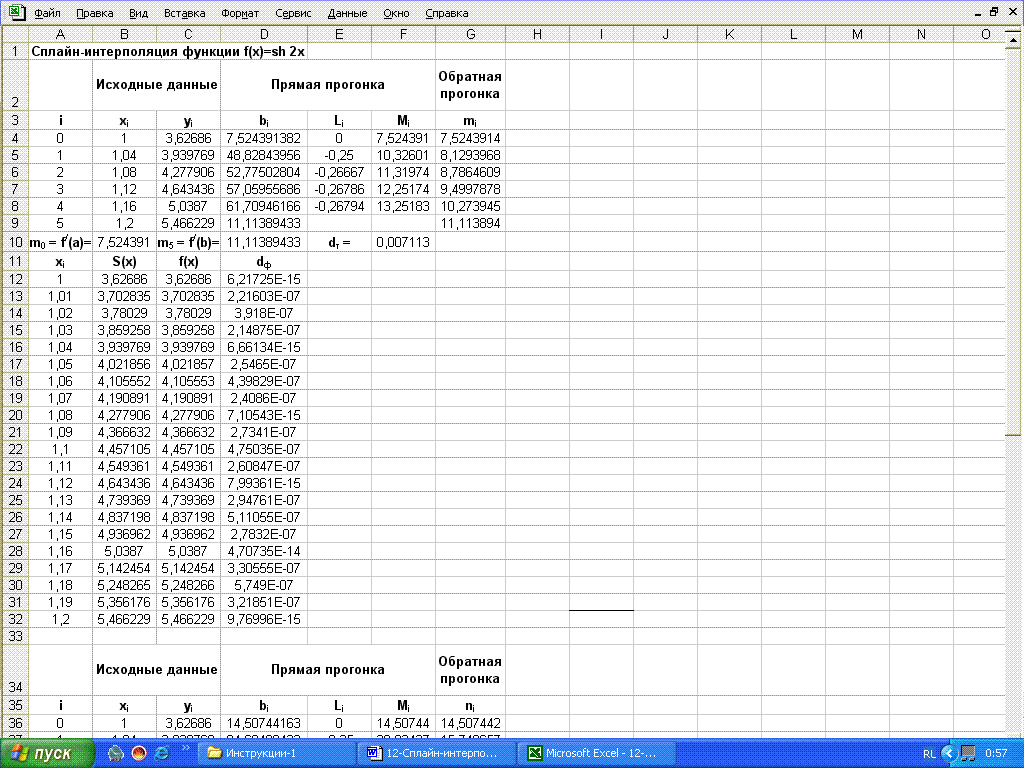
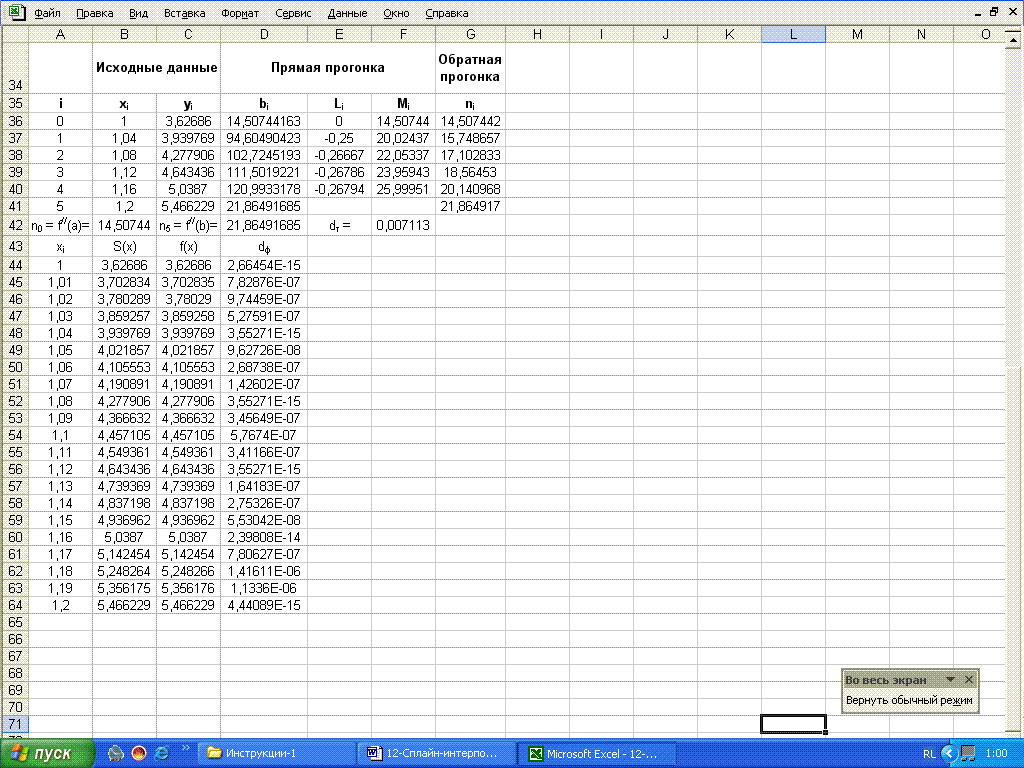
Вид расчетного листа MS Excel.

Лабораторная работа № 13

"Численное дифференцирование"

Элементы теории.

Пусть отрезок [a, b] разбит на n равных частей точками x_i : a = x₀ < x₁ < x₂ < … < x_n = b. Разность между соседними значениями аргумента постоянна, то есть шаг h = x_i – x_i-1 = const ( i = 1, 2, … , n). Пусть на отрезке [a, b] определена функция y = f(x), значения которой в точках x_i равны y_i = f(x_i).

Первая производная функции в точке x_i с помощью отношения конечных разностей выражается следующим образом:

а) аппроксимация с помощью разностей вперед (правых разностей):

...xми на ок и.ные аппроксимации производных"

000000000000000000000000000000000000000000000000000000000000000000000000000000000

, (1)

б) аппроксимация с помощью разностей назад (левых разностей):

...xми на ок и.ные аппроксимации производных"

000000000000000000000000000000000000000000000000000000000000000000000000000000000

, (2)

в) аппроксимация с помощью центральных разностей:

...xми на ок и.ные аппроксимации производных"

000000000000000000000000000000000000000000000000000000000000000000000000000000000

. (3)

Аппроксимация производных с помощью центральных разностей представляет собой среднее арифметическое соотношений (1) и (2) в точках x_i , i = 1, … , n-1. Соотношения (1) и (3) не позволяют вычислить производную в точке x_n = b, а (2) и (3) - в точке x₀ = а. Можно показать, что для функции y = f(x), имеющей непрерывную производную до второго порядка включительно, погрешность аппроксимации производных разностями вперед и назад имеет один и тот же порядок O(h), а погрешность аппроксимации центральными разностями (3) для функции y = f(x), имеющей непрерывную производную до третьего порядка включительно, имеет порядок O(h²).

Приближенное значение производной второго порядка в точке x_i выразим через значения функции y_i-1 , y_i , y_i+1 .Для этого представим вторую производную с помощью правой разности:

,

а производные первого порядка и - с помощью левых разностей:

и окончательно получим

. (4)

Погрешность последней аппроксимации имеет порядок O(h²) для функции y = f(x), имеющей непрерывную производную до четвертого порядка включительно на отрезке [a, b]. Данная формула позволяет вычислять значения второй производной только во внутренних точках отрезка.

Пусть функция y = f(x) определена на отрезке [a, b] и точках x_i , i = 0, 1, …, n принимает значения y_i = f(x_i). Разность между соседними значениями аргумента x_i постоянна и является шагом h = x_i – x_i-1 , i = 1, …, n разбиения отрезка на n частей, причем a = x₀ , b = x_n .

Найдем аппроксимации 1-го и 2-го порядков с помощью значений функции y_i в узловых точках x_i с погрешностью одного и того же порядка в зависимости от шага h, причем этот порядок не ниже, чем достигаемый при конечно-разностной аппроксимации производных для того же шага. Для того, чтобы выразить значения производных через значения функции y_i в узлах интерполяции x_i , построим интерполяционный многочлен Лагранжа L_m(x) степени m, удовлетворяющий условиям:

L_m(x_k) = f(x_k) = y_k , k = i, i+1, … , i+m, i+m  n.

Многочлен L_m(x) интерполирует функцию f(x) на отрезке [x_i , x_i+m ]. Дифференцируя многочлен L_m(x), получаем значения производных в точках x_k , k = i, i+1, … , i+m.

Если m = 1, то L₁(x) – линейная функция, график которой проходит через точки (x_i , y_i ) и (x_i+1 , y_i+1 ). Тогда

,

.

Если m = 2, то график интерполяционного многочлена Лагранжа L₂(x) – парабола, проходящая через три точки (x_i , y_i ), (x_i+1 , y_i+1 ), (x_i+2 , y_i+2 ). Вычислим 1-ю и 2-ю производные многочлена L₂(x) на отрезке [x_i , x_i+2 ]:

.

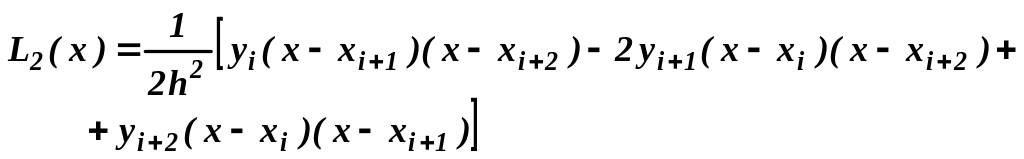
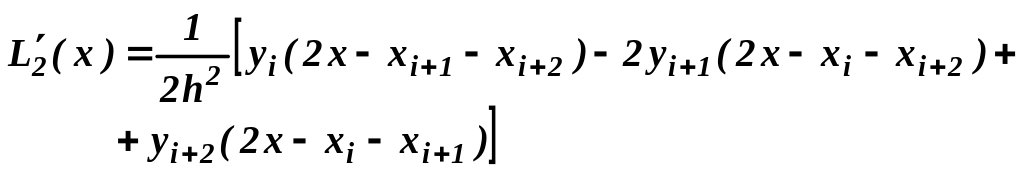
Первая и вторая производные многочлена Лагранжа L₂(x) в точках x_i , x_i+1, x_i+2 являются приближениями соответствующих производных функции f(x) в этих точках:

,

, (5)

,

. (6)

Если функция f(x) на отрезке [x_i , x_i+2 ] имеет непрерывную производную до третьего порядка включительно, то справедливо представление функции в виде суммы:

f(x) = L₂ (x) + R₂ (x), (7)

где R₂ (x) – остаточный член интерполяционной формулы, равный:

.

Дифференцируем (7):

, (8)

. (9)

Здесь:

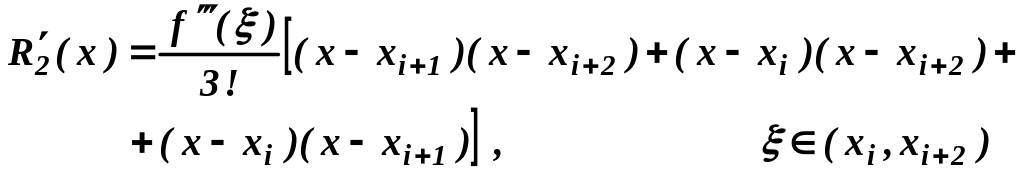(10)

. (11)

Погрешности при вычислении производных в точках x_i , x_i+1, x_i+2 определяются из формул (10)-(11) следующими значениями остатков:

, (12)

. (13)

Таким образом, равенства (12) показывают, что погрешности аппроксимации 1-й производной с помощью формул (5) имеют один и тот же порядок O(h²), и предлагается следующая рекомендация по их применению на отрезке [a, b] в точках x_i , i = 0, 1, …, n при n  2:

,

, (14)

.

Оценка погрешности вычисления первой производной производится по формулам:

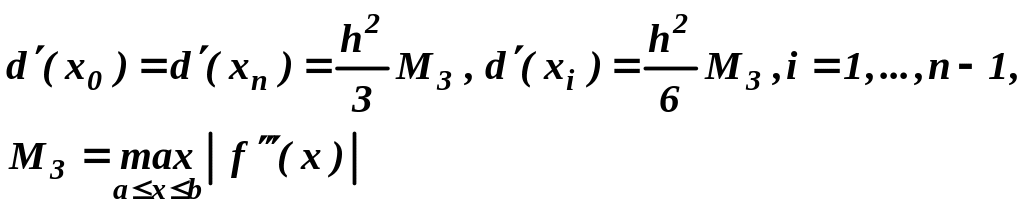. (15)

Из равенств (13) следует, что приближение второй производной с помощью формулы (6) имеет различный порядок в зависимости от h в разных точках: в точках x_i , x_i+2 имеется погрешность порядка h, а в точке x_i+1 порядок погрешности выше, так как .

В случае интерполяции функции f(x), имеющей на отрезке [a, b] непрерывную производную до четвертого порядка включительно, можно получить погрешность интерполяции второй производной, имеющую порядок h² и одинаковую во всех точках, с помощью многочлена Лагранжа третьей степени L₃(x) по четырем узлам интерполяции x_k , k = i, i+1, i+2, i+3. Аппроксимация второй производной в этом случае имеет вид:

,

,

, (16)

.

При вычислении производной второго порядка на отрезке [a, b] в точках x_i , i = 0, 1, …, n при n  3 используются формулы:

,

, (17)

.

Если функция f(x) на отрезке [x_i , x_i+m ] имеет непрерывную производную до (m+1)-го порядка включительно, то справедливо представление функции в виде:

f(x) = L_m (x) + R_m (x),

где L_m (x) – интерполяционный многочлен Лагранжа степени m, аппроксимирующий функцию f(x) по узлам интерполяции x_k , k = i, i+1, … , i+m , R_m (x) – остаточный член интерполяционной формулы, причем:

В частности, для интерполяционного многочлена Лагранжа L₃ (x) степени 3 остаточный член R₃ (x) имеет вид:

. (18)

Дважды продифференцируем R₃ (x):

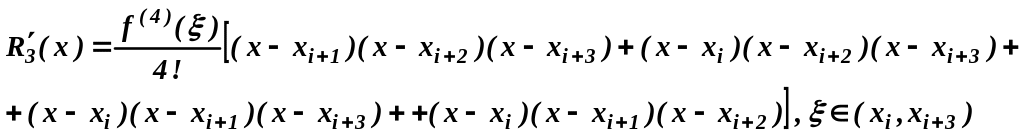
(19)

Погрешности при вычислении вторых производных в точках x_i , x_i+1, x_i+2 , x_i+3 , определяются из формулы (19) следующими значениями остатков:

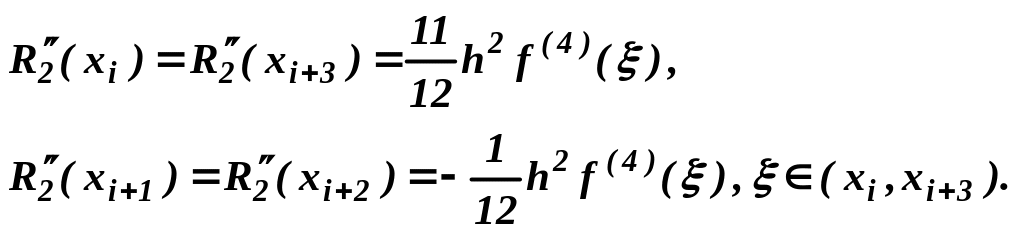(20)

Тогда оценка погрешности вычисления второй производной по формулам (17) имеет вид:

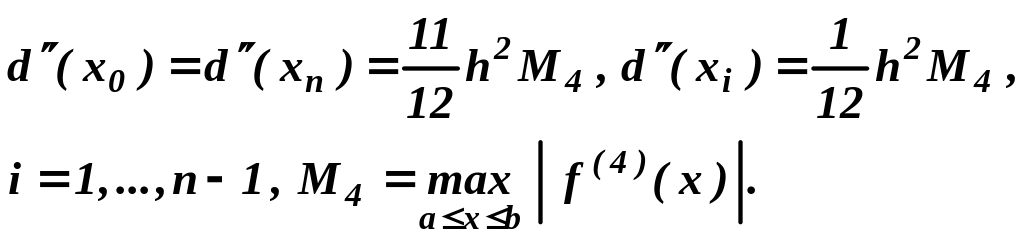(21)