Варианты.

Для заданных функций построить интерполяционный многочлен Лагранжа на отрезке [1; 1,2 ] по системе 3-х и 5-и равноотстоящих точек и вычислить его значения на отрезке [1; 1,2 ] с шагом х = 0,01. Оценить в этих точках погрешность расчета, вычислить точные значения функции f(x) и определить фактическую погрешность.

Вариант	1	2	3	4	5	6	7	8
Функция	e x	e –x	sh x	ch x	sin x	cos x	ln x	1/x

Вариант	9	10	11	12	13	14	15	16
Функция	e 2x	e –2x	sh 1,5x	ch 2x	sin 2x	cos 2x	ln 2x	2/x

Вариант	17	18	19	20	21	22	23	24
Функция	e 3x	e –3x	sh 3x	ch 3x	sin 3x	cos 3x	ln 3x	3/x

Вид рабочего листа MS Excel.

Лабораторная работа № 12

"Сплайн-интерполяция"

Элементы теории.

Пусть отрезок [a, b] разбит на n частей точками x_i : a = x₀ < x₁ < x₂ < … < x_n = b. Сплайном k-ой степени называется функция, представляющая собой многочлен k-ой степени на каждом из последовательно примыкающих друг к другу интервалов (x_i-1 ; x_i ), i = 1, 2, … , n, причем в точках стыка двух интервалов x_i , i = 1, 2, … , n-1 функция непрерывна вместе со своими производными до порядка не выше k.

Пусть на отрезке [a, b] определена функция f(x), значения которой в точках x_i равны y_i = f(x_i). Задача интерполяции функции y = f(x) на отрезке [a, b] кубическим сплайном (сплайном 3-ей степени) состоит в нахождении функции S_i(x), равной многочлену 3-ей степени на каждом отрезке [x_i-1 , x_i ] , i = 1, 2, … , n, то есть

, (1)

причем значения сплайна в узлах интерполяции x_i равны соответствующим значениям заданной функции y_i и сплайн-функция непрерывна в узлах интерполяции вместе с производными 1-го и 2-го порядка:

(2)

(3)

Условия (2) дают 4n-2 линейных алгебраических уравнения для определения 4n неизвестных коэффициентов , p = 0, 1, 2, 3, i = 1, 2, … , n при соответствующих степенях х в многочленах S_i(x). Можно показать, что интерполяционный кубический сплайн для функции y = f(x) существует и является единственным, если вместе с уравнениями (2) удовлетворяется какая-либо пара дополнительных условий (краевых условий) следующего типа:

I. ,

II. .

Рассмотрим случай разбиения отрезка[a, b] на n равных частей с шагом h, для которого x₀ = a, x₁ = x₀ + h, … , x_i+1 = x_i + h, … , x_n = b и h = (b – a)/n. Рассмотрим построение интерполяционного кубического сплайна для условий I типа.

Введем величины , называемые иногда наклонами сплайна в точках (узлах) x_i , i = 1, 2, … , n.

Интерполяционный кубический сплайн вида:

(4)

удовлетворяет условиям (2) для любых m_i . Из условий (3) и краевых условий I типа можно определить n+1 параметр m_i .

Действительно, прямыми вычислениями легко проверить, что

,

.

Можно показать, что

,

.

Тогда, учитывая краевые условия I типа и условия (3), получим систему из n+1 линейных уравнений относительно неизвестных m_i :

(5)

Решение этой системы позволяет найти значения неизвестных m_i и определить интерполяционный сплайн в виде соотношений (4). Матрица коэффициентов системы (5) имеет порядок n+1 и является трехдиагональной:

.

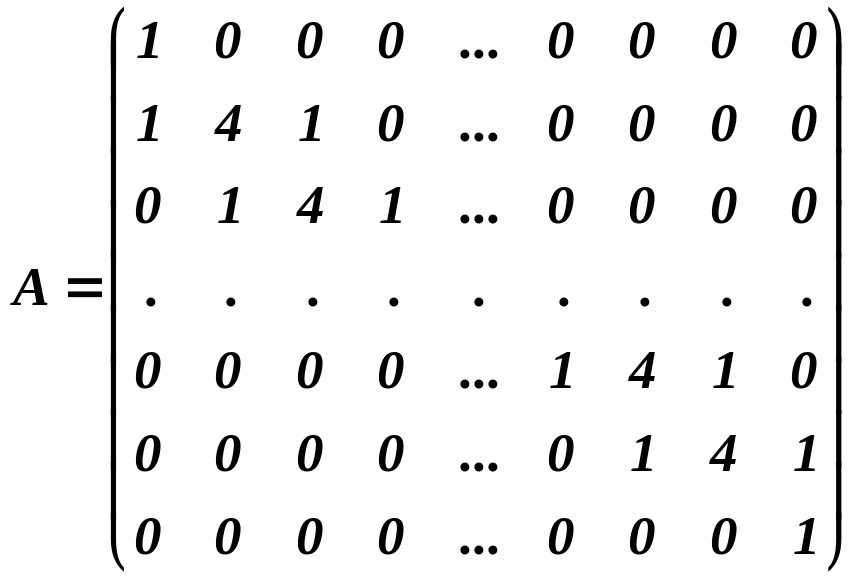Метод Гаусса (метод исключения переменных) для системы (5) значительно упрощается и носит название метода прогонки. Прямой прогонкой находят так называемые прогоночные коэффициенты:

,

Обратной прогонкой последовательно определяют неизвестные m_i :

При построении сплайна, удовлетворяющего краевым условиям II типа, введем величины - значение второй производной сплайна в узлах x_i , i = 0, 1, … , n. Уравнения (2), (3) будут удовлетворены, если интерполяционный кубический сплайн представить в виде:

, (6)

.

Учитывая, что

и используя краевые условия II типа и условия равенства производных в узлах. получим систему из n+1 линейных уравнений относительно неизвестных n_i :

(7)

Система (7), как и система (5), относятся к линейным алгебраическим системам с трехдиагональной матрицей коэффициентов и решаются методом прогонки.

Для функции f(x), имеющей на отрезке [a, b] непрерывные производные до 3-го порядка включительно, точность интерполяции ее кубическим сплайном S(x) по точкам равномерного разбиения отрезка с шагом h при любых рассмотренных краевых условиях оценивается следующим неравенством для любых х на отрезке [a, b] :

, где . (8)

Неравенство (8) дает завышенную оценку точности приближения функции сплайном в точке.