
- •Часть 2
- •Содержание
- •Введение
- •На основании теоремы для функции f(X), интегрируемой с квадратом на отрезке [-l, l], тригонометрическим многочленом наилучшего среднеквадратичного приближения является тригонометрический многочлен
- •Тригонометрический многочлен (6) с коэффициентами Фурье (7) представляет собой n-ю частичную сумму ряда Фурье, сходящегося к функции f(X) на отрезке [-l, l]:
- •Порядок выполнения лабораторной работы.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения лабораторной работы.
- •Типовой отчет.
- •Варианты.
- •Вид рабочего листа ms Excel.
- •Лабораторная работа № 14
- •Элементы теории
- •Порядок выполнения лабораторной работы.
- •Типовой отчет.
- •Варианты.
- •Вид рабочего листа ms Excel.
- •Заключение
- •Литература
- •Часть 2
На основании теоремы для функции f(X), интегрируемой с квадратом на отрезке [-l, l], тригонометрическим многочленом наилучшего среднеквадратичного приближения является тригонометрический многочлен
![]() (6)
(6)
где коэффициенты Фурье по системе тригонометрических функций для функции f(x) определяются формулами (2) и имеют вид:
 (7)
(7)
Среднеквадратичное отклонение аппроксимирующего многочлена от функции f(x), вычисляемое по формуле (3), в данном случае имеет вид:
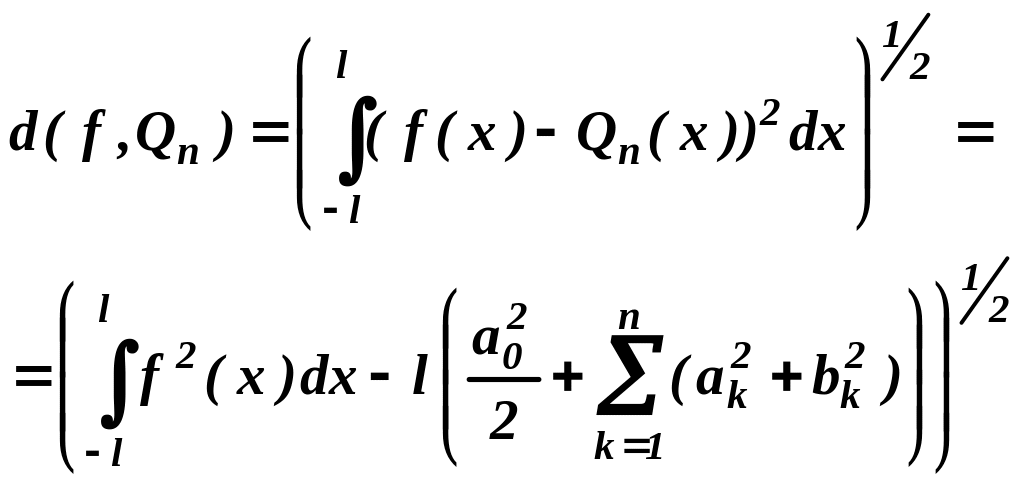 (8)
(8)
Среднеквадратичное
отклонение, отнесенное к норме
аппроксимируемой функции
![]() ,
характеризует точность приближения и
обозначается
,
характеризует точность приближения и
обозначается
![]() (9)
(9)
В частном случае, когда f(x) – четная функция на отрезке [-l, l], тригонометрический многочлен наилучшего среднеквадратичного приближения записывается в виде:
![]() ,
(10)
,
(10)
где коэффициенты Фурье
![]() (11)
(11)
Для нечетной функции f(x) на отрезке [-l, l] тригонометрический многочлен наилучшего среднеквадратичного приближения записывается в виде:
![]() ,
,
![]() (12)
(12)
Тригонометрический многочлен (6) с коэффициентами Фурье (7) представляет собой n-ю частичную сумму ряда Фурье, сходящегося к функции f(X) на отрезке [-l, l]:
![]() .
(13)
.
(13)
Порядок выполнения лабораторной работы.
Пример 1. Найти ряд Фурье для функции
![]()
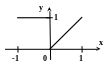 .
.
Представить графическое приближение этой функции с помощью тригонометрических многочленов степеней n = 1-5. Оценить погрешности среднеквадратического приближения.
Определяем коэффициенты Фурье:
![]() ,
,
![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
Вычислим интеграл от квадрата функции f(x) на отрезке [1, -1]:
![]() .
(14)
.
(14)
Норма функции f(x) на отрезке [1, -1]:
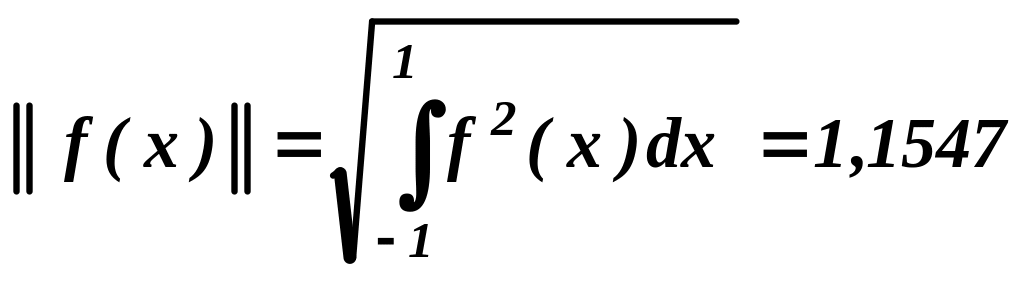 .
(15)
.
(15)
Формулы для вычисления среднеквадратических отклонений аппроксимирующих многочленов перепишем в следующем виде:
 ,
(16)
,
(16)
![]() .
(17)
.
(17)
В рассматриваемом примере l = 1.
Оформляем вычисления
в рабочем листе MS
Exsel.
Вид рабочего листа приведен на рисунке.
Фиксируем необходимые в расчетах число
,
интеграл (14) и норму (15)
: В2
= "=ПИ() ",
D2
= "1.33333",
F2
= "1.1547".
В диапазоне А3:А7
заполняем
столбец заголовков для таблицы расчета
коэффициентов Фурье. В диапазоне B3:G3
расположены
номера коэффициентов, ячейка В4
= "1.5"
(значение коэффициента а0
), С4 =
"=(COS($B$2*C3)-1)/($B$2*C3)^2" и
протяжка формулы на диапазон D4:G4
(ввод формулы
![]() ),
C5
= "=-1/$B$2/C3" и
протяжка формулы на диапазон D5:G5
(ввод формулы
),
C5
= "=-1/$B$2/C3" и
протяжка формулы на диапазон D5:G5
(ввод формулы
![]() ),
ячейка С6 =
"=КОРЕНЬ(D2-(B4^2/2+C4^2+C5^2))" (формула
(16) для
),
ячейка С6 =
"=КОРЕНЬ(D2-(B4^2/2+C4^2+C5^2))" (формула
(16) для
![]() ),
D6
= "=КОРЕНЬ(C6^2-(D4^2+D5^2))" (формула
(17) для
),
D6
= "=КОРЕНЬ(C6^2-(D4^2+D5^2))" (формула
(17) для
![]() )
и протягиваем формулу на диапазон E6:G6
(формула (17) для остальных среднеквадратичных
погрешностей
)
и протягиваем формулу на диапазон E6:G6
(формула (17) для остальных среднеквадратичных
погрешностей
![]() ),
С7 = "=C6/$F$2"
и протягиваем формулу на диапазон D7:G7
(формула (9) для точности приближений
аппроксимационных полиномов).
),
С7 = "=C6/$F$2"
и протягиваем формулу на диапазон D7:G7
(формула (9) для точности приближений
аппроксимационных полиномов).
Оформляем таблицу для вычисления значений аппроксимационных многочленов. В диапазоне В9:G9 располагаем заголовки столбцов. В диапазоне В10:В30 размещаем значения аргумента с шагом х = 0,1 на отрезке x [0, 1]. Будем использовать следующие модификации формул для вычисления значений тригонометрических многочленов (учитывая, что l = 1):
![]() ,
,
![]() .
.
Ячейка С10="=$B$4/2+($C$4*COS($B$2*B10)+$C$5*SIN($B$2 *B10))" и протяжка формулы в диапазон С10:С30 (ввод многочлена Q1), ячейка D10="=C10+(D$4*COS(D$3*$B$2*$B10)+D$5*SIN(D$3*$B$2* $B10))" и протяжка формулы в диапазон D10:G30 (ввод многочленов Qk , k = 15). На исходных данных из диапазона B9:G30 строим графики тригонометрических многочленов с помощью мастера диаграмм, используя точечную диаграмму со значениями, соединенными сглаженными значениями без маркеров, и применяя соответствующее форматирование. Толстая линия, соответствующая исследуемой функции, нанесена на чертеж от руки с помощью панели инструментов "Рисование".
Отчет к лабораторной работе должен содержать вычисление интегралов для коэффициентов Фурье и нормы заданной функции, таблицы расчета и график, приведенный на расчетом листе MS Excel.
Пример 2. Функцию
![]()
разложить в ряд Фурье по синусам. Представить графическое приближение этой функции с помощью тригонометрических многочленов степеней n1 = 1, n2 = 3, n3 = 5. Оценить погрешности среднеквадратического отклонения.
Функцию f(x) доопределим нечетным образом на промежутке [-2, 0] (см. рис.). Полученную функцию f *(x) разложим в ряд Фурье:
![]() ;
;
![]()
![]()
![]()
![]()
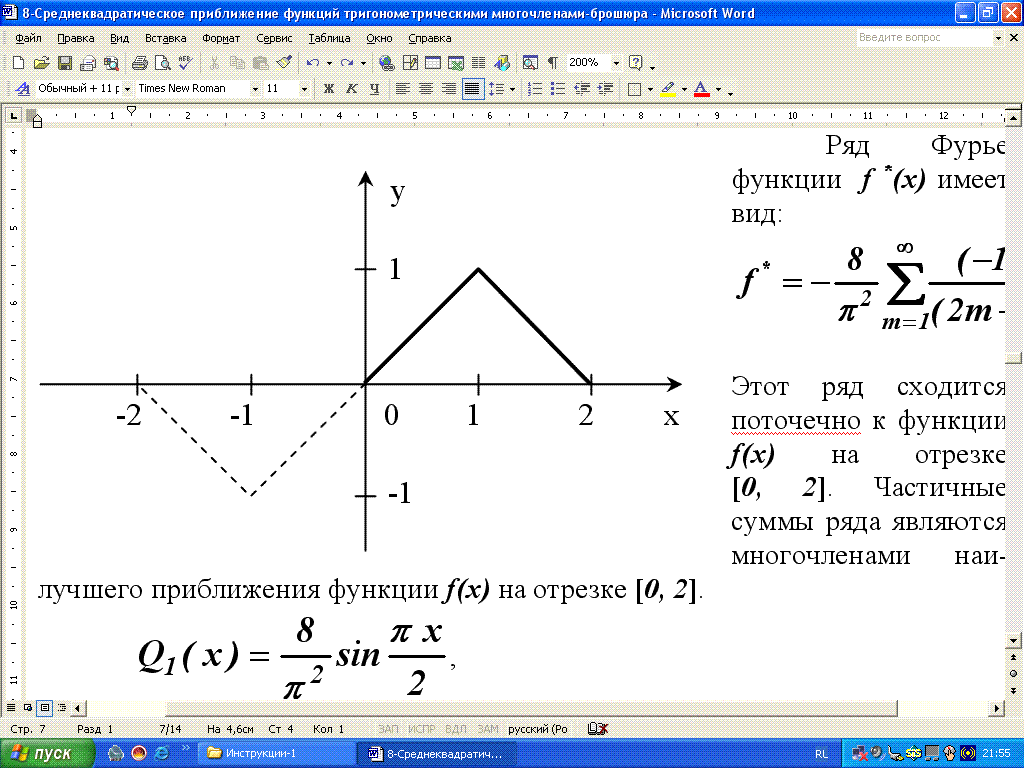
Ряд Фурье функции f *(x) имеет вид:
![]()
Этот ряд сходится поточечно к функции f(x) на отрезке [0, 2]. Частичные суммы ряда являются многочленами наилучшего приближения функции f(x) на отрезке [0, 2].
![]() ,
,
![]() ,
,
![]() .
.
![]() Вычислим
интеграл от квадрата функции f(x)
на отрезке
[0,
2]:
Вычислим
интеграл от квадрата функции f(x)
на отрезке
[0,
2]:
![]() .
.
Норма функции f(x) на отрезке [0, 2]:
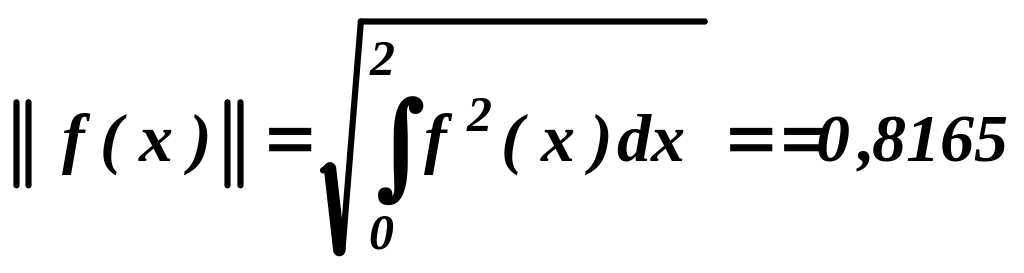 .
.
Найдем погрешность среднеквадратического приближения полиномами Q1(x), Q3(x), Q5(x) по формуле (8):
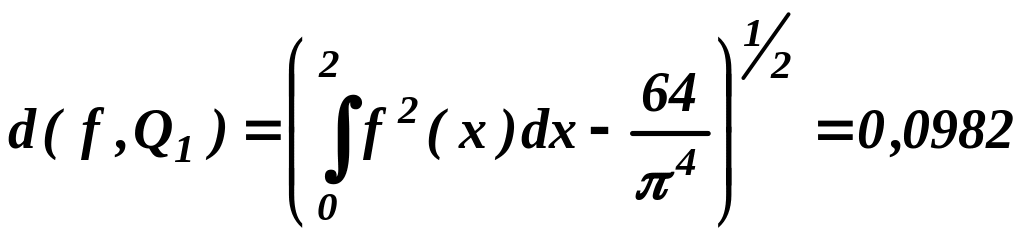 ,
,
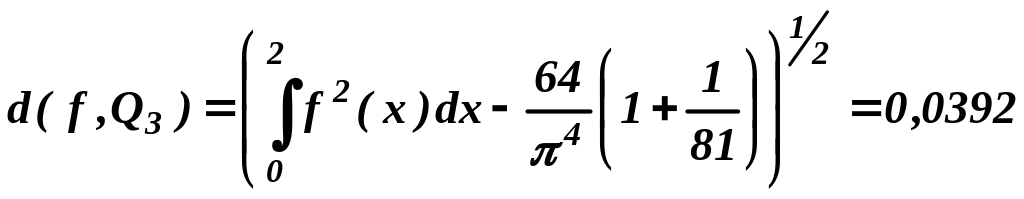 ,
,
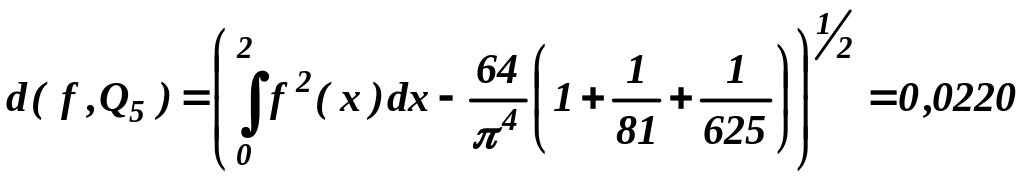 .
.
Тогда оценка точности аппроксимационных многочленов по формуле (9) равна:
![]() .
.
При аппроксимации функции, заданной на отрезке [0, l], следует изменить формулы (16)-(17) для расчета среднеквадратических отклонений аппроксимирующих многочленов:
 ,
(18)
,
(18)
![]() .
(19)
.
(19)
Остальные расчеты выполняются также, как и в примере 1. В данном примере l = 2. Результаты этого расчета в рабочем листе MS Excel приведены на рисунке.
