Министерство образования Московской области

ГОУ ВПО МО

"Коломенский государственный педагогический институт"

А.С. Трушков

ЧИСЛЕННЫЕ МЕТОДЫ

Компьютерный практикум

Часть 2

Среднеквадратическое приближение функций

Интерполяция функций

Численное дифференцирование и интегрирование

Учебное пособие

Коломна - 2006

УДК 519.613 (075.8) ББК 22.143 + 32.97 я73 Т 77

Рекомендовано к изданию редакционно- издательским советом Коломенского государственного педагогического института

Трушков А.С.

Численные методы. Компьютерный практикум. Часть 2. Среднеквадратическое приближение функций. Интерполяция функций. Численное дифференцирование и интегрирование: Учебное пособие. – Коломна: КГПИ, 2006 – 92 с.

Данное учебное пособие предназначено для выполнения компьютерного практикума по дисциплине "Численные методы" для студентов физико-математических факультетов педагогических вузов. Во второй части учебного пособия рассмотрены лабораторные работы по интегральному и точечному среднеквадратическому приближению функций, интерполяции функций многочленами Лагранжа и кубическими сплайнами, численному дифференцированию и интегрированию.

Рецензенты:	Новиков В.Г., доктор технических наук, профессор, начальник сектора Конструкторского бюро машиностроения
	Родионов К.А., кандидат технических наук, доцент кафедры информационных технологий Коломенского института Московского государственного открытого университета

 ГОУ ВПО МО "КГПИ", 2006

 Трушков А.С., 2006

Содержание

Введение ……………………………………………………………………	4
Лабораторная работа № 8 "Интегральное среднеквадратическое приближение функций тригонометрическими многочленами" ….	5
Лабораторная работа № 9 "Точечное среднеквадратичное приближение функций"…………………….................................................	16
Лабораторная работа № 10 "Метод наименьших квадратов" …………...	27
Лабораторная работа № 11 "Интерполяционная формула Лагранжа" …	44
Лабораторная работа № 12 "Сплайн-интерполяция" …………………….	51
Лабораторная работа № 13 "Численное дифференцирование" …………	64
Лабораторная работа № 14 “Численное интегрирование" ………………	74
Заключение …………………………………………………………………	90
Литература ………………………………………………………………….	91

Введение

Данное учебное пособие написано в соответствии с программой по дисциплине "Численные методы", изучаемой студентами физико-математических факультетов педагогических вузов. Во второй части учебного пособия представлены материалы 7 лабораторных работ, которые охватывают следующие разделы программы:

- среднеквадратичная аппроксимация аналитических и табличных функций;

- интерполяция функций;

- численное дифференцирование;

- численное интегрирование.

В каждом разделе приводятся необходимые теоретические сведения: основные теоремы, определения, формулы, определения и т.д. Кроме того, в каждом разделе приведен пример решения соответствующей задачи с использованием табличного процессора MS Excel.

В лабораторной работе № 8 "Интегральное среднеквадратическое приближение функций тригонометрическими многочленами" производится аналитическое вычисление коэффициентов Фурье, строятся тригонометрические многочлены соответствующих степеней, производится вычисление точности приближений. В лабораторной работе № 9 "Точечное среднеквадратичное приближение функций" аппроксимация табличных данных производится с помощью многочленов Чебышева. В лабораторной работе № 10 решается задача сглаживания экспериментальных данных эмпирической кривой с помощью метода наименьших квадратов. Интерполяция данных многочленами Лагранжа и сплайнами 3-го порядка рассмотрены в лабораторных работах № 11 и № 12. В лабораторной работе № 13 производится численное определение производных первого и второго порядков на основе аппроксимаций 2-го порядка точности. В лабораторной работе № 14 вычисление определенных интегралов производится с помощью методов прямоугольников, трапеций, Симпсона и Гаусса.

Лабораторная работа № 8

"Интегральное среднеквадратическое приближение

функций тригонометрическими многочленами"

Элементы теории

Пусть на отрезке [a, b] задана функция f(x) и определена система функций g_k(x), k = 0, 1, 2, … Обобщенным многочленом (полиномом) порядка n относительно системы функций g_k(x) называют функцию вида:

,

где С₀ , С₁ , …, С_n – некоторые постоянные.

Обобщенный многочлен Q_n(x) называют многочленом наилучшего среднеквадратичного приближения функции f(x) на отрезке [a, b], если расстояние от многочлена до функции f(x) по среднеквадратичной норме наименьшее:

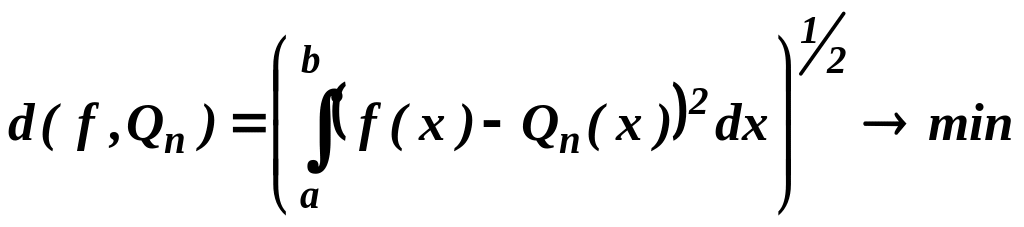. (1)

Таким образом, сформулирована задача об интегральном среднеквадратичном приближении (аппроксимации) функции f(x) на отрезке [a, b] обобщенным многочленом, которая сводится к выбору коэффициентов С₀ , С₁ , …, С_n из условия (1).

Задача нахождения многочлена наилучшего приближения Q_n(x) функции f(x) на отрезке [a, b] упрощается, если система функций g_k(x) обладает свойством ортогональности на отрезке [a, b].

Скалярным произведением функций g_i(x) и g_j(x) на отрезке [a, b] называется интеграл от их произведения на этом отрезке:

.

Число 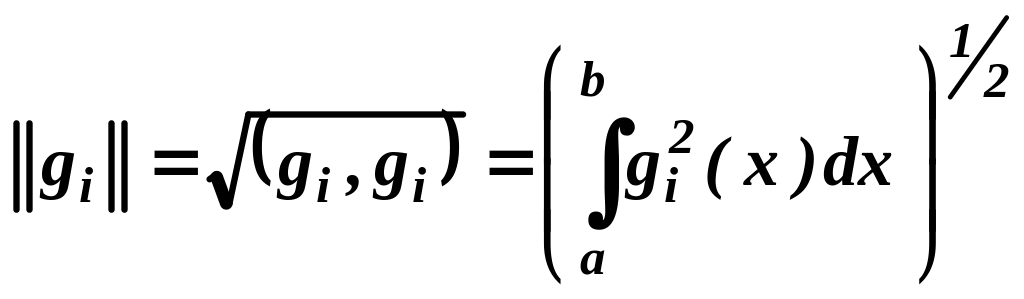является нормой функции g_i(x) на отрезке [a, b], а функция f(x), для которой существует интеграл , называется интегрируемой с квадратом на отрезке [a, b].

Функции g_i(x) и g_j(x) называется ортогональными на отрезке [a, b], если их скалярное произведение на этом отрезке равно нулю:

.

Система функций g_k(x) называется ортогональной на отрезке [a, b], если все функции этой системы попарно ортогональны на этом отрезке.

Коэффициенты С₀ , С₁ , …, С_n обобщенного многочлена называются коэффициентами Фурье функции f(x) относительно системы функций g_k(x), если они определяются по формулам:

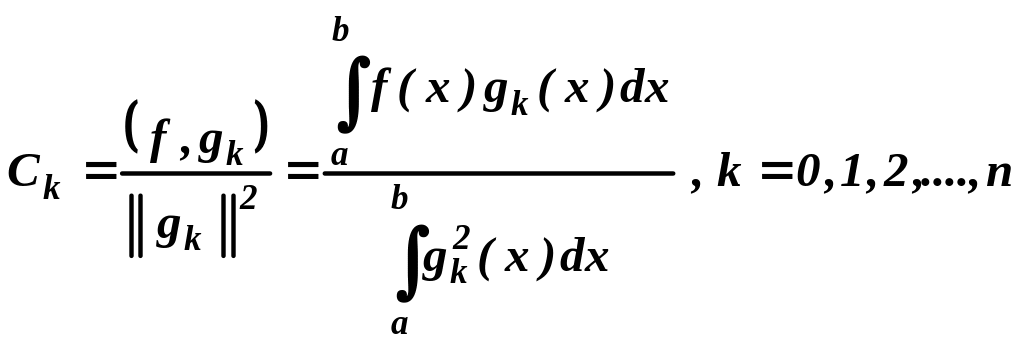. (2)

Теорема. Для любой функции f(x), интегрируемой с квадратом на отрезке [a, b], обобщенный многочлен n-го порядка Q_n(x) с коэффициентами Фурье функции f(x) относительно ортогональной на отрезке [a, b] системы функций g_k(x), k = 1, 2, … является многочленом наилучшего среднеквадратичного приближения этой функции, причем квадрат наименьшего среднеквадратичного отклонения определяется соотношением:

, (3)

где С_k – коэффициенты Фурье, вычисленные по формуле (2).

Из (3) видно, что с увеличением порядка обобщенного многочлена среднеквадратичное отклонение не увеличивается.

Пусть задана система тригонометрических функций на отрезке [-l, l]:

(4)

Тригонометрическим многочленом n-ой степени называют обобщенный многочлен по системе тригонометрических функций, имеющий вид:

, (5)

где С₀ , С₁ , … , С_n , D₁ … , D_n – некоторые числа.

Система тригонометрических функций ортогональна на отрезке [-l, l].