Вид рабочего листа ms Excel.

00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Лабораторная работа № 14

“Численное интегрирование"

Элементы теории

Для приближенного вычисления определенного интеграла разобьем отрезок интегрирования [a, b] на n равных частей точками x₀ = a, x₁ = x₀ + h, … , x_i+1 = x_i + h, … , x_n = b (h = (b – a)/n – шаг интегрирования). Значения функции f(x) в точках разбиения x_i обозначим через y_i . Непрерывная подынтегральная функция y = f(x) заменяется сплайном – кусочно-полиноминальной функцией S(x) , аппроксимирующей данную функцию. Интегрируя функцию S(x) на отрезке [a, b] , придем к некоторой формуле численного интегрирования (квадратурной формуле). В зависимости от функции S(x) , аппроксимирующей подынтегральную функцию, будем получать различные квадратурные формулы.

Если на каждой части [x_i-1 , x_i] , i = 1, 2, … , n деления отрезка [a, b] функцию f(x) заменить функцией, принимающей постоянное значение, равное, например, значению функции f(x) в серединной точке i-ой части , то функция S(x) будет иметь ступенчатый вид:

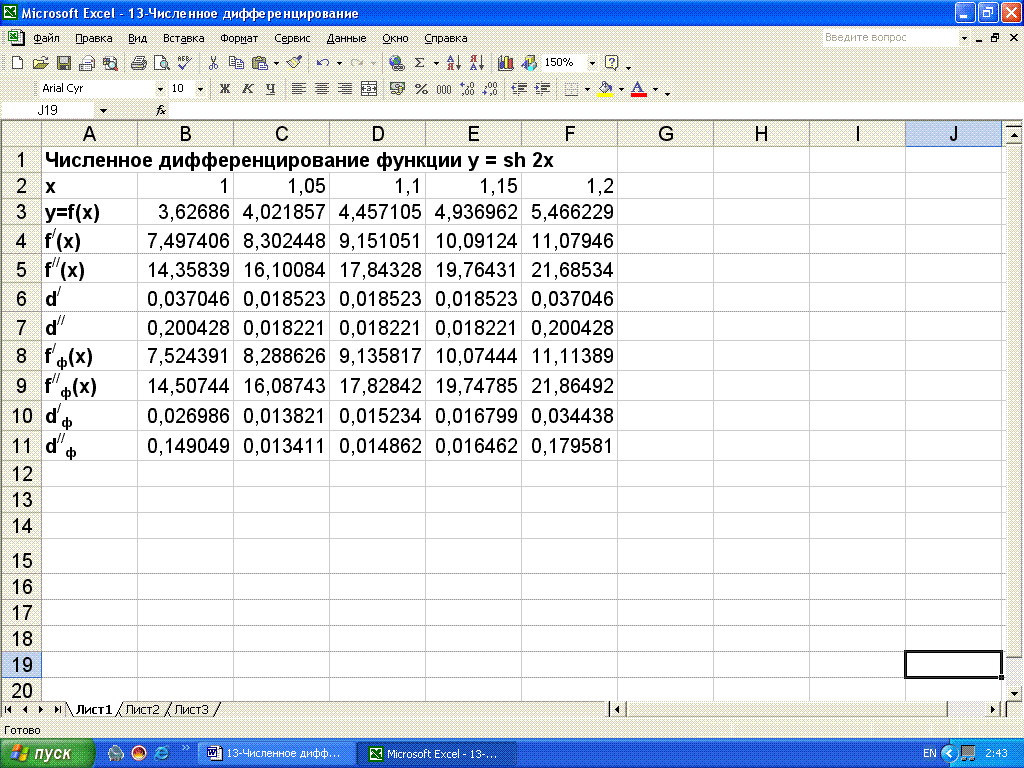
S(x) = S _i(x) = y_i-1/2 = f(x_i-1/2 ), x  [x_i-1 , x_i] , i = 1, 2, … , n .

В этом случае

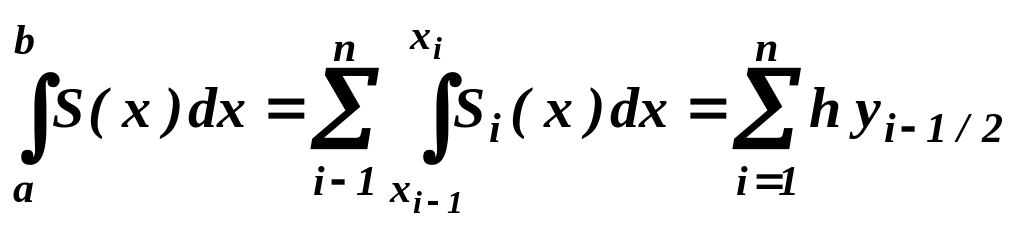
и получим квадратурную формулу прямоугольников:

. (1)

Если функцию f(x) на каждом отрезке [x_i-1 , x_i] заменить ее линейной интерполяцией по точкам (x_i-1 , y_i-1 ) и (x_i , y_i ), то получим непрерывную кусочно-линейную функцию

.

В этом случае

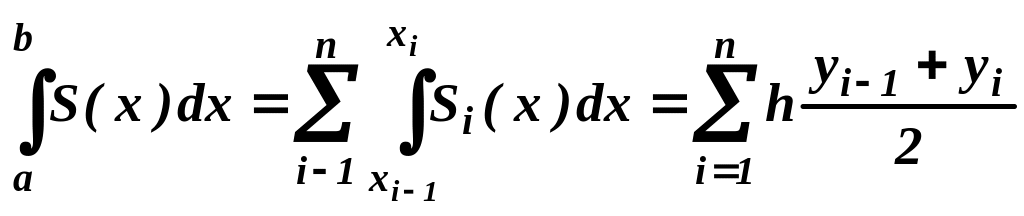
и получаем квадратурную формулу трапеций:

. (2)

Можно получить квадратурную формулу Симпсона, называемую так же формулой парабол, если сплайн S(x), аппроксимирующий подынтегральную функцию f(x), представляет собой непрерывную функцию, составленную из примыкающих парабол. Потребуем, чтобы на отрезке [x_i-1 , x_i] парабола проходила через точки (x_i-1 , y_i-1 ), (x_i-1/2 , y_i-1/2 ), (x_i , y_i ). Используя построение интерполяционного многочлена Лагранжа второго порядка на отрезке [x_i-1 , x_i], получим сплайн

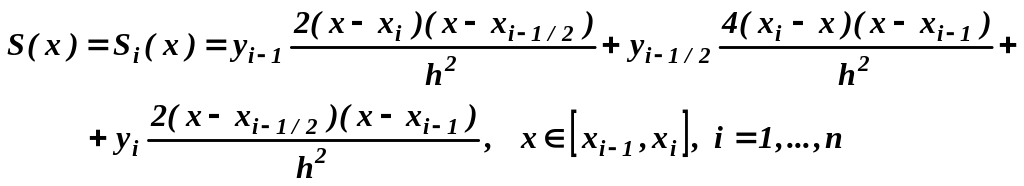
Можно показать, что после интегрирования приходим к квадратурной формуле парабол:

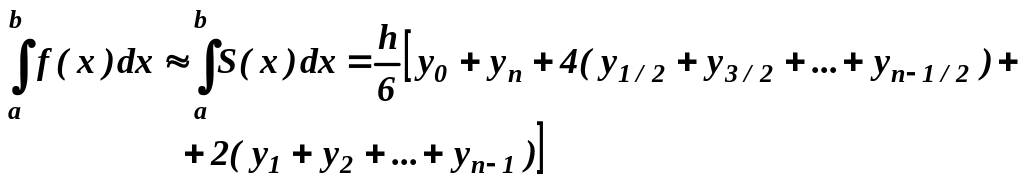(3)

Приближенное значение интеграла J_параб , вычисленное по квадратурной формуле парабол, можно выразить через значения J_прям и J_трап - результаты вычислений по квадратурным формулам прямоугольников и трапеций:

.

Погрешность каждой квадратурной формулы оценивается величиной остаточного члена R(h), зависящего от шага разбиения h:

.

Оценки погрешностей квадратурных формул в том случае, когда подынтегральная функция имеет непрерывную производную второго порядка, имеют вид:

для формулы прямоугольников:

;

для формулы трапеций:

.

Если подынтегральная функция имеет непрерывную производную четвертого порядка, то справедлива следующая оценка погрешности формулы Симпсона:

.

При интегрировании степенной функции, степень которой не выше трех квадратурная формула Симпсона дает точный результат.

Практически важно вести вычисления до достижения заданной точности  по той или иной квадратурной формуле. Этой цели удовлетворяет метод двойного пересчета. По квадратурной формуле проводят вычисление интеграла с шагом h и получают значение J(h). Затем уменьшают шаг вдвое и получают новое приближенное значение интеграла J(h/2). Чтобы определить, как сильно уклоняется значение J(h/2) от точного значения интеграла J, используется правило Рунге:

, (4)

где k = 2 для формул прямоугольников и трапеций и k = 4 для формулы Симпсона.

При заданной точности  вычисления с уменьшающимся шагом проводят до выполнения условия:

.

При этом полагают J  J(h/2) с точностью  .

Пусть отрезок интегрирования [a, b] непрерывной функции f(x) разбит на n равных частей точками x₀ = a, x₁ = x₀ + h, … , x_i+1 = x_i + h, … , x_n = b (h = (b – a)/n – шаг интегрирования). Обозначим S(x) – сплайн-функцию, аппроксимирующую подынтегральную функцию f(x). Пусть на каждой части разбиения [x_i-1 , x_i] , i = 1, 2, … , n расположено m узлов (x_i1 , x_i2 , … , x_im ), в которых подынтегральная функция принимает значения f(x_ij), j = 1, … , m. Предположим, что функция на каждой i-ой части аппроксимируется многочленом S_i(x) степени р, x  [x_i-1 , x_i], i =1, … , n. При этом на многочлен S_i(x) накладываются два ограничения:

а) значения многочлена и подынтегральной функции равны в узлах интерполяции, т. е. S_i(x_ij) = f(x_ij), i =1, … , n, j = 1, … , m;

б) определенный интеграл от функции S_i(x) на отрезке [x_i-1 , x_i] выражается через значения подынтегральной функции f(x_ij) в узлах в виде их линейной комбинации:

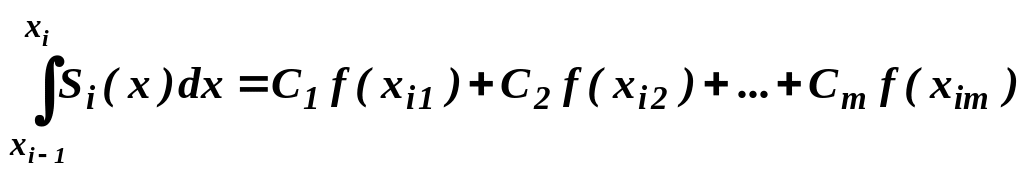. (5)

Квадратурные формулы Гаусса для выбранной степени р сплайна будут определены, если из условий а) и б) удастся найти m неизвестных коэффициентов C_j и координаты m узлов x_ij .

Можно показать, что при m = 3 координаты узлов равны:

, (6)

а квадратурная формула Гаусса записывается в виде:

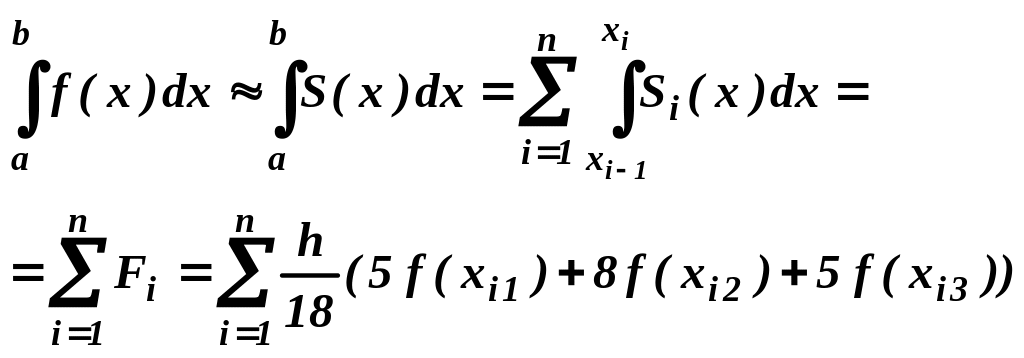(7)

Если подынтегральная функция имеет непрерывную производную шестого порядка, то для оценки погрешности формулы Гаусса с тремя узлами можно использовать неравенство:

.

При вычислении интеграла до достижения заданной точности  методом двойного пересчета условие окончания вычислений имеет вид:

, (8)

где k = 2m, m – число узлов в квадратурной формуле Гаусса. Полагают, что J  J(h/2) с точностью  .