2.6. Линейные модели и характеристики систем управления.

Модели ВХОД-ВЫХОД. Основными формами представления операторов преобразования входных переменных f(t) в переменные выхода у(t) являют-ся дифференциальные уравнения, передаточные функции, временные и час- тотные характеристики. Для одномерных систем переменные f(t) и у(t) яв- ляются скалярами. Эти и некоторые другие представления операторов рас- сматриваемого класса моделей могут быть приняты за основу задания дина- мических свойств в терминах вход-выход. Если для конкретных исследова-

ний та или иная форма оказывается более предпочтительной, ставится и ре-

шается и решается задача перехода от одной формы к другой например, пос-

троение временных и частотных характеристик по дифференциальному ура-

внению или передаточной функции.

Обыкновенное линейное дифференциальное уравнение n-го порядка с пос-

тоянными коэффициентами имеет вид:

a_ndⁿу/dtⁿ + …. + a₁dу/dt + a_oу = b_md^mf/dt^m + ….. + b₁df/dt + b_of (2 – 14)

Если ввести оператор дифференцирования по времени р  d/dt, то уравне- ние (2-14) запишется в компактной форме

А(р) у(t) = В(р) f(t) , (2 – 15)

где А(р) = a_npⁿ + …. +a₁p + a_o ; В(р) = b_mp^m + …. +b₁p + b_o – операторные по-

линомы. Дифференциальное уравнение дополняется начальными условиями у(0), у’(0), … , у^(n-1)(0).

Передаточная функция равна отношению изображений по Лапласу перемен-

ных выхода и входа при нулевых начальных условиях W(s) = У(s)/F(s) , где

интегральное преобразование Лапласа определяется так:

У(s) = L{у(t)} = у(t) е ^–stdt;

F(s) = L{f(t)} = f(t) e ^–st dt

Преобразуя дифференциальное уравнение (2-14) при начальных условиях,

получим алгебраическое уравнение для изображений

А(s) У(s) = B(s) F(s).

Отсюда следует, что передаточная функция легко записывается по диффере-

нциальному уравнению W(s) = B(s) / A(s) (2 – 16)

и наоборот, по передаточной функции сразу записывается дифференциальное

уравнение.

Зная передаточную функцию и изображение переменной входа, легко найти

изображение выхода У(s) = W(s) F(s).

Временные характеристики.

Временные характеристики являются одной из форм представления операто-

ров преобразования переменной f(t) в переменную у(t).

Импульсная переходная функция или функция веса w(t) – реакция системы

на единичный идеальный импульс (t) при нулевых начальных условиях. Пе-

ременная выхода определяется как интервал свертки

у(t) = w(t) f(t-)dt , (2 – 17)

т.е. в этом случае оператор преобразования имеет форму интегрального урав-

нения.

Другая, часто употребляемая временная характеристика – переходная харак-

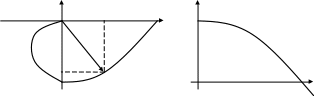
теристика h(t) – реакция системы на единичную ступенчатую функцию 1(t) при нулевых начальных условиях. На рис.2.15 представлен примерный вид временных характеристик для системы второго порядка.

w h

0 t 0 t

а) б)

Рис.2.15. Временные характеристики: а) функция веса;

б) переходная характеристика

Частотные характеристики.

Частотные характеристики элементов и систем представляют собой зависи-

мость параметров установившихся реакций на гармонические сигналы всех частот и единичных амплитуд. В линейных системах форма и частота устано-

вившейся реакции совпадают с формой и частотой сигнала на выходе. Комп-

лекная частотная характеристика W(j) дает возможность определить ампли-

туду R() и фазу  () гармонического сигнала на выходе системы по значе-

нию частоты: W(j) = R() e ^j() = P() + JQ() , (2 – 18)

где R() = mod W(j) и  () = arg W(j) – амплитудная и фазовая частот-

ные характеристики, а P() = Re W(j) и Q() = Im W(j) – вещественная и

мнимая частотные характеристики. На рис.2.16. приведен пример годографа

W(j), называемого амплитудно-фазовой характеристикой (АФХ).

Реальные объекты с повышением частоты хуже пропускают сигналы – ос-

лабляют амплитуду и вносят отрицательный фазовый сдвиг.

L

 = ∞ Р()  = 0

- 20

 ()

W(j)

R() - 40

Q() ()



Рис.2.16. Пример AФХ Рис.2.17. Пример ЛАЧХ

Амплитудно-частотные характеристики удобно представлять в логарифми-

ческом масштабе L() = 20lgR().

Если частота изменяется в логарифмическом масштабе, то логарифмичес-

кие амплитудно-частотные характеристики (ЛАЧХ) во многих практически

важных случаях мало отличаются от прямолинейных асимптот с наклонами,

кратными 20дБ/дек.

На рис.2.17. представлен примерный вид асимптотической ЛАЧХ; пунктир-

ная линия – точная ЛАЧХ, а также указаны наклоны асимптот в дБ/дек.

Передаточные функции, все нули и полюсы которых находятся в левой полу-

плоскости, называют минимально-фазовыми. Такие передаточные функции соответствуют меньшим по модулю фазовым сдвигам по сравнению с любы-

ми другими передаточными функциями, имеющими ту же ЛАЧХ, но часть нулей и/или полюсов справа от минимальной оси.

Преобразование форм представления моделей вход-выход.

Известно, что любая из форм представления операторов может быть приня-

та за основу задания динамических свойств систем, для конкретных исследо-

ваний, так как та или иная форма оказывается более рациональной. Возника-

ет необходимость перехода от одной формы к другой. Многие задачи анализа связаны с преобразованием формы представления оператора. В ряде случаев

эта процедура составляет наиболее трудоемкий этап анализа – построения частной модели – приведение к форме, позволяющей непосредственно вычи-

слять показатели качества и вывести суждение о соответствии поведения сис-

темы заданным требованиям (например, построение временных или частот-

ных характеристик системы управления).

Переходы между различными формами представления операторов следует

рассматривать как дуги орграфа, вершинам которого соответствуют формы представления, как приведено на рис.2.18.

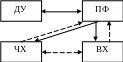Рис.2.18. Орграф взаимосвязи

форм представления операторов:

ДУ-дифференциальное уравнение;

ЧХ – частотные характеристики;

ПФ – передаточная функция;

ВХ – временная характеристика.

Наиболее прост формальный переход путем замены оператора дифференци-

рования р  d/dt на комплексный аргумент (s) от дифференциального уравне-

ния (2-15) к передаточной функции (2-16) и обратно. Осуществляя переход к передаточным функциям, необходимо избегать сокращения общих делителей

полиномов числителей и знаменателей, т.е. диполей рациональных функций.

Такое сокращение приводит к потере части собственных составляющих дви-

жения при нулевых предначальных условиях (составляющих собственных движений).

Пунктирные линии графа взаимосвязи (см. рис.2.18.) отвечают переходам,

рассматриваемым обычно в задачах идентификации. По временным и/или частотным характеристикам, полученным экспериментально, оценивают па-

раметры передаточных функций или ординаты характеристик иного типа.

Такие переходы оказываются неоднозначными, а их результаты зависят от выбора структуры оператора и алгоритма обработки данных.

Типовые звенья.

Известно, что любую систему управления можно представить в виде соеди-

нения типовых динамических звеньев.

Элементарные звенья – это простые множители, входящие в состав переда-

точной функции системы или ее части. Звено принято изображать в виде пря-

моугольника, в контур которого вписывают оператор, характеризующий ди-

намику преобразования входного сигнала в выходной. Обозначения входных, промежуточных и выходных переменных, возмущающих и управляющих воздействий записывают над линией или с правой стороны линии связи, по-

казывающей место приложения соответствующего сигнала. Промежуточные

переменные – это координаты, связывающие отдельные звенья структурной

схемы. Суммирующие элементы (сумматоры) изображают в виде круга, раз-

деленного на секторы.

При представлении модели системы в форме пространства состояний, для

реализации любой физически осуществимой передаточной функции достато-

чно двух типов звеньев: интеграторов и усилителей. Если степень числителя передаточной функции m превышает степень знаменателя n, то необходимо

звено дифференцирующего типа. Удобнее форму оператора представить в виде оператора дифференцирования рd/dt (cм. рис.2.5).

К типовым звеньям относят устойчивые элементарные звенья. Практичес-

кое применение в основном имеют нижеследующие звенья:

Вид звена Передаточная функция W(р) звена

пропорциональное (усилительное) W(p) = K

интегрирующее W(p) = 1/Тр

дифференцирующее W(p) = Кр

апериодическое (1 порядка) W(p) = К/Тр + 1

апериодическое (2 порядка) W(p) = К/Т₂² р² + Т₁р + 1

где К – коэффициент усиления; Т – постоянная времени

В теории управления состав типовых звеньев несколько расширен исходя

из соображений удобства – необходимы звенья, моделирующие часто встре-

чающие случаи, а также представления передаточных функций общего вида

последовательным и параллельным соединением типовых звеньев (например,

пропорционально-дифференцирующее звено: W(p) = K(Tp + 1).

К типовым соединениям относят последовательное, параллельное и паралле-

льно-встречное (с обратной связью) соединение звеньев. На рис.2.19. приве-

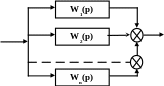
дены вышеуказанные типовые соединения звеньев.

W₁(p)

W₂(p)

W_n(p)

х₁ х₂ х_n у

а)

прямая цепь

х х-у₂ у

у у₂

х

в)

б) обратная цепь

Рис.2.19. Типовые соединения звеньев

Последовательное соединенные звенья W₁(p),……, W_n(p) можно заменить

одним звеном (рис.2.19,а) с передаточной функцией W_n(p), равной произве-

дению передаточных функций отдельных звеньев:

W(p) = W₁(p),…….., W_n(p) = W₁(p) (2 – 19)

Эквивалентная передаточная функция W_n(p) параллельно включенных зве-

ньев W₁(p),……,W_n(p) равна их сумме (рис.2.19,б):

W(p) = W₁(p) + ………. + W_n(p) = W_i(p) (2 – 20)

В соединениях с обратной связью (см. рис.2.19,в) различают прямую и об-

ратную цепи. Прямая цепь – это участок системы (схемы) по ходу передачи

сигнала от входного воздействия f к выходной координате у.