2012-аппроксимация шрифт 12

 АППРОКСИМАЦИЯ ЗАВИСИМОСТЕЙ

Excel располагает средствами, позволяющими прогнозировать процессы. Задача аппроксимации возникает в случае необходимости аналитически описать явления, имеющие место в жизни и заданные в виде таблиц, содержащих значения аргумента (аргументов) и функции.

Если зависимость удается найти, можно сделать прогноз о поведении исследуемой системы в будущем и, возможно, выбрать оптимальное направление ее развития. Такая аналитическая функция (называемая еще трендом) может иметь разный вид и разный уровень сложности в зависимости от сложности системы и желаемой точности представления.

	A	B	C	D	E	F	G	H	I	J
1	Yф	2	3	6	7	8	5	4	3
2	Yп				3,7	5,3	7,0	6,7	5,7	4,0	Рис.1-1

1. Скользящее среднее. Это самый простой метод сглаживания. Он заключается в том, что прогнозное значение вычисляется как среднее арифметическое какого-то количества прошлых значений. На рис. 1-1 первая строка – это фактические значения, вторая – прогнозные. Среднее значение возьмем за три предыдущих периода (например, три года) F2=СУММ(B1:D1)/3. Первоначально известны только три точки (значения 2; 3; 6). Прогнозное значение составило Yп=3,7. По истечении 4-го года появилось новое значение (7) и мы передвинули функцию вправо. Теперь Yп=5,3 и т. д. Конечно, это очень грубый метод и он дает только одну новую точку. Постройте диаграмму для обеих строк (тип График с маркерами).

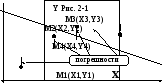
2. Линейная регрессия. Самой популярной является аппроксимация прямой – линейная регрессия. Пусть мы имеем фактическую информацию об уровнях прибыли Y в зависимости от размера X капиталовложений – Y(X). На рис. 2-1 показаны четыре такие точки М(Y,X). Пусть также у нас имеются основания полагать, что зависимость эта линейная, т.е. имеет вид Y=А+ВX. Если бы нам удалось найти коэффициенты A и B и по ним построить прямую (например, такую, как на рисунке), в дальнейшем мы могли бы сделать осознанные предположения о динамике бизнеса и возможном коммерческом состоянии предприятия в будущем. Очевидно, что нас бы устроила прямая, находящаяся как можно ближе к известным точкам М(Y,X), т.е. имеющая минимальную сумму отклонений или сумму ошибок min. На рисунке отклонения показаны пунктиром. Поскольку отклонения могут иметь разный знак, то следует искать минимум суммы их модулей min. Однако для такой функции неприменим метод поиска экстремума через приравнивание производной нулю. Производная в интересующей нас точке не берется. Поэтому применяется иной подход. Вместо используем другую функцию ², что также обеспечит нам положительность всех отклонений. Этот метод называется метод наименьших квадратов (ошибок). Известно, что существует только одна такая прямая, отвечающая критерию ²min.

Разность (ошибка) между известным значением Y₁ точки М₁(Y₁,X₁) и значением Y(X₁), вычисленным по уравнению прямой для того же значения X₁, составит

₁ = Y₁ – A – BX₁.

Такая же разность для X=X₂ будет ₂=Y₂-A-BX₂; для X₃: ₃=Y₃-A-BX₃; для X₄: ₄=Y₄-A-BX₄.

Запишем выражение для суммы квадратов этих ошибок (индексы при сумме опускаем)

Ф(A,В)=(Y₁–A–BX₁)²+(Y₂–A–BX₂)²+(Y₃–A–BX₃)²+(Y₄–A–BX₄)² или Ф(B,A)=(Yi –A–BXi)².

Здесь нам известны все X и Y и неизвестны коэффициенты A и B. Проведем искомую прямую так (т.е. выберем A и B такими), чтобы эта сумма квадратов ошибок Ф(A,B) была минимальной. Условиями минимальности являются известные соотношения

Ф(A,B)	=	0	и	Ф(A,B)	=	0
A				B

Выведем эти выражения:

	[(Yi–A–BXi)2] A	=2(Yi–A–BXi)(–1)
	[(Yi–A–BXi)2] B	=2(Yi–A–BXi)(–Xi)

Преобразуем полученные формулы и приравняем их 0

	2(–Yi +BXi+A) =0
	2(–XiYi +BXi2+AXi) =0

Сократим выражения на 2 и раскроем скобки. Тогда

	–Yi +BXi + A =0
	–XiYi) +BXi2+AXi =0

Мы получили систему из двух линейных алгебраических уравнений, в которой неизвестными являются A и B, а сумма N единиц равна N (в нашем случае 1=4). Перенесем свободные члены в правую часть и для упрощения записи опустим индексы при знаке суммирования. Окончательно получим:

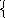
A B C D E F G 1 Уравнение регрессии 2 Y= a+bx = 1,8 +0.64x R= 0,722 3 i Xi Yi Xi*Yi X2 Yрасч. Y2 4 1 1 1 1 1 2,44 1,0 5 2 2 5 10 4 3,07 25,0 6 4 3 6 18 9 3,71 36,0 7 3 4 5 20 16 4,35 25,0 8 5 5 4 20 25 4,98 16,0 9 6 6 3 18 36 5,62 9,0 10 8 7 4 28 49 6,25 16,0 11 7 8 6 48 64 6,89 36,0 12 9 9 9 81 81 7,53 81,0 13 10 10 10 100 100 8,16 100,0 14  55 53 344 385 345 Рис. 2-2		BX + NA = Y
		BX2+AX =XY

Решив эту систему, получим:

B=	NXY – XY		A=	YX
	NX2 – XX			

Оценить функциональную близость (в линейном смысле) значений Х и Y можно с помощью коэффициента корреляции R, который находится по следующей формуле

R=	NXY – XY
	(NX2 – XX) (NY2 – YY)

Принято считать, что при R0,3 наблюдается слабая линейная связь, при R=0,30,7 – средняя, при R0,7 – сильная, при R0,9 – весьма сильная связь, при R=1 – полная функциональная связь (все точки Y(X) лежат на одной прямой). Таким образом, R помогает оценить “надежность” наших предположений.

Необходимые вычисления выполним, пользуясь таблицей на рис. 2-2. Здесь клетки, заполненные числами с жирным шрифтом предполагают ввод формул. Клеточные функции E2, D2, G2 получены из соответствующих формул для значений B, A, R (см. выше). В этих формулах знак означает сумму соответствующих величин (у нас 14-я строка), знак N – количество опытов (у нас 10), вычисляется функцией СЧЁТ).

D4=B4*C4, E4=B4^2, G4=C4^2, F4=E$2+D$2*B4,

E2=(СЧЁТ(B4:B13)*D14-B14*C14)/(СЧЁТ(B4:B13)*E14-B14*B14), D2=(C14-E2*B14)/СЧЁТ(B4:B13),

G2=(СЧЁТ(B4:B13)*D14-B14*C14)/(КОРЕНЬ(СЧЁТ(B4:B13)*E14-B14*B14)*

КОРЕНЬ(СЧЁТ(B4:B13)*G14-C14*C14)).

Для анализа результатов найдем значение функции Y(X) для всех заданных аргументов (столбец F). Видим, что расхождение между фактическими и полученными значениями достаточно заметно. Для вычисления коэффициента корреляции R нам понадобилось еще значение суммы квадратов функции (столбец G). В нашем случае R=0,722.

Содержимое клетки Е2 представлено в пользовательском формате вида +#,00"x";–0,00"х" с тем, чтобы отображался и знак плюс и буква Х. В строке 14 все формулы являются суммами вышележащих ячеек в диапазоне с 4 по 13 строки.

Полученное уравнение регрессии таково: Y=1,8+0,64X.

Таким образом, если нам понадобится вычислить ожидаемое значение прибыли Y в будущем, например, при капиталовложениях в сумме 20 единиц, нужно подставить их в найденную функцию Y=1,8+0,64*20=14,6. Однако достоверность такого предположения может оказаться не достаточно высокой, ввиду того, что линейное описание процесса, возможно, слишком примитивно. Техника аппроксимации более сложными функциями будет изучена ниже.

Сначала рассмотрим встроенные функции Excel (ЛИНЕЙН() и ТЕНДЕНЦИЯ()) для более быстрого нахождения коэффициентов уравнения линейной регрессии.

ЛИНЕЙН(<известное Y>;<известное X>) – вычисляет два коэффициента линейного уравнения регрессии для множества значений независимой переменной Х и зависимой – Y. Результат выводится в две смежные ячейки – сначала коэффициент при Х, затем – свободный член. Ввиду этого функция должна вводиться как функция обработки массива. Сначала в В4 вводим функцию (без фигурных скобок) и нажимаем Enter, далее выделяем одновременно ячейки В4 и С4 и переходим в режим редактирования клавишей F2. Потом нажимаем клавиши Ctrl+Shift+Enter (вместо обычного Enter).

Пример. Если исходные данные расположены как показано на рис. 2-3, и в В3:C3 введена функция

{=ЛИНЕЙН(B2:K2;B1:K1)},

результаты в клетках В4 и С4 можно интерпретировать как коэффициенты линейного уравнения регрессии y=0,6364x+1,8.

ТЕНДЕНЦИЯ(<известное Y>;<известное X>;<новое X>) – вычисляет ожидаемое новое значение Y для нового Х, если известны некоторые опытные значения X и Y. Вычисления делаются в предположении, что Х и Y зависят линейно.

Пример: Исходные данные расположены (рис. 2-3) в клетке G3, результат – в Н3. Видим, что в предположении линейного тренда при Х=12 ожидаемое Y=9,44.

H4=ТЕНДЕНЦИЯ(B$2:K$2;B$1:K$1;G4).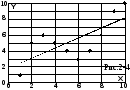

	A	B	C	D	E	F	G	H	I	J	K
1	X	1	2	3	4	5	6	7	8	9	10
2	Y	1	5	6	5	4	3	4	6	9	10
3		0,636	1,8				12	9,44		Рис.	2-3

Таким образом, при Х=12 ожидается Y=9,44.

Используя значения X и Y с помощью Excel, построим график, совмещенный с линией регрессии (линией тренда), как показано на рис. 2-4.

В Excel имеется очень простой способ строить линейную аппроксимацию равноотстоящих значений аргумента. Для этого нужно выделить известные значения прогнозируемой величины и потянуть за маркер заполнения, удерживая правую кнопку мыши. Затем, из появившегося контекстного меню (его фрагмент приведен на рис. 2-5) выбрать пункт Линейное приближение. В заполняемых клетках мы обнаружим значения, вычисленные системой для найденного ею линейного уравнения регрессии.

На рис.2-6 исходными данными являются 2,4,5. Остальные числа являются вычисленным прогнозом в предположении линейной связи аргументов в соответствии с найденным Excel уравнением.

2

4

5

6,67

8,17

9,67

11,17

12,67

Рис. 2-6

Здесь же (рис. 2-7) доступно и Экспоненциальное приближение.

2

4

5

8,55

13,52

21,37

33,80

53,44

Рис. 2-7

Графическое отображение обеих кривых представлено на рис. 2-8.

С помощью средств деловой графики можно не только построить необходимые кривые, но получить линии тренда и соответствующие им уравнения Y(X). Здесь y=1,5x+0,6667 для линейного закона (обозначены кружками), y=1,368e^0,4581x – для экспоненты (точки). Исходные точки обведены овалом.

3. Нелинейная регрессия. Видим (рис. 2-4), что, хотя уравнение регрессии правильно отражает направление роста функции, оно является достаточно грубым приближением. Здесь необходимо воспользоваться более сложной аппроксимирующей функцией. В качестве таких функций часто используют степенные полиномы разной степени вида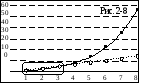

Y = a+bX+cX²+dX³+eX⁴+ ...

Для розыска коэффициентов такого уравнения воспользуемся средством Поиск решения (вкладка Данные, группа Анализ).

Пусть нам заданы уже известные значения Х и Y. В таблице на рис. 3-1 эти данные отображены в столбцах Аргумент Х и Функция Y. В колонках Прямая, Парабола и 3-я степень будут отображены квадраты погрешностей между фактическим значением Y и полученным из уравнений регрессии первой, второй и третьей степени соответственно.

	A	B	C	D	E
1	Подбор коэффициентов регрессии
2	Коэф. Y(х)	a	b	c	d
3	a+bx	1,800	0,636
4	a+bx+cx2	4,050	–0,489	0,102
5	a+bx+cx2+dx3	–2,033	4,907	–1,067	0,071
6			П о г р е	ш н о с	т и
7	Аргумент X	Функция Y(Х)	Прямая	Пара- бола	3-я степень
8	1	1,00	2,063	7,095	0,769
9	2	5,00	3,714	2,305	0,851
10	3	6,00	5,248	6,227	1,013
11	4	5,00	0,428	1,608	0,003
12	5	4,00	0,964	0,027	0,455
13	6	3,00	6,855	3,240	1,663
14	7	4,00	5,083	2,693	0,104
15	8	6,00	0,794	0,471	0,644
16	9	9,00	2,169	1,131	2,753
17	10	10,00	3,372	0,371	1,387
18	Сумма квадратов:		30,691	25,168	9,641
					Рис.3-1

В общем случае это выражение вида