- •Оглавление
- •Введение
- •Глава 1. Электростатическое поле в вакууме
- •. Закон сохранения электрического заряда
- •1.2. Закон Кулона
- •1.3. Напряженность электрического поля
- •1.4. Потенциал электрического поля
- •1.5. Поле электрического диполя в вакууме
- •1.6. Теорема Гаусса–Остроградского для электростатического поля в вакууме
- •1.6.1. Электростатическое поле заряженной сферы
- •1.6.2. Электростатическое поле заряженного шара
- •1.6.3. Электростатическое поле заряженной бесконечной плоскости
- •1.6.4. Электростатическое поле заряженного бесконечно длинного цилиндра
- •Глава 2. Электростатическое поле в диэлектриках
- •2.1. Дипольные моменты молекул диэлектрика
- •2.1.1. Неполярный диэлектрик во внешнем электростатическом поле
- •2.1.2. Полярный диэлектрик во внешнем электростатическом поле
- •2.2. Поляризация диэлектриков
- •2.3. Теорема Гаусса–Остроградского для электростатического поля в изотропной диэлектрической среде
- •2.4. Закон Кулона для электростатического поля в изотропной диэлектрической среде
- •2.5. Условие для электростатического поля на границе раздела двух изотропных диэлектрических сред
- •2.6. Сегнетоэлектрики
- •Глава 3. Проводники в электростатическом поле
- •3.1. Распределение зарядов в проводнике
- •3.2. Электрическая емкость уединенного проводника
- •3.3. Взаимная электрическая емкость двух проводников. Конденсаторы
- •3.4. Энергия заряженных проводников и электростатического поля
- •Глава 4. Электрический ток в металлах, растворах электролитов и газах
- •4.1. Классическая теория электропроводности металлов
- •4.2. Законы постоянного тока в проводниках
- •4.2.1. Закон Ома для полной цепи
- •4.2.2. Правила Кирхгофа
- •4.3. Постоянный ток в жидкостях (растворах электролитов)
- •4.4. Постоянный ток в газах
- •Глава 5. Электрический ток в вакууме
- •5.1. Работа выхода электрона из металла
- •5.2. Электронно-вакуумный диод
- •5.3. Электронно-вакуумный триод
- •Глава 6. Переходные процессы в rc-цепях
- •6.1. Заряд и разряд конденсатора
- •6.2. Конденсатор в цепи гармонического переменного тока
- •Приложение некоторые сведения из разделов математики
- •Комплексная арифметика
Приложение некоторые сведения из разделов математики
Выбор системы координат и некоторые действия над векторами
Для математического нахождения положения точки в пространстве строится прямоугольная система координат, введенная Р.Декартом. Все три оси в декартовый системе координат взаимно перпендикулярны. Оси координат обозначают: x, y, z. Возможны два варианта ориентации осей координат –правовинтовая и левовинтовая. Правовинтовая декартова система координат построена так, что ось z имеет положительные направления в направлении закручивания правого винта от оси x к оси y по минимальному (прямому) углу. В зависимости от выбора направлений осей, некоторые операции над векторами, в частности векторное произведение, меняются по знаку на противоположный. Все дальнейшие определения приводятся к правовинтовой системе координат.
Единичные
отрезки, отсекаемые на осях координат
называются ортами осей координат и
обозначаются i,
j
и k.
Орты осей координат являются единичными
векторами, направленными по направлению
оси. Радиус-вектор
,
проведенный из начала координат,
определяется его проекциями на
координатные оси x,y
и z,
следующим образом:
![]() .
.
Вектором,
называется направленный отрезок прямой.
Скаляром называется любая не векторная
величина, имеющая только значение.
Координаты вектора
![]() ,
через его конец
,
через его конец
![]() и
начало
и
начало
![]() ,
определяются:
,
определяются:
![]() .
Модуль или длина вектора
.
Модуль или длина вектора
![]() ,
равна
,
равна
![]() .
.
Над
векторами разрешены операции сложения
и умножения. Пусть заданы векторы
![]() и
и
![]() ,
тогда:
,
тогда:
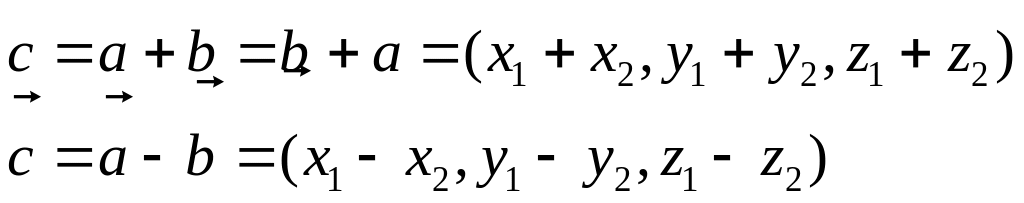 .
.
Операций
умножения две: скалярная, обозначаемая
![]() или
или
![]() ,
и векторная –
,
и векторная – ![]() или
или
![]() :
:
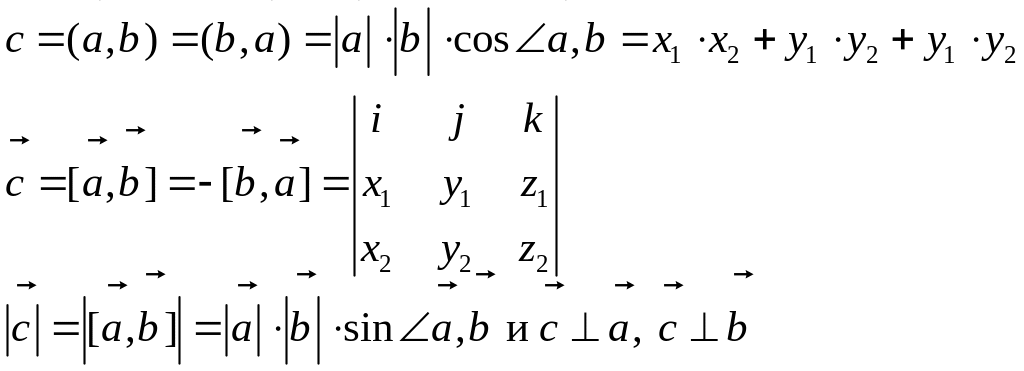 .
.
Направление
вектора
![]() выбирается в сторону, куда по минимальному
углу от вектора
к вектору
выбирается в сторону, куда по минимальному
углу от вектора
к вектору
![]() закручивается
правый винт.
закручивается
правый винт.
Смешанное
векторное произведение
![]() .
.
Пусть в
пространстве задано векторное поле
![]() ,
то можно вычислить градиент, дивергенцию
и ротор векторного поля. Вектор градиента
показывает направление возрастания
функции
,
т.е. направление кратчайшего хода к
вершине горы функции. Дивергенция
вектора, показывает скорость нарастания
функции, т.е. как долго мы пойдем к вершине
с постоянной скоростью. Ротор вектора,
показывает, направление возможных
отклонений на пути к вершине.
,
то можно вычислить градиент, дивергенцию
и ротор векторного поля. Вектор градиента
показывает направление возрастания
функции
,
т.е. направление кратчайшего хода к
вершине горы функции. Дивергенция
вектора, показывает скорость нарастания
функции, т.е. как долго мы пойдем к вершине
с постоянной скоростью. Ротор вектора,
показывает, направление возможных
отклонений на пути к вершине.
Градиент вектора:
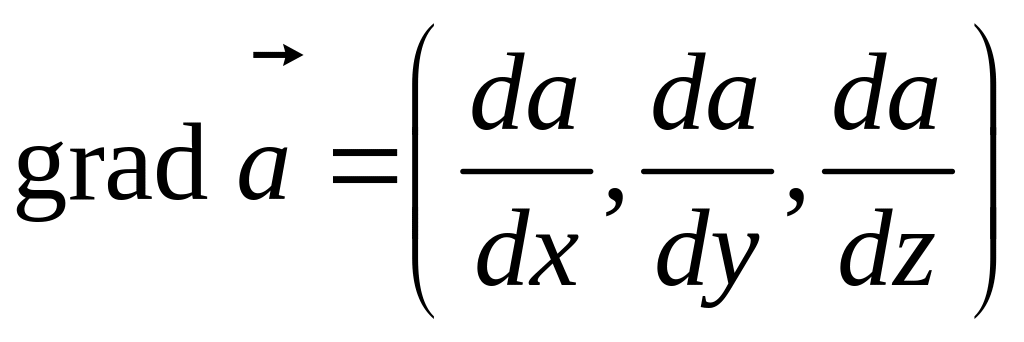
Дивергенция вектора:

где V – объем, ограниченный замкнутой поверхностью, площадью S
Ротор вектора:
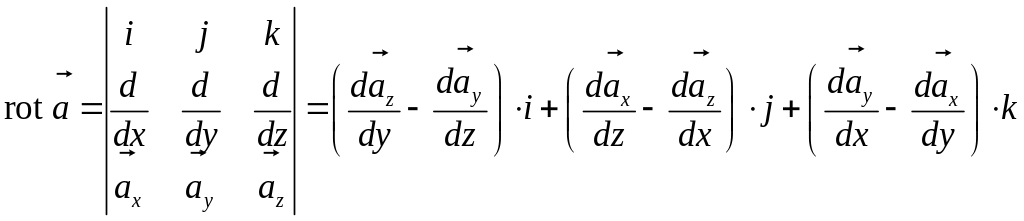
Оператор
Гамильтона или набла-оператор:
 .
.
Тогда:
![]() (действие
оператора на вектор);
(действие
оператора на вектор);
![]() (скалярное
произведение);
(скалярное
произведение);
![]() (векторное
произведение).
(векторное
произведение).
Правила дифференцирования и интегрирования
Если
![]() ,
,
![]() и
и
![]() ,
то справедливы следующие выражения
дифференцирования:
,
то справедливы следующие выражения
дифференцирования:
![]()
![]()
![]()
![]()
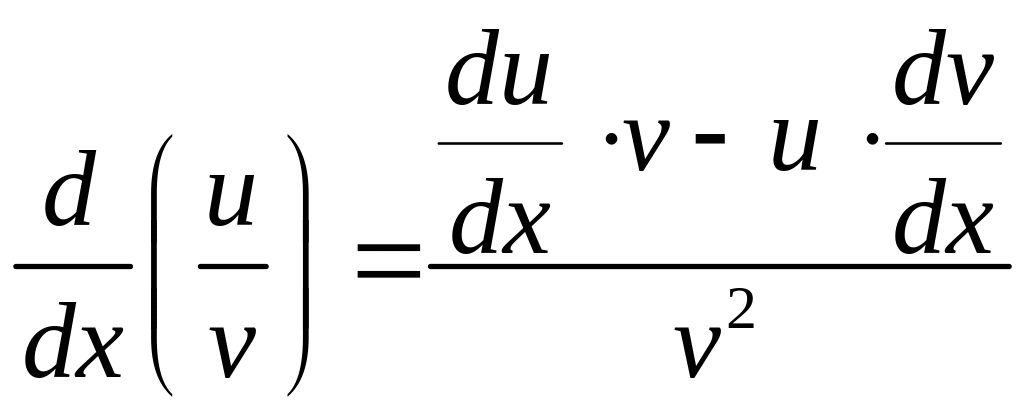 .
.
Дифференцирование векторного произведения производится по правилу:
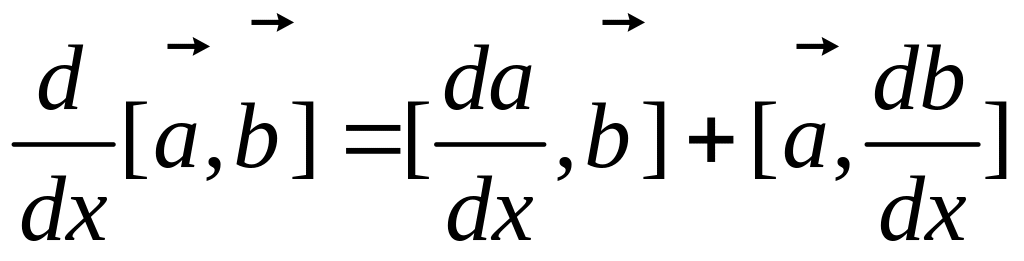 .
.
Если , и , то справедливы следующие выражения интегрирования:
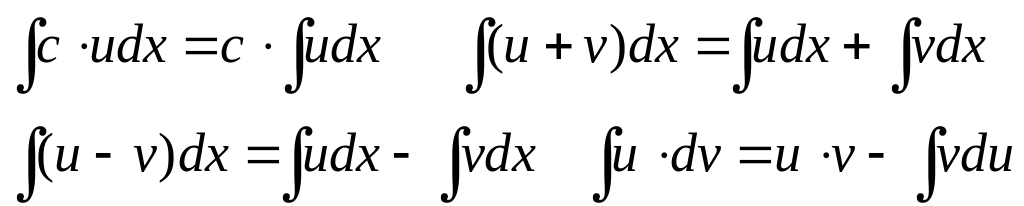 .
.
Комплексная арифметика
Мнимой,
или комплексной единицей называют число
![]() ,
получаемое при решении уравнения
,
получаемое при решении уравнения
![]() .
.
С введением комплексного числа, можно любое число z на множестве всех чисел представить в виде:
![]() ,
,
где Re – действительная часть числа, а Im – мнимая.
Число
![]() называют
комплексно сопряженным числу z.
называют
комплексно сопряженным числу z.
Квадратом модуля комплексного числа, по аналогии с квадратом модуля вектора, называют величину:
![]() .
.
Из определения квадрата модуля комплексного числа, легко доказать формулу Эрланга:
![]() ,
,
где x – любое действительное число, а z – комплексное.
Докажем это, вычисляя квадрат модуля комплексного числа:
![]()
Применяя определения комплексного числа и формулу Эрланга можно доказать:
![]() ,
где
,
где
![]() – константы,
или:
– константы,
или:
![]()
![]() и
и