- •Содержание
- •1. Геометрическая оптика Краткая теория
- •Обратимости светового луча;
- •Постулат Ферма, называемый принципом наименьшего времени:
- •2. Дисперсия и поляризация света Краткая теория
- •Интенсивность света, прошедшего через оба поляроида, будет
- •Задачи для самостоятельного решения
- •3. Интерференция и дифракция света Краткая теория
- •Интерференция в тонких пленках
- •Изображение колец Ньютона
- •4. Элементы квантовой оптики Краткая теория
- •Для серого тела
- •При этом условии средняя энергия осциллятора оказалась равной
- •Формула для массы фотона
- •5. Элементы квантовой физики. Принцип неопределенности гейзенберга. Краткая теория
- •Задачи для самостоятельного решения
- •6. Квантовые состояния. Уравнения шредингера. Краткая теория
- •Вопросы для самоподготовки
- •Задачи для самостоятельного решения
- •7. Атом водорода. Сериальные закономерности. Краткая теория
- •Задачи для самостоятельного решения
- •8. Элементы ядерной физики Краткая теория
- •Размер ядра характеризуется радиусом ядра, имеющим условный смысл ввиду размытости границ ядра.
- •Вопросы для самоподготовки
- •Задачи для самостоятельного решения
- •Приложения
- •Список использованной литературы
Задачи для самостоятельного решения
6.1.
Волновая функция, описывающая некоторую
частицу, имеет вид
![]() ,
где r
– расстояние этой частицы до силового
центра; а – некоторая постоянная;
,
где r
– расстояние этой частицы до силового
центра; а – некоторая постоянная;
![]() - нормировочный коэффициент волновой
функции. Определите среднее расстояние
частицы до силового центра.
- нормировочный коэффициент волновой
функции. Определите среднее расстояние
частицы до силового центра.
(Ответ:
![]() ).
).
6.2.
Волновая функция, описывающая состояние
электрона в одномерной прямоугольной
потенциальной яме с бесконечно высокими
стенками, имеет вид
![]() ,
l
– ширина ямы. Определите среднее значение
,
l
– ширина ямы. Определите среднее значение
![]() координаты электрона.
координаты электрона.
(Ответ:
![]() ).
).
6.3.
Радиальная часть волновой функции для
электрона в состоянии 3d
имеет вид
![]() ,
где
,
где
![]() м – первый боровский радиус. Вычислить
расстояние, на котором радиальная
составляющая вероятности местонахождения
имеет максимум в этом случае.
м – первый боровский радиус. Вычислить
расстояние, на котором радиальная
составляющая вероятности местонахождения
имеет максимум в этом случае.
(Ответ:
![]() м)
м)
6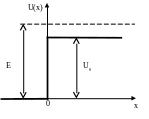 .4.
Частица с массой m
и энергией E
движутся в потенциальном поле U(x),
показанном на рисунке, в положительном
направлении оси ОХ.
Найти коэффициент отражения R
этого потенциального барьера для случая
E>U0
.4.
Частица с массой m
и энергией E
движутся в потенциальном поле U(x),
показанном на рисунке, в положительном
направлении оси ОХ.
Найти коэффициент отражения R
этого потенциального барьера для случая
E>U0
(Ответ:
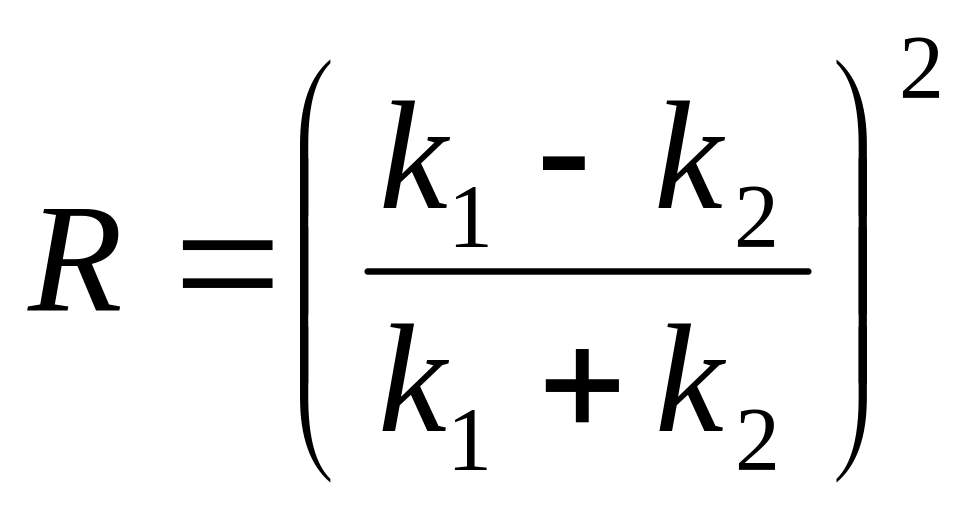 )
)
6.5. Электрон находится в бесконечно глубоком одномерном, прямоугольном потенциальном ящике, шириной l. В каких точках в интервале (0 < x < l) плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить плотность вероятности для этих точек. Решение пояснить графиком.
(Ответ:
![]() )
)
6.6.
В прямоугольной потенциальной яме
шириной l
с абсолютно непроницаемыми стенками
(0 < x
< l)
находится частица в основном состоянии.
Вычислить вероятность нахождения
частицы в области
![]() .
.
(Ответ:
![]() )
)
6.7. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности?
(Ответ:
![]() )
)
6.8.
Частица находится в бесконечно глубоком,
одномерном, прямоугольном потенциальном
ящике. Найти отношение разности
![]() соседних энергетических уровней к
энергии En
частицы в
следующих случаях: 1) n=2;
2) n=5;
3)
соседних энергетических уровней к
энергии En
частицы в
следующих случаях: 1) n=2;
2) n=5;
3)
![]() .
.
(Ответ:
![]() )
)
6.9.
Волновая функция, описывающая движение
электрона в основном состоянии атома
водорода, имеет вид
![]() ,
где А –
нормировочный коэффициент;
,
где А –
нормировочный коэффициент;
![]() м – первый боровский радиус. Найти для
основного состояния атома водорода
среднее значение кулоновской силы.
м – первый боровский радиус. Найти для
основного состояния атома водорода
среднее значение кулоновской силы.
(Ответ:
![]() Н )
Н )
6.10. Протон с энергией 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой 10 эВ и шириной 0,1 нм. Определите вероятность прохождения протоном этого барьера. Во сколько раз надо сузить барьер, чтобы вероятность прохождения его протоном была такой же, как для электрона при вышеприведенных условиях.
(Ответ:
![]() ).
).
7. Атом водорода. Сериальные закономерности. Краткая теория
Исследования спектров излучения разреженных газов (т.е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водорода.
Электрон может переходить скачком с одной орбиты на другую. Переход с более удаленной орбиты на более близкую связан с испусканием одного фотона, - такова причина возникновения характерного для одноатомного вещества, в данном случае водорода, линейчатого спектра.
Швейцарский ученый И. Бальмер (1825—1898) подобрал эмпирическую формулу, описывающую спектральные линии излучения атома водорода в видимой области спектра:
|
(7.1) |
где R=3,29 1015 c -1 - постоянная Ридберга, n - номер орбиты, на которую перешел электрон, 2 - номер орбиты, с которой он перешел при испускании данного фотона.
Из формулы (7.1) вытекает, что спектральные линии, отличающиеся различными значениями n, образуют группу или серию линий, называемую серией Бальмера. С увеличением n линии серии сближаются; значение n= определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.
В дальнейшем в спектре атома водорода было обнаружено еще несколько серий. В ультрафиолетовой области спектра находится серия Лаймана:
|
(7.2) |
В инфракрасной области спектра были также обнаружены:
серия Пашена
|
(7.3) |
серия Брэкета
|
(7.4) |
серия Пфунда
|
(7.5) |
серия Хэмфри
|
(7.6) |
Анализируя уравнения (7.1) – (7.6) можно записать общее уравнение, описывающее все сериальные закономерности излучения атома водорода
|
(7.7) |
где m- номер орбиты, на которую перешел электрон при испускании фотона, m < n, m = 1, 2, 3, 4, 5, 6.
Согласно классическим представлениям атом мог бы испускать монохроматическую волну (т.е. спектральную линию) в том случае, когда электрон в излучающем атоме совершает гармонические колебания и, следовательно, удерживается около положения равновесия квазиупругой силой. Первая попытка создания на основе накопленных сведений «модели» атома, т.е. представления о его структуре принадлежит Д.Д. Томсону (1903 г.). Томсон полагал, что атом представляет собой сферу, заполненную положительно заряженной материей, в которой движутся корпускулы – электроны. Но эта модель не смогла объяснить таблицы Менделеева – периодичности свойств атомов. В 1909 г. на основании результатов экспериментов по рассеянию α – частиц тонкими металлическими фольгами и следствий, к которым привели эти эксперименты, Резерфордом была предложена ядерная (планетарная) модель атома. Согласно этой модели, атом представляет собой систему зарядов, в центре которой расположено тяжелое положительное ядро с зарядом Ze, имеющее размеры, не превышающие 10-14 м, а вокруг ядра расположены Z электронов, распределенных по всему объему, занимаемому атомом. Почти вся масса атома сосредоточена в ядре. Исходя из таких предположений, Резерфорд разработал количественную теорию рассеяния α – частиц. По представлениям Резерфорда атом подобен солнечной системе («Солнце» - ядро, «планеты» - электроны).
Первая попытка разобраться в особенностях, свойственных атомам была сделана известным датским физиком Н. Бором. Бор сделал вывод, что энергия атомов не может меняться непрерывно. Возможные состояния атома образуют дискретную последовательность, и энергия атома в этих состояниях образует дискретный ряд. Изменение состояния (и энергии) атома может происходить лишь в виде скачка - от одного возможного состояния к другому.
Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.
В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию
|
(7.8) |
где me — масса электрона, — его скорость по n-й орбите радиуса rn. Целое число n равно числу длин волн де Бройля для электронов, укладывающихся на длине круговой орбиты.
Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией равной разности энергий соответствующих стационарных состояний
|
(7.9) |
где
![]() ,
и Wm
— соответственно
энергии стационарных состояний атома
до и после излучения (поглощения), где
R – постоянная Ридберга, n – главное
квантовое число,.
,
и Wm
— соответственно
энергии стационарных состояний атома
до и после излучения (поглощения), где
R – постоянная Ридберга, n – главное
квантовое число,.
При Еm<Еn происходит излучение фотона (переход атома из состояния с большей энергией в состояние с меньшей энергией, т. е. переход электрона с более удаленной от ядра орбиты на более близлежащую), при Еm>Еn — его поглощение (переход атома в состояние с большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретных частот квантовых переходов и определяет линейчатый спектр атома.
Согласно Бору, радиус n-й стационарной орбиты:
|
(7.10) |
где n= 1, 2, 3, ....
Для атома водорода (Z = 1) радиус первой орбиты электрона при n = 1, называемый первым боровским радиусом (а), равен
|
(7.11) |
Полная
энергия электрона в водородоподобной
системе складывается из его кинетической
энергии (![]() )
и потенциальной энергии в электростатическом
поле ядра (
)
и потенциальной энергии в электростатическом
поле ядра (![]() ):
):
|
(7.12) |
Учитывая квантованные для радиуса n-й стационарной орбиты значения получим, что энергия электрона может принимать только следующие дискретные значения:
|
(7.13) |
где знак минус означает, что электрон находится в связанном состоянии. Целое число п в выражении (7.13), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n = 1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.
С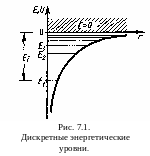 остояние
электрона в атоме водорода описывается
волновой функцией ,
удовлетворяющей стационарному уравнение
Шредингера.
остояние
электрона в атоме водорода описывается
волновой функцией ,
удовлетворяющей стационарному уравнение
Шредингера.
Решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения Е1, Е2, Е3…, показаны на рис. 7.1 в виде горизонтальных прямых. Самый нижний уровень Е1, отвечающий минимальной возможной энергии, — основной, все остальные (Еn > Е1, n = 2, 3, ...) — возбужденные. Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n = E = 0. При Е > 0 движение электрона является свободным; область непрерывного спектра Е > 0 (заштрихована на рис. 7.1) соответствует ионизованному атому.
Собственные значения оператора квадрата момента импульса равнs
|
(7.14) |
где l-квантовое число, называемое азимутальным.
Модуль момента импульса может иметь лишь дискретные значения, определяемые формулой
|
(7.15) |
Оператор проекции момента импульса на ось OZ
|
(7.16) |
где m – магнитное квантовое число. Таким образом, магнитное квантовое число m определяет проекцию момента импульса электрона на заданное направление.
Момент импульса системы, состоящей из нескольких микрочастиц, равен сумме моментов отдельных частиц. Суммарный момент, как и всякий момент, определяется
, |
(7.17) |
где l – азимутальное квантовое число результирующего момента.
Расщепление спектральных линий называется тонкой структурой. Для объяснения тонкой структуры спектральных линий, американские физики Д. Уленбек и С. Гаудсмит предположили, что у электрона помимо момента импульса L и соответствующей ему проекции момента импульса на ось OZ Lz имеется собственный механический момент импульса Ls , называемый спином электрона. Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.
Если электрону приписывается собственный механический момент импульса (спин) Ls то ему соответствует собственный магнитный момент Lsz. Согласно общим выводам квантовой механики, спин квантуется по закону:
|
(7.18) |
где s-спиновое квантовое число.
По аналогии с орбитальным моментом импульса, проекция Lsz спина квантуется так, что вектор Ls может принимать 2s+1 ориентации. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением:
|
(7.19) |
где ms — магнитное спиновое квантовое число; оно может иметь только два значения: тs=±1/2.
Таким образом, экспериментальные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ
7.1. Серия Бальмера для видимой области спектра.
7.2. Серия Лаймана для ультрафиолетовой области спектра атома водорода.
7.3. Серия Пашена для инфракрасной области спектра атома водорода.
7.4. Серия Брэкета для спектра атома водорода.
7.5. Серия Пфунда для спектра атома водорода.
7.6. Серия Хэмфри для спектра атома водорода.
7.7. Обобщенная формула, описывающая сериальные закономерности излучения атома водорода.
7.8. Граница серии.
7.9. Первый постулат Бора.
7.10. Дискретные квантованные значения момента импульса.
7.11. Второй постулат Бора.
7.12. Радиус n-й стационарной орбиты.
7.13. Первый боровский радиус.
7.14. Полная энергия электрона в водородоподобной системе.
7.15. Главное квантовое число.
7.16. Основное и возбужденное состояние.
7.17. Связь энергии атома со спектральным термом.
7.18. Собственные значения квадрата момента импульса.
7.19. Модуль момента импульса.
7.20. Проекция момента импульса на ось OZ.
7.21. Момент импульса системы.
7.22. Механический момент импульса (спин).
7.23. Проекция спина на направление внешнего магнитного поля.
7.24. Магнитное спиновое квантовое число.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «АТОМ ВОДОРОДА. СЕРИАЛЬНЫЕ ЗАКОНОМЕРНОСТИ»
Записать обобщенную формулу, описывающую сериальные закономерности излучения атома водорода.
Записать дополнительные уравнение, позволяющие определить неизвестные величины.
Решить полученную систему уравнений.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «АТОМ ВОДОРОДА. СЕРИАЛЬНЫЕ ЗАКОНОМЕРНОСТИ»
Задача 7.1. Определите изменение орбитального механического момента электрона при переходе его из возбужденного состояния в основное с испусканием фотона с длиной волны λ = 1,02·10-7 м.
Дано: λ = 1,02·10-7 м m = 1 R = 1,1·10-7 м-1 |
Решение: 1. Согласно обобщенной формуле (7.7)
|
||
Δ L-? |
Учитывая, что частота и длина волны связаны следующим соотношением |
|
|
получим, что
|
(2) |
Из уравнения (2) находим
|
(3) |
Согласно уравнению (7.8) дискретные квантованные значения момента импульса, удовлетворяют условию
|
(4) |
Следовательно, разность изменения орбитального момента электрона
|
(5) |
Подставляя уравнение (3) в формулу (5) получим:
|
|
Вычисления:
|
|
Ответ:
![]() Дж с.
Дж с.
Дано: Z=1 n=3 |
Решение:
Второй закон Ньютона для электрона, движущегося по окружности под действием кулоновской силы, имеет вид |
v -? |
|
Задача 7.2. Определите скорость v электрона на третьей орбите водорода (Z=1, n=3).
|
(1) |
Из уравнения (1) найдем радиус орбиты
|
(2) |
Согласно формуле (7.8) дискретные квантованные значения момента импульса, удовлетворяют условию
|
(3) |
Подставляя уравнение (2) в формулу (3) получим
|
(4) |
Учитывая,
что
![]() ,
получим
,
получим
|
|
Вычисления:
|
|
Ответ:
![]() м/с.
м/с.

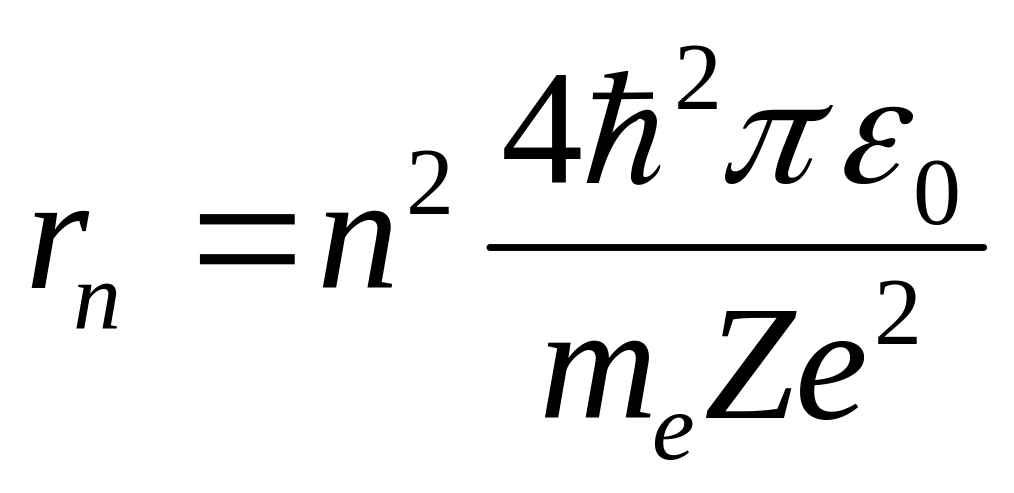 ,
,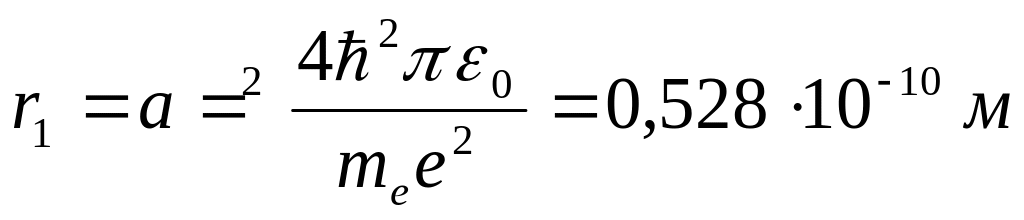
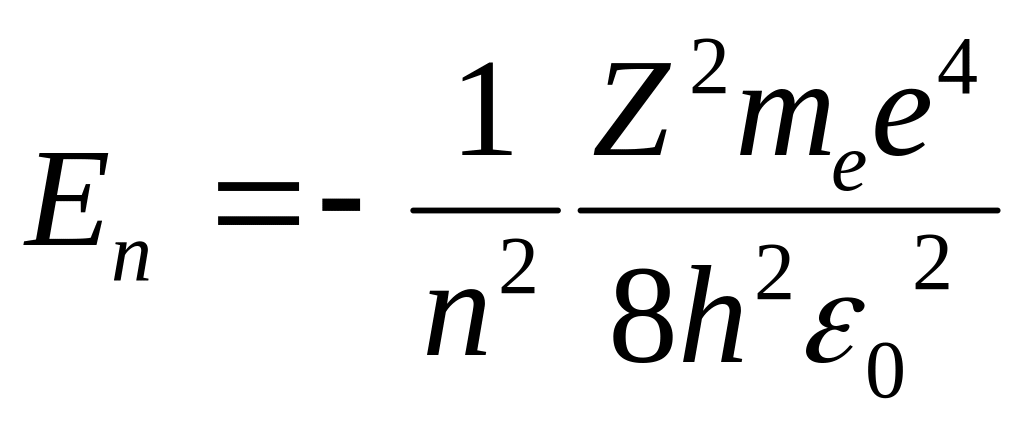 (n=1, 2, 3, 4,...),
(n=1, 2, 3, 4,...),
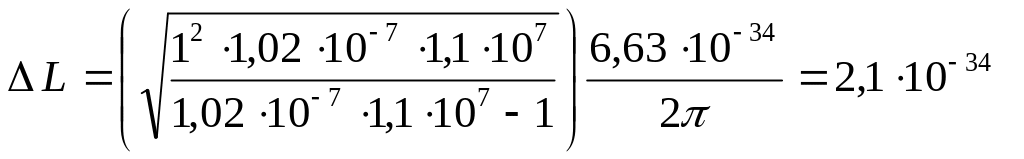 Дж
с
Дж
с