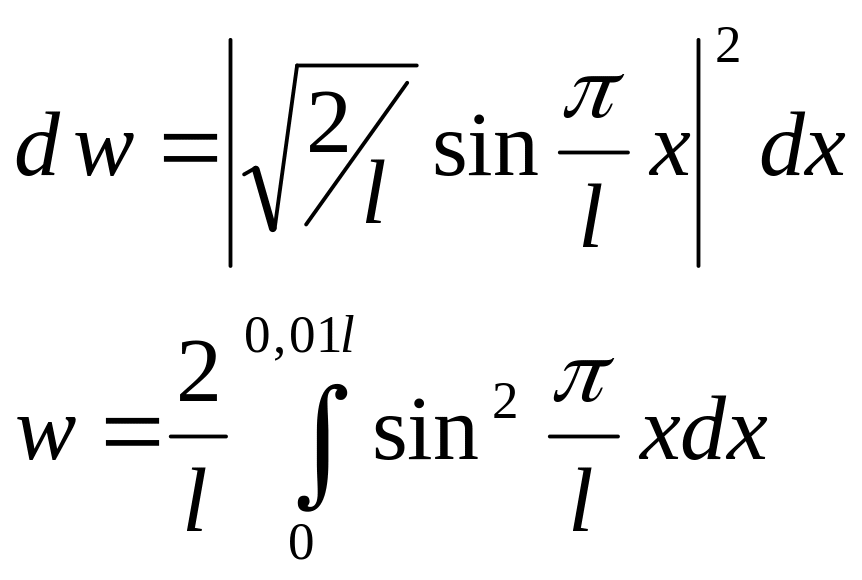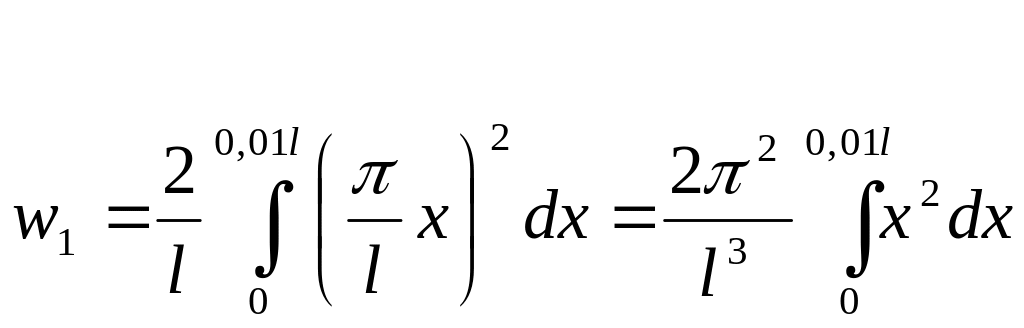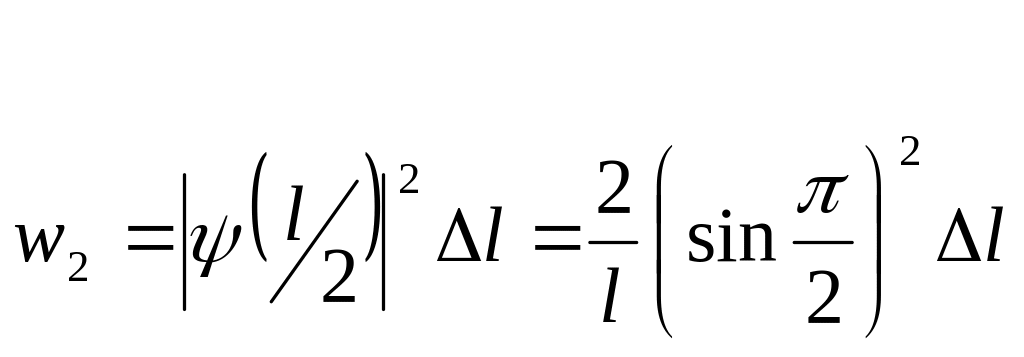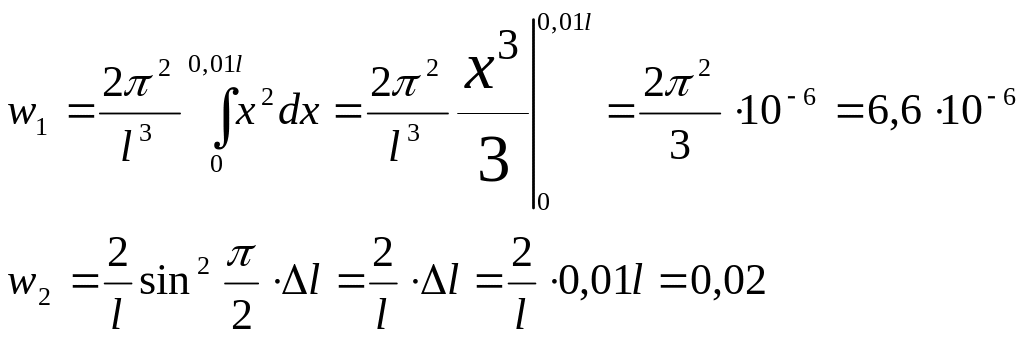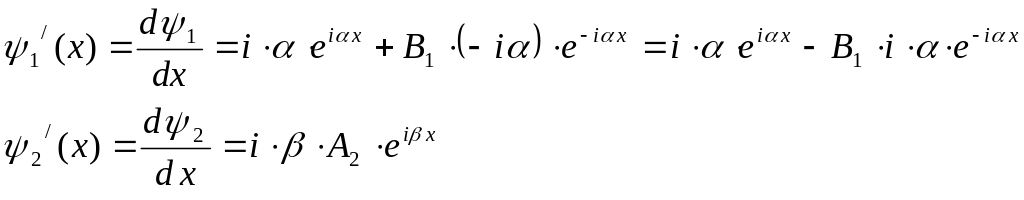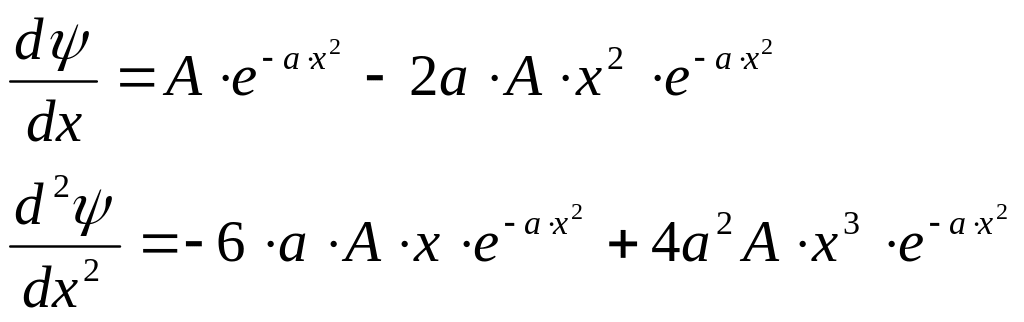Вопросы для самоподготовки

6.1. Определение волновой функции.

6.2. Определение плотности вероятности.

6.3. Условие нормировки вероятностей.

6.4. Общее уравнение Шредингера.

6.5. Стационарное уравнение Шредингера.

6.6. Условия регулярности  - функции.

6.7. Оператор Лапласа.

6.8. Собственная функция.

6.9. Собственные значения энергии.

6.10. Спектр величины

6.11. Дискретный спектр величины.

6.12. Непрерывный спектр величины.

6.13. Уравнение Шредингера для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме.

6.14. Собственные функции частицы, находящейся в бесконечно глубокой одномерной потенциальной яме.

6.15. Собственные значения энергии частицы, находящейся в бесконечно глубокой одномерной потенциальной яме.

6.16. Разность энергий для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме.

6.17. Определение оператора.

6.18. Собственные значения оператора квадрата момента импульса.

6.19. Суммарный момент импульса.

6.20. Принцип суперпозиции состояний.

6.21. Коэффициент прозрачности потенциального барьера.

6.22. Коэффициент отражения потенциального барьера.

6.23. Эффективная глубина.

6.24. Определение линейного осциллятора.

6.25. Уравнение Шредингера для линейного осциллятора.

6.26. Правило отбора.

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ:

«КВАНТОВЫЕ СОСТОЯНИЯ. УРАВНЕНИЕ ШРЕДИНГЕРА»

1. Записать уравнение Шредингера в стационарном состоянии (или уравнение волновой функции).

2. Записать дополнительные уравнения, необходимые для нахождения неизвестной величины.

3. Решить полученную систему уравнений относительно неизвестной величины.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ:

«КВАНТОВЫЕ СОСТОЯНИЯ. УРАВНЕНИЕ ШРЕДИНГЕРА»

Задача 6.1. Волновая функция описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность нахождения частицы в малом интервале Δl=0,01l в двух случаях: 1) вблизи стенки ; 2) в средней части ящика .

Дано: Δl=0,01l 1) ; 2)	Решение: Запишем уравнение волновой функции (1) Согласно уравнению (6.3), вероятность того, что частица будет обнаружена в интервале dx (от x до x+dx), (2)
	3. Подставляя уравнение (1) в (2) получим, что вероятность нахождения частицы вблизи стенок ящика
		(3)

Так как x изменяется в интервале и, следовательно, , справедливо приближенное равенство , т.е.

.

(4)

С учетом (4) уравнение (3) примет вид:

Так как квадрат модуля волновой функции вблизи ее максимума в заданном малом интервале (Δl=0,01l) практически не изменяется, во втором случае интегрированием можно пренебречь. Поэтому искомая вероятность во втором случае определяется выражением

Вычисления:

О твет: w₁=6,6·10^-6, w₂=0,02.

Задача 6.2. Частица находится в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками». Найти решение уравнения Шредингера в пределах «ямы» (0 ≤x ≤l).

Дано: 0≤x≤l, U=0 x<0, U→∞ x>l, U→∞	Решение: Запишем уравнение Шредингера в стационарном состоянии, согласно уравнению (6.7): (1)
Ψ(x)-?	По условию задачи 0 ≤x ≤l и U=0, тогда уравнение Шредингера будет иметь следующий вид:

, (2)

т.к. , то уравнение Шредингера примет вид:

(3)

Решая уравнение (3) получим, что

(4)

С учетом начальных условий получаем, что

(5)

Из системы уравнений (5) следует, что

(6)

Тогда уравнение волновой функции будет иметь следующий вид:

.

Ответ: .

З адача 6.3. Частица с энергией E движется в положительном направлении оси ОХ (рис. к задаче) и встречает на своем пути бесконечно широкий прямоугольный барьер высотой U₀, причем E<U₀. Используя условия непрерывности волновой функции и ее первой производной на границе областей 1 и 2 (нормировочный коэффициент А₁=1), определите плотность вероятности обнаружения частицы в точке x=0 области 2.

Дано: E<U0 А1=1	Решение: Согласно уравнению (6.2) плотность вероятности нахождения частицы в данной точке пространства определяется соотношением (1)
(0) - ?

Общее решение Шредингера для частицы, движущейся в потенциальном барьере, согласно уравнению (6.24), имеет вид

,

(2)

где .

Найдем производные волновой функции для областей 1 и 2 с учетом начальных условий

(2)

Учитывая, что получим

(3)

_{Из системы уравнений (3) найдем нормировочный коэффициент А}2

.

(4)

Подставляя уравнение (4) в (1) получим

Ответ: .

Задача 6.4. Определите собственное значение полной энергии гармонического осциллятора, волновая функция которого задана уравнением , где .

Дано:	Решение: Согласно уравнению (6.33) уравнение Шредингера для гармонического осциллятора имеет вид . (1)
Е - ?

Найдем первую и вторую производные данной волновой функции

(2)

Подставляя уравнения (2) в (1) получим

(3)

Из уравнения (3) найдем собственные значение энергии осциллятора

.

Учитывая, что собственная циклическая частота осциллятора , получим

.

Ответ: .