5. Элементы квантовой физики. Принцип неопределенности гейзенберга. Краткая теория

Французский физик Луи де Бройль пришел к выводу, что корпускулярно-волновая двойственность свойств характерна не только для света. Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики – энергия Е и импульс , а с другой стороны – волновые характеристики – частота ν и длина волны λ. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:

,

(5.1)

где h = 6,62 10^-34 Дж · с – постоянная Планка.

Соотношения (5.1) постулировалось не только для фотонов, но и для других микрочастиц (например, электрон, протон, мюзон и т.д. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:

.

(5.2)

Длина волны для частицы с массой m, движущейся со скоростью υ<<c,

.

(5.3)

Если частица имеет кинетическую энергию W, то длина волны

.

(5.4)

Формула де Бройля экспериментально подтвердилась в экспериментах К. Дэвиссона и Л. Джермера, наблюдавших рассеяние электронов монокристаллов никеля.

Соотношением, углубляющим представление о корпускулярно-волновой двойственности свойств частиц, является перенесенная на эти частицы связь между энергией W свободной частицы и частотой ν волн де Бройля:

,

(5.5)

где , ω – циклическая частота. Под свободной частицей понимается частица, движущаяся по инерции в отсутствие внешнего силового поля.

Для совокупности волн, движущихся вместе, следует различать две скорости волн: фазовую υ_фаз и групповую u. Фазовая скорость волн де Бройля для свободного электрона или другой частицы, движущейся со скоростью υ<<c:

,

(5.6)

где - волновой вектор, численное значение которого .

Для частицы, движущейся со скоростью υ>>c, фазовая скорость волны де Бройля будет определяться соотношением

.

(5.7)

Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.

Суперпозиция волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн.

В недиспергирующей среде все плоские волны, образующие пакет, распространяются с одинаковой фазовой скоростью. В этом случае скорость движения пакета совпадает с фазовой скоростью и форма пакета со временем не изменяется. В диспергирующей среде ширина волнового пакета увеличивается. Если дисперсия невелика, увеличение ширины волнового пакета происходит не слишком быстро. В этом случае волновому пакету можно приписать скорость u, под которой понимается скорость, с которой перемещается центр волнового пакета. Эту скорость называют групповой скоростью.

Групповая скорость волн де Бройля:

.

(5.8)

Следовательно, групповая скорость волн де Бройля равна скорости частицы.

Рассмотрим одномерное распространение волны де Бройля вдоль оси OX. Любая волна, в том числе волна де Бройля, независимо от ее природы, характеризуется некоторой волновой функцией Ψ= Ψ (x, t) (пси-функция). Простейшая монохроматическая волна, распространяющаяся вдоль оси OX, описывается волновой функцией

,

(5.9)

где λ – длина волны, – скорость ее распространения.

Р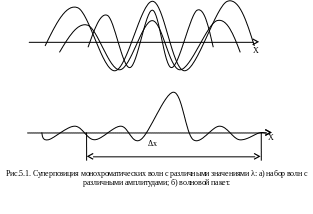 ассмотрим волну, локализованную в некотором интервале . Для того, чтобы волновая функция была отлична от нуля внутри этого интервала и практически равнялась нулю вне его, эта функция должна представлять

суперпозицию монохроматических волн с различными значениями λ.

На рис. (5.1, а) представлен набор таких волн различных амплитуд с динами волн в интервале от λ до , а на рис 5.1,б – результат их

Волновой пакет представляет собой набор монохроматических волн, импульсы которых заключены в интервале

.

(5.10)

Следовательно, увеличение определенности в локализации волны (уменьшение ) связано с одновременным возрастанием в неопределенности импульса Δp. В пределе при Таким образом, электрон, так же как и фотон, не может иметь одновременно определенную координату x и проекцию импульса на ось ОХ p_x. Соотношения между величинами и Δp_x проанализировал В. Гейзенберг. В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел в 1927г. к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом. Обоснование такого соотношения было рассмотрено на примере дифракции электронов. Пусть поток электронов проходит через узкую щель шириной Δx, расположенную перпендикулярно направлению их движения. Так как электроны обладают волновыми свойствами, то при их прохождении через щель, размер которой сравним с длиной волны де Бройля λ электрона, наблюдается дифракция. При этом точность в определении координаты электрона не может быть больше длины волны излучения: . В этот же момент вследствие дифракции электроны отклоняются от первоначального направления, следовательно, появляется неопределенность в значении составляющей импульса Δp_x вдоль оси X порядка импульса фотона: , что и составит погрешность в определении его импульса. Следовательно,

.

(5.11)

Это соотношение носит название: «соотношения неопределенностей Гейзенберга».

То же место имеет и для других координат, так что

.

(5.12)

Формулы (5.12) также являются соотношениями неопределенности, показывающие, что координаты x, y, z и проекций p_x, p_y, p_z ее импульса на соответствующие оси не имеют одновременно значения, равных x и p_x, y и p_y, z и p_z. Их значения определены лишь с некоторой степенью точностью.

В квантовой теории рассматривается также соотношение неопределенностей для энергии E и времени t, т.е. неопределенности этих величин удовлетворяют условию

,

(5.13)

где ΔE – неопределенность энергии некоторого состояния системы, Δt – промежуток времени, в течение которого оно существует. Следовательно, система, имеющая среднее время жизни Δt, не может быть охарактеризована определенным значением энергии.

ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ

5.1. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц.

5.2. Длина волны де Бройля.

5.3. Длина волны для частицы с массой m, движущейся со скоростью υ.

5.4.Связь между энергией W свободной частицы и частотой ν волн де Бройля.

5.5. Определение свободной частицы.

5.6. Фазовая скорость волн де Бройля υ << c.

5.7. Фазовая скорость волн де Бройля υ >> c.

5.8. Групповая скорость волн де Бройля.

5.9. Волновая функция простейшей монохроматической волны.

5.10. Волновой пакет.

5.11. Соотношения неопределенностей Гейзенберга для координат.

5.12. Соотношение неопределенностей Гейзенберга для энергии

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА».

1. Записать соотношения неопределенностей Гейзенберга для координат.

2. Записать дополнительные уравнения, позволяющие определить неизвестные величины.

3. Решить полученную систему уравнений.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА».

Задача 5.1. Кинетическая энергия электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношения неопределенностей, оценить минимальные линейные размеры атома.

Дано: Т=10 эВ	Решение: Согласно уравнению (5.11), соотношение неопределенностей для координаты и импульса имеет вид: . (1)
lmin - ?	Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы.

Пусть атом имеет линейные размеры l, тогда электрон атома будет находится где – то в пределах области с неопределенностью

.

(2)

Тогда соотношение неопределенностей с учетом (23) примет вид:

,

откуда

.

(3)

Неопределенность импульса Δp_x не должна превышать значения самого импульса p_x , т.е .

Импульс p_x связан с кинетической энергией Т соотношением

.

(4)

Подставляя уравнение (4) в (3), получим

.

Вычисления:

.

Ответ: l_min = 124 нм.

Задача 5.2. Среднее время жизни возбужденных состояний атома составляет 10 нс. Вычислить естественную ширину спектральной линии , соответствующую переходу между возбужденными уровнями атома.

Дано: τ =10 -8 с λ = 7 ·10-7 м	Решение: Согласно соотношению неопределенности Гейзенберга для энергии . (1)
Δλ - ?	При переходе электрона из одного стационарного состояния в другое излучается (или поглощается) энергия, равная
		(2)

Из (2) следует, что неопределенность длины волны излучения связана с неопределенностью энергии уровней атома соотношением

.

(3)

Поскольку Δt не превышает среднее время жизни τ возбужденного состояния атома, минимальная неопределенность энергии возбужденных уровней, согласно(1), равна

.

(4)

Из (3) с учетом (4) найдем минимальную неопределенность длины волны излучения, которая называется естественной шириной спектральной линии

.

(5)

Если одно из состояний, между которыми совершается переход, является основным, то

,

(6)

поскольку для основного состояния τ = ∞. Для возбужденного состояний с одинаковым временем жизни имеем

,

Вычисления:

( м )

Ответ: м.
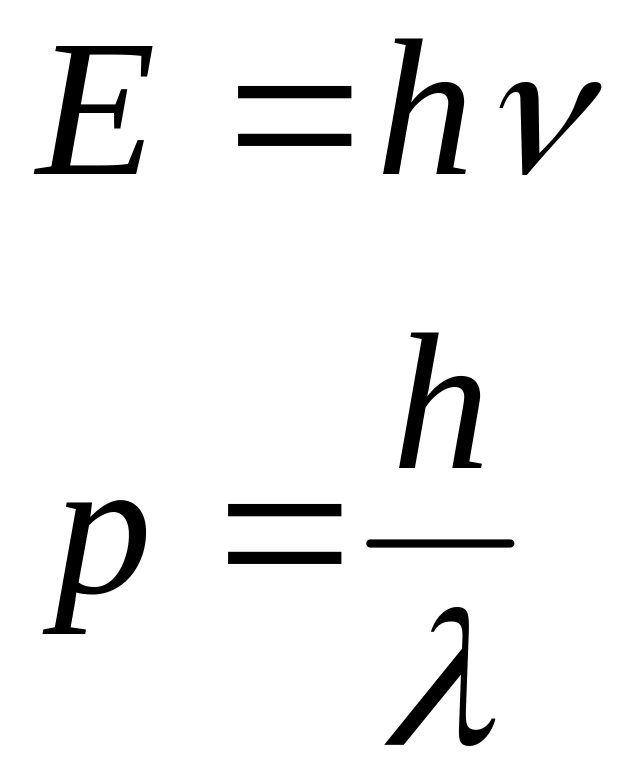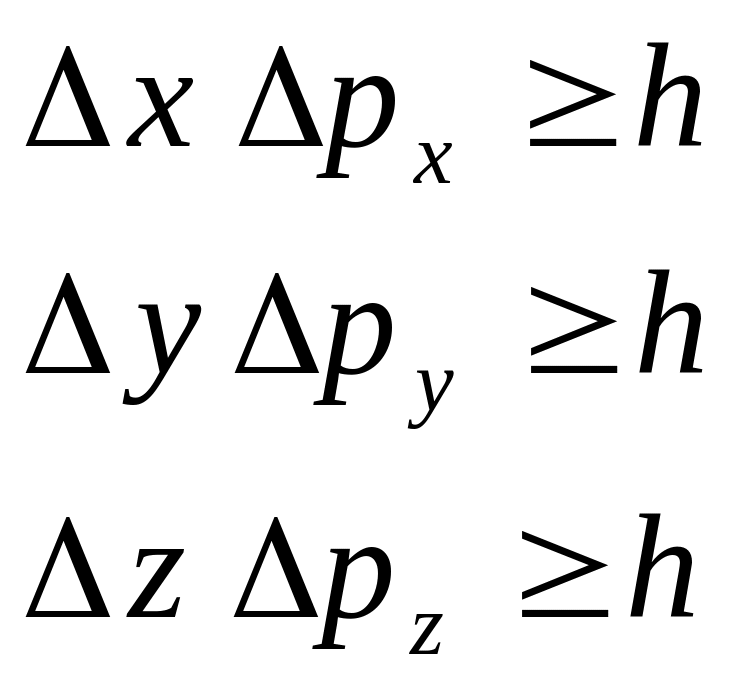