Задачи для самостоятельного решения

5.1. При каких значениях кинетической энергии Т электрона ошибка в определении дебройлевской длины волны по релятивистской формуле не превышает 10%?

(Ответ: Дж)

5.2. Оцените с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R=0,05 нм.

(Ответ: Дж)

5.3. Параллельный пучок моноэнергетических электронов падает нормально на диафрагму в виде узкой прямоугольной щели, ширина которой a=0,06 мкм. Определите скорость этих электронов, если, известно, что на экране, отстоящем от щели на расстоянии l=40 мм, ширина центрального дифракционного максимума b=10 мкм.

(Ответ: Дж)

5.4. Вычислить наиболее вероятную дебройлевскую длину волны молекул азота, содержащихся в воздухе при комнатной температуре.

(Ответ: м)

5.5. Определите длину волны де Бройля для нейтрона, движущегося со средней квадратичной скоростью при Т=290 К.

(Ответ: м)

5.6. Оценить относительную неопределенность импульса движущейся частицы, если допустить, что неопределенность ее координаты равна длине волны де Бройля.

(Ответ: )

5.7. α – частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия α - частицы MэВ.

(Ответ: м)

5.8. Среднее время жизни атома в возбужденном состоянии составляет с. При переходе атома в нормальное состояние испускается фотон, средняя длина волны которого равна нм. Оценить ширину излучаемой спектральной линии, если не происходит ее уширения за счет других процессов.

(Ответ: м)

5.9. Моноэнергетический пучок электронов высвечивает в центре экрана электронно-лучевой трубки пятно, радиусом см. Пользуясь соотношением неопределенностей, найти, во сколько раз неопределенность Δx координаты электрона на экране в направлении, перпендикулярном оси трубки, меньше размера r пятна. Длину L электронно-лучевой трубки принять равной 0,50 м, а ускоряющее электрон напряжение кВ.

(Ответ: )

5.10. Электрон находится в прямоугольном потенциальном ящике с непроницаемыми стенками. Ширина ящика l=0,2 нм, энергия электрона в ящике Е=37,8 эВ. Определите номер n энергетического уровня и модуль волнового вектора k.

(Ответ: м^-1)

6. Квантовые состояния. Уравнения шредингера. Краткая теория

Для описания состояния микрообъекта в квантовой механике вводят функцию (x, y, z, t), называемую волновой функцией (или пси-функцией). С помощью волновой функции (x, y, z, t) в квантовой механике могут быть вычислены средние значения физических величин, который характеризует данный объект, находящийся в состоянии, описываемом волновой функцией . Например, среднее расстояние ‹ r › электрона от ядра вычисляется по формуле

,

(6.1)

где интегрирование производится по всему бесконечному пространству, т.е. по координатам x,y,z от -∞ до +∞.

Физический смысл имеет не сама функция , а квадрат ее модуля. Величина имеет смысл плотности вероятности:

,

(6.2)

где - вероятность обнаружения частицы в момент времени t в элементарном объеме dV.

Вероятность dw того, что частица находится в элементе объема dV, равняется произведению и элемента объема dV:

.

(6.3)

Величина определяет интенсивность волн де Бройля. Волновая функция должна удовлетворять условию нормировки вероятностей:

,

(6.4)

где тройной интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от - до . Это означает, что пребывание частицы где-либо в пространстве есть достоверное событие и его вероятность должна быть равна единице.

Основное уравнение квантовой механики было получено Э. Шредингером. Справедливость уравнения Шредингера доказывается тем, что выводы квантовой механики, полученные с помощью этого уравнения в атомной и ядерной физике, находятся в согласии с экспериментом. Уравнение Шредингера имеет вид:

,

(6.5)

где m – масса частицы; U(x,y,z,t) – потенциальная энергия частицы в силовом поле, где частица движется; - оператор Лапласа;

 = (x, y, z, t) – искомая волновая функция частицы; - мнимая единица.

Уравнение (6.5) справедливо для любой частицы, движущейся со скоростью . Уравнение Шредингера дополняется важными условиями, которые накладываются на функцию  = (x, y, z, t) – условия регулярности:

1. функция  должна быть конечной, непрерывной и однозначной;

2. производные 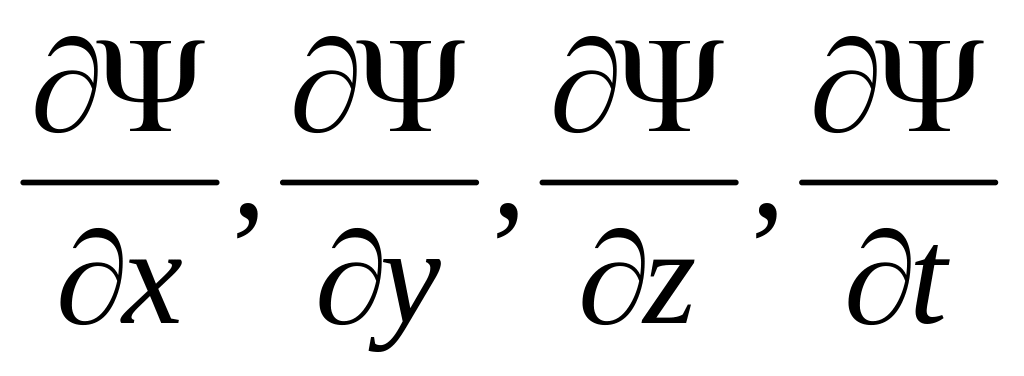должны быть непрерывны;

3. функции должна быть интегрируема, т.е. интеграл

(6.6)

должен быть конечным. В простейших случаях третье условие сводится к условию нормировки вероятности (6.4).

Уравнение (6.5) часто называют временным уравнением Шредингера, так как оно содержит производную от функции  по времени. Однако для большего числа физических явлений, происходящих в микромире, например для описания поведения электрона в атоме, важно уметь находить стационарные решения уравнения Шредингера, не содержащие времени. Для решения этой задачи нужно получить уравнение Шредингера, в котором исключена зависимость  от времени. Оно имеет смысл для тех задач, в которых потенциальная энергия U не зависит от времени: U(x, y, z), т.е.

,

(6.7)

где Е – полная энергия частицы, которая в случае стационарного поля остается постоянной. Уравнение (6.7) называют стационарным уравнением Шредингера. Функции , удовлетворяющие уравнению Шредингера при данном значении U, называют собственными функциями. Значения Е, при которых существуют решения уравнения Шредингера (6.7), называются собственными значениями энергии.

Совокупность собственных значений энергии называется спектром величины. Если совокупность образует дискретную последовательность, спектр называется дискретным. Если собственные значения энергии образуют непрерывную последовательность, спектр называют непрерывным или сплошным. В случае дискретного спектра собственные значения и собственные функции можно пронумеровать:

.

(6.8)

Таким образом, квантование энергии получается из основных положений квантовой механики без каких-либо дополнительных предположений.

1) Рассмотрим пример нахождения собственных значений энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме (рис.6.1).

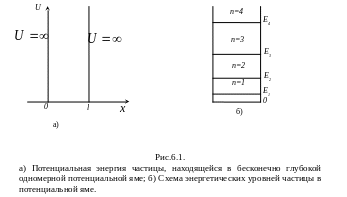Предположим, что частица может двигаться только вдоль оси ОХ. Пусть движение ограничено непроницаемыми для частицы стенками: х_min=0 и x_max=l. Потенциальная энергия U имеет в этом случае следующий вид (рис.6.1, а): она равна нулю при и обращается в бесконечность при x<0 и x>l. Поскольку пси-функция зависит только от координаты x, уравнение Шредингера будет иметь следующий вид:

.

(6.9)

За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Соответственно и функция  за пределами ямы равна нулю. Из условия непрерывности следует, что  должна быть равна нулю и на границах ямы, т.е.

,

(6.10)

В области, где  не равна тождественно нулю, уравнение Шредингера имеет вид:

.

(6.11)

Решение этого уравнения имеет вид:

,

(6.12)

где - волновое число волны де Бройля для электрона, находящегося внутри потенциальной ямы.

Из условия (0)=0 получаем, что

(6.13)

что возможно лишь в случае, если

(n=1,2,3,…),

(6.14)

где n – главное квантовое число.

Тогда собственные значения энергии частицы, находящейся в потенциальной яме:

, (n=1,2,3,…)

(6.15)

т.е. спектр энергии является дискретным. На рис.(6.1.,б) представлена схема энергетических уровней.

Разность энергий двух соседних уровней равна

.

(6.16)

Собственные функции имеют вид:

,

(6.17)

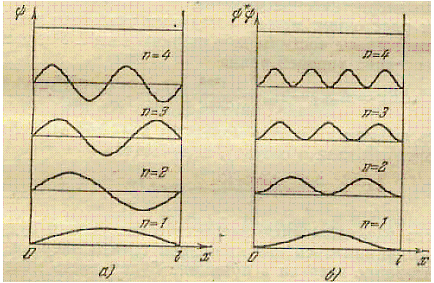
Рис.6.2

Графики собственных функций (а) и плотности вероятности обнаружения частицы на различных расстояниях от стенок ямы.

Графики собственных функций изображены на рис. 6.2 а). На рис. 6.2 б) дана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы. Из графиков следует, что в состоянии с n=2 частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы.

В квантовой механике большую роль играет понятие оператора. Под оператором подразумевают правило, посредством которого одной функции  сопоставляется другая функция f:

,

(6.18)

где - символическое обозначение оператора. Под символом оператора скрывается совокупность действий, с помощью которых одному множеству чисел сопоставляется другое множество чисел.

В квантовой механике другим динамическим переменным также сопоставляются операторы. Соответственно рассматривают операторы координат, импульса, момента импульса и т.д.

Применительно к моменту импульса в квантовой механике вводятся четыре оператора: оператор квадрата момента и три оператора проекции момента на оси координат: 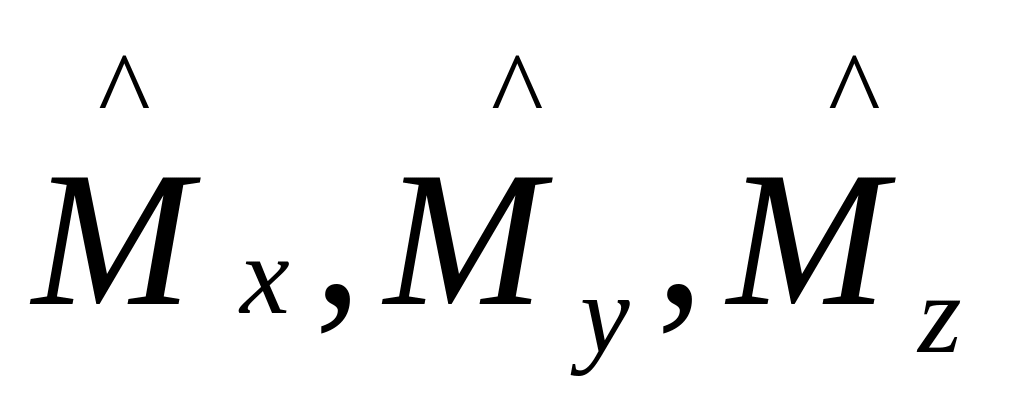. Одновременно могут иметь определенные значения только квадрат момента и одна из проекций момента на координатные оси. Две другие проекции оказываются неопределенными, т.е. не имеют определенного направления и, следовательно, не могут быть изображены, как в классической механике, с помощью направленного отрезка прямой.

Собственные значения оператора квадрата момента импульса равны

(l=0,1,2,….)

(6.19)

где l-квантовое число, называемое азимутальным.

Модуль момента импульса может иметь лишь дискретные значения, определяемые формулой

, (l=0,1,2,….)

(6.20)

Оператор проекции момента импульса на ось z

, (m=0,1,2,….)

(6.21)

где m – магнитное квантовое число.

Момент импульса системы, состоящей из нескольких микрочастиц, равен сумме моментов отдельных частиц. Суммарный момент, как и всякий момент, определяется

,

(6.22)

где l – азимутальное квантовое число результирующего момента. В случае системы, состоящей из двух частиц, число l может иметь значения:

(6.23)

Одним из основных положений квантовой механики является принцип суперпозиции состояний. Суть этого принципа заключается в следующем. Пусть некоторая квантомеханическая система может находиться как в состоянии ^/, так и в состоянии ^//. Тогда существует состояние системы, описываемое функцией

(6.24)

где с^/ и с^// - произвольные комплексные числа. Таким образом, согласно принципу суперпозиции состояний пси-функцию любого состояния можно разложить по собственным функциям этой величины, т.е. представить в виде

,

(6.25)

где c_n – не зависящие от координат, в общем, комплексные числа.

2) Пусть частица, движущая слева направо, встречает на своем пути потенциальный барьер высотой U₀ и шириной l (рис. 6.3).

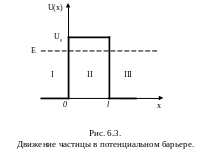
Если энергия частицы больше высоты барьера (E > U₀), то частица беспрепятственно проходит над барьером (на участке лишь уменьшается скорость частицы, но затем при x>1 снова принимает первоначальное значение). Если E меньше U₀ (рис.6.3), то частица должна отражаться от барьера и полететь в обратную сторону; сквозь барьер частица проникнуть не может. Но согласно квантовой механике при E < U₀ имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области x>l. В этом случае уравнение Шредингера будет иметь вид

(6.26)

Общее решение уравнений для частицы, движущейся в потенциальном барьере, имеет следующий вид

(6.27)

где .

Явление прохождения («просачивания») частиц сквозь потенциальные барьеры называется туннельным эффектом. Для описания туннельного эффекта вводится понятие прозрачности D потенциального барьера. Прозрачностью (коэффициентом прозрачности) потенциального барьера называется величина равная отношению интенсивности I_прох волны, прошедшей сквозь барьер и интенсивности I_пад падающей на барьер волны

.

(6.28)

Эту величину можно рассматривать как вероятность прохождения волн де Бройля сквозь потенциальный барьер, или, что то же самое, как вероятность просачивания частицы, описываемой волнами де Бройля, сквозь потенциальный барьер.

Коэффициент отражения R частицы от барьера:

.

(6.29)

В случае прямоугольного потенциального барьера с высотой U₀ и шириной L прозрачность D выражается формулой

,

(6.30)

где D₀ – постоянный коэффициент, близкий к единице, m – масса частицы, Е – ее полная энергия, L – ширина прямоугольного потенциального барьера, U₀ – высота потенциального барьера. Для прямоугольного барьера величину параметра . С параметром a связана эффективная глубина Δx, на которую частица может проникнуть в запрещенную область внутри барьера:

.

(6.31)

3) Линейным осциллятором называется частица с массой m, которая движется вдоль некоторой оси под действием квазиупругой силы F, пропорциональной отклонению x частицы от положения равновесия:

,

(6.32)

где k – коэффициент квазиупругой силы, связанной с массой m частицы и собственной циклической частоты ее колебаний формулой .

П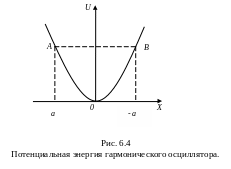 отенциальная энергия гармонического осциллятора изображена на рис. 6.4. В точках А и В кинетическая энергия осциллятора равна нулю и вся энергия переходит в потенциальную энергию осциллятора. Эти точки соответствуют значениям координат , где а – амплитуда колебаний осциллятора. В квантовой механике задача о колебаниях линейного гармонического осциллятора решается с помощью стационарного уравнения Шредингера. Для линейного гармонического осциллятора оно имеет вид

(6.33)

Данное уравнение имеет конечные, однозначные и непрерывные решения при значениях параметра E, равных

(n = 0,1,2,…).

(6.34)

На рис. 6.5. дана схема энергетических уровней гармонического осциллятора. Уровни энергии гармонического осциллятора являются эквидистантными, т.е. отстоящими друг от друга на одинаковое расстояние. Наименьшее возможное значение энергии равно называется нулевой энергией. Существование нулевой энергии подтверждается экспериментами по изучению рассеяния света кристаллами при низких температурах.

Квантовая механика позволяет вычислить вероятность различных переходов квантовой системы из одного состояния в другое. Для гармонического осциллятора возможны лишь переходы между соседними уровнями. При таких переходах квантовое число n изменяется на единицу:

.

(6.35)

Условия (6.35), накладываемые на изменения квантовых чисел при переходах системы из одного состояния в другое, называются правилами отбора.