2 .2.2. Пересечение множеств

Под пересечением множеств и будем понимать множество, обозначаемое и состоящее из тех и только тех элементов, которые обладают одновременно и свойством и свойством . Диаграмма Эйлера пересечения множеств имеет вид, изображённый на рис. 2.3.

Высказывательная форма операции пересечения множеств имеет вид:

.

Или в другой форме: . Для геометрической интерпретации операции пересечения множеств в виде диаграммы Венна будем рассуждать аналогично операции объединения: истинность высказывания левой части выражения должна повлечь истинность правой части .

Конъюнкция, стоящая в правой части выражения будет истинной, если будут истинными оба высказывания и . Истинность этих высказываний геометрически интерпретируется точками и на рис. 2.3. В связи с этим диаграмма Эйлера операции пересечения имеет вид, представленный на рис. 2.3.

Рис. 2.3. Диаграмма Эйлера операции пересечения множеств

Операция пересечения может быть выполнена над множествами, число которых больше двух:

.

Пример 2.2

В качестве исходных множеств рассмотрим множества из предыдущего примера:

и .

Пересечение множеств и представляет собой следующее множество:

.

2.2.3. Разность множеств

Под разностью множеств и будем понимать множество, обозначаемое и состоящее из тех и только тех элементов, которые обладают свойством , но не обладают свойством . Диаграмма Эйлера пересечения множеств имеет вид, изображённый на рис. 2.4. Высказывательная форма операции разности множеств имеет вид:

.

Для построения диаграммы Эйлера операции разности множеств рассмотрим соотношение: . Истинность высказывания должна повлечь истинность сложного высказывания, представляющая собой конъюнкцию высказываний и . Условие истинности конъюнкции и определяет геометрическую интерпретацию разности множеств в виде диаграммы Эйлера (рис. 2.4).

Рис. 2.4.Диаграмма Эйлера операции разности множеств

Пример 2.3

Выполним операции разности и для множеств из предыдущих примеров и :

, .

2.2.4. Дополнение множеств

Дополнением множества называется множество, обозначаемое , элементы которого не обладают свойством .

Диаграмма Эйлера дополнения множества имеет вид, изображённый на рис. 2.5.

Высказывательная форма операции дополнения множеств имеет вид:

.

Рис. 2.5. Диаграмма Эйлера операции дополнения множеств

Пример 2.4

Пусть множество натуральных чисел, не превосходящих 200. Тогда множество натуральных чисел, превосходящих 200.

2.2.5. Симметрическая разность

Симметрическая разность двух множеств и определяется как или в форме соотношения .

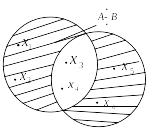
Рис. 2.6. Диаграмма Эйлера операции симметрической

разности множеств

Истинность правой части высказывания должна имплицировать истинность левой части , представляющей собой дизъюнкцию высказываний и . На основании рассуждений, аналогичных рассматриваемым ранее операциям, получим диаграмму Эйлера симметрической разности, представленной на рис. 2.6.

Пример 2.5

Если , , то .

2.2.6. Разбиения и покрытия множеств

Рассмотрим семейство подмножеств множества , , . Семейство называется покрытием множества , если каждый элемент из множества принадлежит хотя бы одному из множеств :

.

Семейство называется дизъюнктивным, если выполняются следующие свойства: , при . Дизьюнктивное покрытие называется разбиением множества .

2.3. Соотношения между множествами

Между множествами могут быть следующие соотношения: строгого включения, нестрогого включения, равенства.

Введём следующие обозначения:

отношение нестрогого включения;

отношение строгого включения;

«=» – отношение равенства;

тогда и только тогда;

квантор общности;

квантор существования.

Множество нестрого включено в множество тогда и только тогда, когда для любого элемента из множества следует его принадлежность к множеству . Высказывательная форма нестрогого включения множеств имеет вид: .

Диаграммы Венна нестрогого включения множеств приведены на рис. 2.7.

а) б)

Рис. 2.7. Диаграммы Венна нестрогого включения

При нестрогом вкючении в множестве могут как присутствовать (рис. 2.7.а), так и отсутствовать (рис. 2.7.б) элементы множества В, не принадлежащие множествуА.

Множество строго включено в множество тогда и только тогда, кода, как и в случае нестрогого включения, для любого элемента из множества следует его принадлежность к множеству . Отличие состоит в том, что в множестве обязательно должны присутствовать элементы, не принадлежащие множеству . Высказывательная форма отношения строгого включения имеет вид:

.

Диаграмма Эйлера отношения строгого включения приведена на рис. 2.8.

Два множества и будем считать равными, если для них справедлива следующая высказывательная форма

.

Диаграмма Венна отношения равенства двух множеств приведена на рис. 2.9.

Рис. 2.8. Диаграмма Эйлера отношения строгого включения

Рис. 2.9. Диаграмма Венна отношения равенства множеств

Приведённая высказывательная форма является критерием равенства множеств. В соответствии с этим критерием для любого произвольного меожества порядок следования его элементов не играет никакой роли:

.

Кроме того, добавление во множестве любого количества одинаковых элементов или их удаление не изменяет множества.

.