Вопросы к разделу 1

1. Дайте определение функции алгебры логики.

2. Что называется областью определения функции алгебры логики?

3. Сколько различных наборов значений аргументов можно составить для функции алгебры логики, зависящей от переменных?

4. Дать определение функции алгебры логики, существенно зависящей от аргумента.

5. Дать определение функции алгебры логики, несущественно зависящей от аргумента.

6. Сколько функций алгебры логики, зависящей от аргументов, можно составить?

7. Составьте таблицы истинности элементарных функций алгебры логики.

8. Перечислите свойства дизъюнкции, конъюнкции, отрицания.

9. Запишите свойства функций «Штрих Шеффера» и «Вебба».

10. Перечислите свойства функции сложения по модулю 2.

2. Теория множеств и отношений

2.1. Множества. Способы задания множеств

Начало теории множеств было положено в ХIХ веке работами Больцано, Дюбуа, Реймона, Дедекинда, посвящёнными числовым множествам и множествам функций. Но основателем теории множеств является Георг Кантор, рассмотревший в своих работах множества произвольных элементов. В 1971-1883 гг. он опубликовал научные работы, в которых изложено практически всё современное содержание теории кардинальных чисел, порядковых чисел и теории вполне упорядоченных множеств. Хотя основные положения и обобщения изложенной теории содержали немало противоречий, позволяющих строить антиномии теории множеств, это был, всё же, очень важный шаг. Эти противоречия были преодолены Цермело посредством работ, опубликованных в 1904-1908 гг. и содержащих первую систему аксиом теории множеств. Этих аксиом оказалось достаточно, чтобы получить важные для математики научные результаты, не позволяющие строить известные антиномии. Тесная связь между теорией множеств и философией математики породило немало дискуссий о природе антиномий и аксиоматизации теории множеств. Фундаментальные проблемы философии математики, такие как понятие существования в математике, аксиоматические версии описания действительности, необходимость доказательств непротиворечивости и средства, допустимые в таких доказательствах, нигде не были выяснены лучше, чем в этих дискуссиях. Недоверие к теории множеств прекратилось и основные положения вновь созданной теории стали повсеместно использоваться во всех областях математики.

Основным понятием теории множеств является множество и отношение быть элементом. Это понятие по мере развития теории претерпело значительные изменения. В начальный период развития теории множеств, во времена так называемой «наивной» теории множеств, пользовались интуитивным понятием множества. В рамках этого понятия слово «множество» имело неопределённое значение. В частности, такую позицию занимал создатель теории множеств Георг Кантор.²

Но такое положение долго не продержалось.

Под множеством будем понимать совокупность элементов, объединённых некоторым признаком или свойством. Например, множество журналов, множество статей в журнале, множество студентов в группе, на факультете и т.д. Принадлежность некоторого элемента множеству будем записывать как , а непринадлежность – . Множество можно задать тремя способами. Первый способ – перечисление элементов. В этом случае обозначения элементов заключают в фигурные скобки в виде записи или или . Второй способ – использование характеристического предиката (характеристического свойства). Характеристический предикат – это некоторое условие в виде логического утверждения, которое возвращает логическое значение из множества {0,1}. Во втором случае используется запись , означающая, что множество состоит из элементов, обладающих свойством , или , означающая, что множество состоит из тех и только тех элементов натурального ряда чисел, которые больше 100. Характеристическое свойство записывается после знака «/». В первом случае в качестве характеристического свойства выступает указанная для этого свойства порождающая процедура . Эта процедура описывает способ получения элементов нового множества из уже полученных элементов или каких-либо объектов. Таким образом, запись означает, что множество состоит из элементов, обладающих признаком . В качестве этого признака может быть использовано уравнение: . Это означает, что множество состоит из корней уравнения . Таким образом, если для данного элемента выполняется условие, то он принадлежит множеству, в противном случае не принадлежит. Третий способ – использование порождающей процедуры, которая в случае её активизации порождает некоторые объекты, являющиеся элементами определяемого множества: . Перечислением можно задавать только конечные множества (определение конечного множества приведено ниже).

Множество, не содержащее ни одного элемента, называется пустым. Пустое множество обозначается .

Множество, состоящее из всех возможных элементов, обладающих заданным признаком, называется универсальным и обозначается как . Примером универсального множества может быть множество планет Солнечной системы .

Понятие универсального множества чётко не определено, т.е. не корректно. Одно универсальное множество можно включить в другое множество, которое также будет универсальным.

Множество называется конечным, если число его элементов конечно. Множество называется бесконечным, если количество его элементов бесконечно.

Обычно множества обозначают прописными буквами латинского алфавита, а элементы множеств – строчными буквами. Множества геометрически представляются с помощью кругов Эйлера (диаграмм Венна) (рис. 2.1.). В диаграммах Венна элементы множества изображаются точками внутри круга, если они принадлежат множеству ( ), и точками вне круга, если они не принадлежат этому множеству ( ).

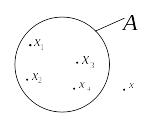
Рис. 2.1. Диаграмма Эйлера представления множеств

Множества, как объекты, в свою очередь могут быть элементами других множеств. Множество, элементами которого являются множества, называются семействами или классами.