
- •Е.Д. Стрельцова, в.С. Стрельцов моделирование дискретных систем Учебно-методическое пособие по дисциплине «Дискретная математика»
- •2. Теория множеств и отношений………………………………….20
- •Введение
- •1. Функции алгебры логики
- •1.1. Основные понятия
- •Пример функции алгебры логики , заданной таблицей
- •1.2. Алгоритм нахождения фиктивных аргументов.
- •1.3. Элементарные функции алгебры логики
- •Функции алгебры логики, зависящие от одного аргумента
- •Вопросы к разделу 1
- •2. Теория множеств и отношений
- •2.1. Множества. Способы задания множеств
- •2.2. Основные операции над множествами
- •2.2.1. Объединение множеств
- •2 .2.2. Пересечение множеств
- •2.2.3. Разность множеств
- •2.2.4. Дополнение множеств
- •2.4. Свойства операций над множествами
- •2.5. Упорядоченные множества
- •2.6. Прямое (декартово) произведение множеств
- •2.7. Степень множеств
- •2.8. Сечение и проекция
- •Декартово произведение
- •2.9. Соответствия
- •2.10. Композиция соответствий.
- •2.11. Отображения
- •2.12. Виды отображений. Функциональное отображение (функция)
- •2.13. Функционалы
- •2.14. Операторы
- •2.15. Линейные операторы
- •Отношение «Читает лекции по…»
- •Отношение «Посещать лекции»
- •2.20. Бинарные отношения
- •2.20.1. Матричный способ задания отношений
- •2.20.2. Задание отношений в виде графа
- •2.20.3. Задание отношений с помощью фактор множества
- •2.21. Свойства бинарных отношений
- •2.22. Отношение эквивалентности
- •2.23. Отношение порядка
- •2.24. Изоморфизм отношений
- •2.26. Операции над бинарными отношениями
- •2.26.1. Объединение отношений
- •2.26.2. Пересечение отношений
- •2.26.3. Разность отношений
- •2.26.4. Включение отношений
- •2.26.5. Переход к обратному отношению
- •2.26.6. Произведение отношений
- •2.26.7. Транзитивное замыкание
- •Вопросы к разделу № 2
- •3. Алгебраические системы
- •3.1. Понятие алгебраической системы
- •3.1. Морфизм алгебраических систем
- •3.3. Автоморфизмы
- •3.4. Виды универсальных алгебр
- •3.4.1. Полугруппы. Моноиды
- •3.4.2. Морфизм групп
- •3.4.3. Свойства морфизма групп
- •3.4.4. Кольцо
- •Вопросы к разделу №3
- •4. Практикум к решению задач Основные обозначения
- •4.1. Операции над множествами
- •Разностью множеств а и в называется множество
- •Симметрической разностью множеств а и в называется множество
- •Пустым множеством называется множество, не имеющее ни одного элемента.
- •Задачи и упражнения
- •На основании (14) можно записать
- •По определению объединения
- •Пусть теперь у (ав) (ас) у (ав) у (ас) (у а у в) (у а у с) у а (у в у с)
- •Задачи для самостоятельного решения
- •4.2. Векторное произведение
- •4.3. Соответствие
- •Свойства отношений
- •Список литературы
- •Моделирование дискретных систем
- •3 46428, Г. Новочеркасск, ул. Просвещения, 132
2.13. Функционалы
ФУНКЦИОНАЛ [functional] – переменная величина, заданная на множестве функций, т.е. зависящая от одной или нескольких функций. По другому определению – функция, аргументы которой также представляют собой функции некоторых переменных. Примерами Ф. являются площадь, ограниченная замкнутой кривой заданной длины, работа силового поля вдоль того или иного пути и т.д.
Функциона́л – числовая функция, заданная на векторном пространстве. Функционал берёт в качестве аргумента элемент линейного пространства (вектор) и возвращает в качестве результата скаляр. Довольно часто в роли линейного пространства выступает то или иное пространство функций (непрерывные функции на отрезке, интегрируемые функции на плоскости и т.д. Поэтому, неформально говоря, функционал – это функция от функций, переводящая функцию в число.
Для
разбора понятия функционала рассмотрим
функциональное отображение
![]() ,
в котором множество
представляет собой некоторое множество
функций
,
в котором множество
представляет собой некоторое множество
функций
![]() ,
,
а множество действительных чисел. Такое отображение называется функционалом. Функционал – это множество упорядоченных пар, первый элемент которых представляет собой некоторую функцию, а второй элемент – действительное число:
![]() .
.
Пусть
дан некоторый класс
функций
![]() .
Если каждой функции
.
Если каждой функции
![]() по некоторому закону (правилу) поставлено
в соответствие определенное число
по некоторому закону (правилу) поставлено
в соответствие определенное число
![]() ,
то говорят, что в классе
определен функционал
,
и пишут
,
то говорят, что в классе
определен функционал
,
и пишут
![]() .
Класс
функций
,
на котором определен функционал
.
Класс
функций
,
на котором определен функционал
![]() ,
называется областью задания функционала.
,
называется областью задания функционала.
Пример 2.15.
Пусть
![]() –
совокупность всех непрерывных функций
y(x), заданных
на отрезке [a,b],
и пусть
–
совокупность всех непрерывных функций
y(x), заданных
на отрезке [a,b],
и пусть
 .
(1)
.
(1)
Тогда
есть
функционал от
:
каждой функции
отвечает определенное значение
. Этот функционал геометрически означает
площадь, ограниченную кривой
![]() ,
осью
,
осью
![]() и ординатами
и ординатами
![]() ,
,
![]() .
.
Подставляя
в (1) вместо
конкретные функции, мы будем получать
соответствующие значения
.
Положим для определенности
![]() ,
,
![]() :
:
 ;
;
Если
![]() ,
то
,
то
 ;
;
если
![]() ,
то
,
то
 ;
;
если
 ,
то
,
то
 .
.
Пример 2.16
Пусть
![]() – класс (совокупность) всех непрерывных
функций
,
обладающих непрерывной первой производной
на отрезке [a,b]. Тогда
– класс (совокупность) всех непрерывных
функций
,
обладающих непрерывной первой производной
на отрезке [a,b]. Тогда
 (2)
(2)
будет
функционалом, определенным на этом
классе функций. Функционал (2) геометрически
выражает длину дуги кривой
с концами в точках
![]() и
и
![]() .
.
Например,
если![]() ,
,
![]() ,
,
то
,
,
то
 .
.
Если
 (цепная линия, гиперболический косинус),
(цепная линия, гиперболический косинус),
 ,
то
,
то
 .
.
Пример 2.17
Пусть по прежнему, и пусть
![]() .
.
Ясно,
что
есть функционал, определенный в указанном
классе функций: каждой функции из этого
класса ставится в соответствие
определенной число – значение производной
этой функции в фиксированной точке
![]() .
.
Если,
например,![]() ,
,
![]() и
и
![]() ,
то для
,
то для
![]() имеем:
имеем:
![]() ;
;
для
![]() имеем:
имеем:
![]() ;
;
для
![]() имеем:
имеем:
![]() .
.
Задачи оптимизации формулируются на языке функционалов: найти решение (уравнения, системы уравнений, системы ограничений, системы неравенств, системы включений и т. п.), доставляющее экстремум (минимум, максимум) заданному функционалу.
2.14. Операторы
В информационных системах это правило, переводящее некоторый объект или систему из одного состояния в другое, элемент решения задачи. В качестве оператора, например, может выступать модель, реализующая некоторое преобразование над входными данными.
Рассмотрим
функциональное отображение
![]() ,
где
и
– множества функций:
,
где
и
– множества функций:
![]() ,
,
![]() .
.
В
этом случае отображение
![]() называется оператором.
называется оператором.
Оператор представляет собой множество упорядоченных пар, первый и второй элементы которых представляют собой функции.
Таким образом, под операторами понимают отображение, ставящее в соответствие функции другую функцию («оператор на пространстве функций» звучит лучше, чем «функция от функции»).
![]() .
.
В математике и технике широко применяется условная форма записи операторов, аналогичная алгебраической символике. Такая символика в ряде случаев позволяет избежать сложных преобразований и записывать формулы в простой и удобной форме. Аргументы оператора называются операндами, число операндов называется арностью оператора (например, одинарный, бинарный). Написание операторов можно систематизировать следующим образом:
- префиксная: где первым идёт оператор и операнды следом, например:
![]() ;
;
- постфиксная: если символ оператора следует за операндами, например:
![]() ;
;
- инфиксная: оператор вставляется между операндами, применяется преимущественно с двоичными операторами:
![]() ;
;
- позиционная: знак оператора опускается, оператор присутствует неявно. Чаще всего не пишется оператор произведения (переменных, численного значения на физическую единицу, матриц, композиция функций), например, 3 кг. Такая способность одного оператора действовать над разнородными сущностями достигается перегрузкой операторов;
- подстрочная или надстрочная слева или справа; главным образом используется для операций возведения в степень и выбора элемента вектора по индексу.
Примеры операторов
Оператор,
действующий над пространствами функций
– это правило, согласно которому одна
функция преобразуется в другую.
Преобразование функции
![]() согласно правилу
в другую функцию
согласно правилу
в другую функцию
![]() имеет вид
имеет вид
![]() или, проще,
или, проще,
![]() .
.
Примерами
подобных преобразований – умножение
на число:
![]() ,
дифференцирование
,
дифференцирование
 ,
интегрирование
,
интегрирование
 .
Соответствующие операторы называются
операторами умножения на число,
дифференцирования, интегрирования,
решения дифференциального уравнения
и т. д.
.
Соответствующие операторы называются
операторами умножения на число,
дифференцирования, интегрирования,
решения дифференциального уравнения
и т. д.
Определяя оператор, мы рассматривали только преобразование функции в другую функцию y того же аргумента . Такое сохранение аргумента при определении оператора вовсе не является обязательным: оператор может преобразовывать функцию одного аргумента в функцию другого аргумента, например:
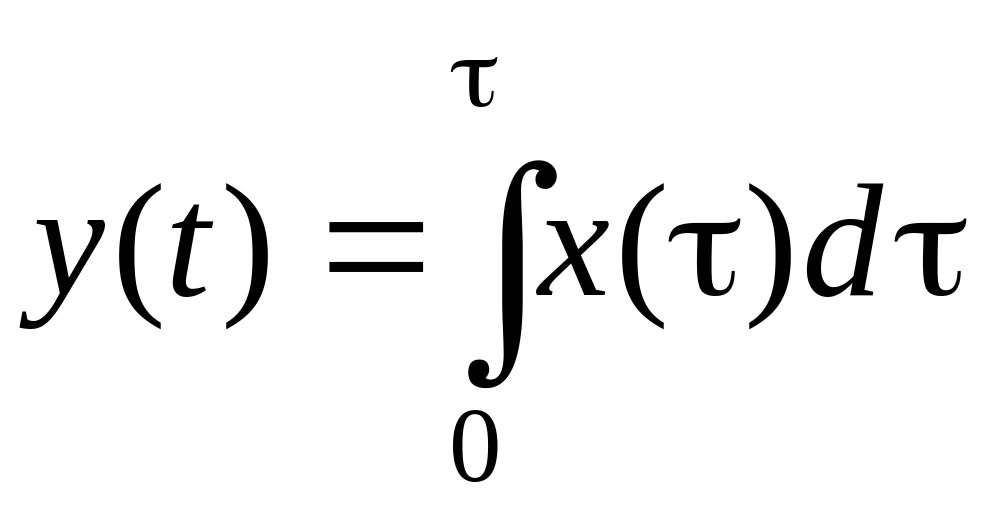 .
.
Отличие оператора от простой суперпозиции функций в данном случае заключается в том, что значение функции y, вообще говоря, в каждой точке зависит не только от , а от значений функции во всех точках .
Еще
в качестве примера оператора можно
привести операцию умножения вектора
длины
на матрицу размером
![]() .
Этот оператор отображает
-мерное
пространство векторов в
-мерное.
.
Этот оператор отображает
-мерное
пространство векторов в
-мерное.
Фундаментальным для практики является класс так называемых линейных операторов. Он также является наиболее исследованным.
