2.22. Отношение эквивалентности
Некоторые элементы множества могут быть рассмотрены как эквивалентные. К эквивалентным элементам отнесём такое подмножество элементов, в котором один элемент может быть заменён другим элементом. В этом случае говорят, что эти элементы находятся друг с другом в отношении эквивалентности.
Пример 2.20
Рассмотрим
множество
.
Если
;
,
,
,
,
то между элементами
существует отношение эквивалентности:
содержать одинаковое число единиц.
Такое же отношение существует и между
элементами
.
Если
на множестве
задать
отношение эквивалентности «иметь
одинаковый знаменатель» и при этом
,
,
,
,
,
то в заданном отношении находятся
элементы
,
а также элементы
.
Отношение эквивалентности обладает следующими свойствами:
- каждый элемент эквивалентен самому себе;
- высказывание относительно эквивалентности между двумя элементами не требует уточнения, какой из элементов рассматривается первым, а какой вторым;
- два элемента, эквивалентных третьему элементу, эквивалентны между собой.
Зададим
на некотором произвольном множестве
бинарное отношение
,
.
Это отношение будем называть отношением
эквивалентности, если оно обладает
следующими свойствами:
- рефлексивности
,
или в инфиксной форме
,
в префиксной форме
,
в постфиксной форме
.
- симметричности
,
или инфиксной форме
,
в префиксной форме
,
в постфиксной форме
;
- транзитивности
,
в
инфиксной форме
,
в
префиксной форме
,
в
постфиксной форме
.
Таким
образом, бинарное отношение
называется отношением эквивалентности,
если оно рефлексивно, симметрично и
транзитивно. Отношение эквивалентности
является подмножеством декартова
произведения
.
Следовательно, элементами отношения
эквивалентности являются упорядоченные
пары:
.
Пример 2.21
Рассмотрим
множество
из
предыдущего примера
,
где
;
,
,
,
и бинарное отношение
,
,
означающие соответственно «иметь
одинаковое число единиц». Тогда
представляет
собой следующее множество упорядоченных
пар:
.
Если
принять
,
,
,
,
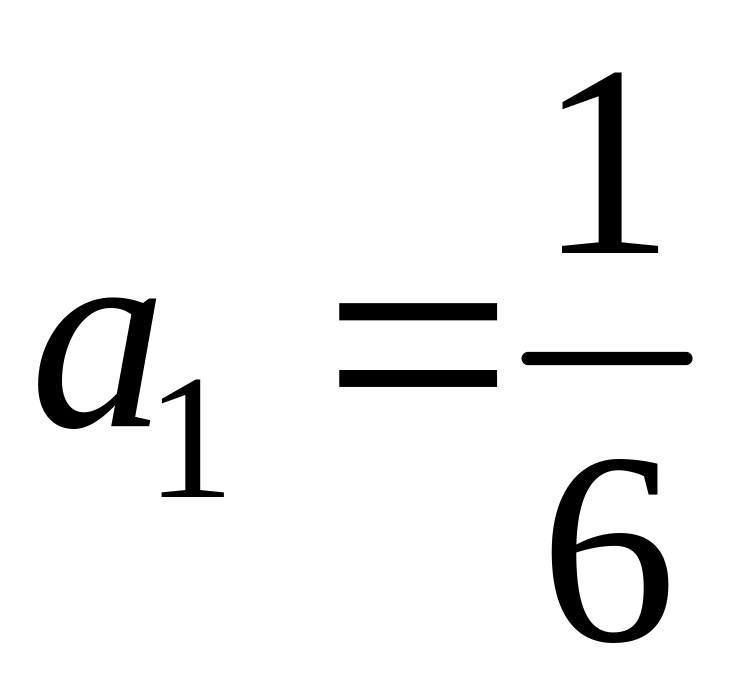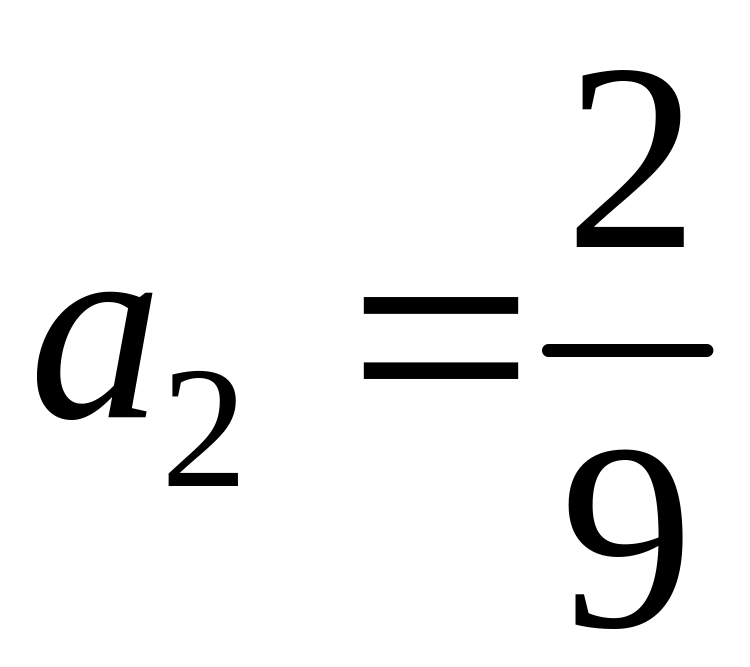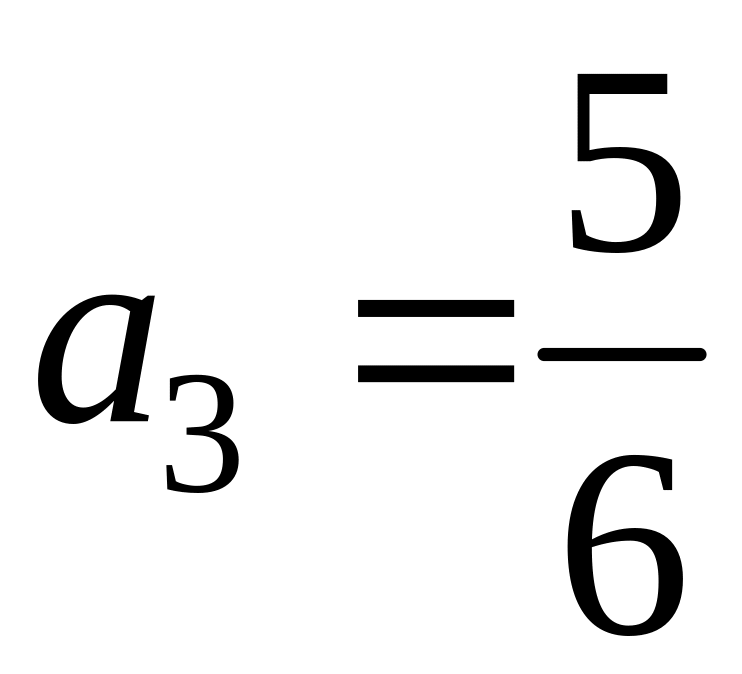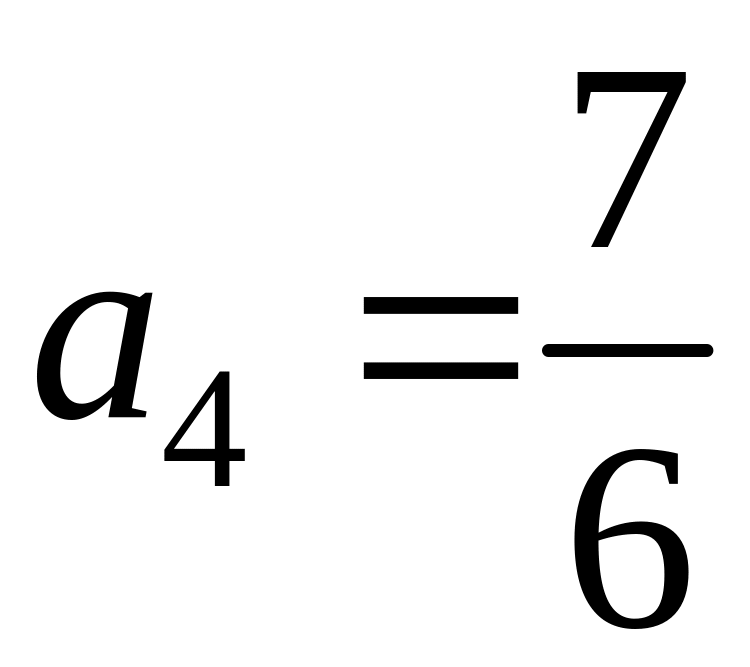и задать на множестве
бинарное отношение
,
,
означающее «иметь одинаковый знаменатель»,
то отношение
представляет собой следующее множество
упорядоченных пар:
.
Теорема 2.1
Любое отношение эквивалентности определяет разбиение множества на попарно непересекающиеся подмножества, т.е. на классы.
Доказательство:
Рассмотрим
любое произвольное множество
.
Перед доказательством теоремы вспомним,
что означает разбить множество
на классы. В соответствии с операцией
разбиения это означает найти такие
множества
,
называемые классами, для которых
справедливо следующее:
-
объединение всех классов
,
составит множество
:
;
-
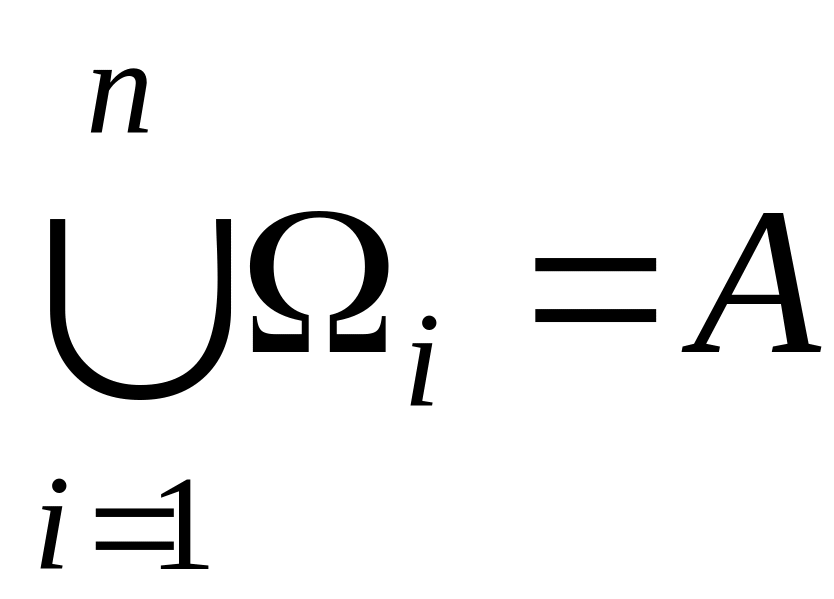пересечение всех классов пусто:
,
.
Если
на множестве
задать отношение эквивалентности
,
то всевозможные сечения (или окрестности
единичного радиуса) образуют классы.
Докажем это. Сначала докажем, что
объединение всех сечений даст множество
.
Запишем высказывательную форму отношения:
.
Возьмём любой произвольный элемент
из множества
:
.
Рассмотрим сечение отношения
элементом
:
.
Образуем
такие сечения для всех элементов
.
Так как
.
Следовательно, каждый элемент множества
будет принадлежать какому-либо сечению.
Тогда можно сделать вывод, что
.
Докажем, что пересечение всех классов
является пустым множеством. Доказательство
будем проводить методом от противного.
Допустим, что сечения отношения
эквивалентности
по некоторым элементам
и
пересекаются, т.е.
.
Тогда в пересечении этих множеств
присутствует хотя бы один элемент
:
.
Очевидно, что
;
и
.
В сечении
рассмотрим некоторый элемент
.
Тогда можно записать
.
Рассмотрим следующие элементы множества
:
,
и
.
Тогда справедливо соотношение:
.
Следовательно
.
Таким образом, отношение эквивалентности находится во взаимосвязи с разбиением множества.
Подмножество элементов, эквивалентных некоторому элементу , называется классом эквивалентности.
Все элементы одного класса эквивалентны между собой и каждый элемент может находиться только в одном классе. Значит, каждому отношению эквивалентности на множестве соответствует некоторое разбиение множества на классы. Необходимым и достаточным условием для того, чтобы некоторое отношение позволяло разбить множество на классы является совокупность свойств рефлексивности, симметричности и транзитивности.