2.7. Степень множеств

Рассмотрим декартово произведение , в котором декартовы сомножители совпадают: . Обозначим каждое из этих множеств через . Тогда декартово произведение представляет собой декартову степень множества :

.

Декартова степень множества с показателем степени представляет собой множество упорядоченных . Высказывательная форма множества имеет вид:

.

Пример 2.9

Рассмотрим множество . Найдём для него вторую декартову степень:

.

Аналогично можно задать множество, представляющее слбой третью декартову степень множества :

.

Если число элементов множества обозначить как , то .

2.8. Сечение и проекция

Сначала разберём понятие проекции. Рассмотрим некоторое множество и . В соответствии с определением элемент представляет собой упорядоченную пару , первый элемент которой принадлежит множеству , а второй – множеству : , . Элемент является проекцией множества на множество и обозначается , а проекцией множества на множество и обозначается .

Рассмотрим множество Е, которое представляет собой подмножество множества : .

Можно говорить о проекции подмножества E на множества и .

Проекцией множества на множество называется множество тех элементов, которые являются проекциями всех элементов множества на множество . Высказывательная форма проекций множества на множества и записывается в виде:

, .

Пример 2.10

Рассмотрим множества и . Множество зададим таблицей 2.1.

Зададим множество методом перечисления его элементов:

.

Тогда если , то , , , .

Таблица 2.1

Декартово произведение

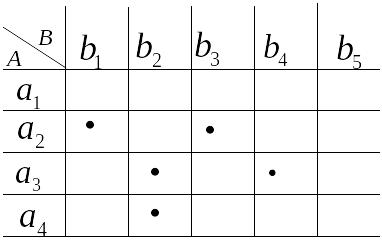
Пример 2.11

Декартово произведение . Если и представляют собой множества действительных чисел, то геометрической интерпретацией множества является множество точек плоскости (рис 2.10.).

Рис. 2.10. Множество для примера 1

Рассмотрим подмножество , представляющее собой некоторую кривую и множество , в свою очередь являющееся подмножеством , . Проекциями множества на множества и являются следующие множества:

, .

Множество может представлять собой декартово произведение множеств, число которых больше двух:

.

Если рассмотреть некоторое подмножество этого множества , то можно говорить о проекции этого множества на множество :

.

Разберём понятие сечения. Рассмотрим некоторый элемент из множества . Тогда сечение множества элементом называется множество элементов из , которые составляют упорядоченную пару из множества :

.

Аналогично можно рассматривать сечение множества элементом : .

Пример 2.12

Рассмотрим множества , и множество , заданное таблицей 2.1. Тогда сечением множества элементом является множество , а сечением множества элементом является множество .

Рассмотрим понятие сечения, когда множество является подмножеством множества

.

Тогда сечение множества элементом представляет собой множество, задаваемое высказывательной формой:

.

Можно говорить о сечении множества более сложным элементом, представляющим собой упорядоченное множество :